正則行列と正規行列(ムーア・ペンローズ逆行列, エルミート行列, ユニタリー行列)
N×Nの正方行列: について考える。
1. 正則行列
以下の命題は同値である。
※ を満たす写像
を、
次行列
に対応する1次変換とする。
- 行列
は正則行列である。
- 行列
に対して、
を満たす逆行列
が存在する
- 行列
に対して、行列式
である。
- 行列
に対して、
である。
- 行列
に対して、すべての固有値が
ではない。
- 行列
に対して、連立1次方程式「
」が唯一解をもつ。
- 行列
に対して、連立1次方程式「
」の解は
のみ。
- 行列
に対して、
の列ベクトル
は一次独立。
- 行列
に対して、
は 「全単射」である。
- 行列
に対して、
は
をみたす。
- 行列
に対して、
は
をみたす。
2. ムーア・ペンローズ逆行列
以下の性質(1)〜(4)を満たす行列を、「行列
に対するムーア・ペンローズ逆行列」という。
(1)
(2)
(3)
(4)
ある行列に対して、(1)を満たす行列
は複数あり、これを「一般逆行列」という。
ある行列に対して、(1)〜(4)を満たす行列
はただ1つに定まり、これを「ムーア・ペンローズ逆行列」という。
また、 と
はエルミート行列である。
3. 正規行列
以下の命題は同値である。
- 行列
は正規行列である。
- 行列
に対して、
が成り立つ。
- 行列
に対して、
は対角化可能である。
※ 随伴行列
一般に、行列 の随伴行列
は、
の「転置行列」を各成分において「複素共軛(実部はそのままで虚部の符号を反転する)」したものとして定義される。
なお、 が複素行列である場合、以下の等式が成り立つ。
さらに、 が実行列である場合、以下の等式が成り立つ。
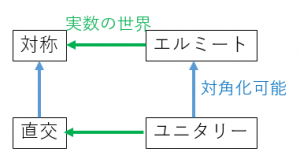
4. エルミート行列とユニタリー行列(複素行列への拡張)
N×Nの複素正方行列: に対して、以下の呼び名が定義される。
- 行列
が「対称行列」である。
- 行列
が「直交行列」である。
- 行列
が「エルミート行列」である。
- 行列
が「ユニタリー行列」である。
ここで、「対称行列」「直交行列」「エルミート行列」「ユニタリー行列」はいずれも正規行列であり、対角化可能となる。
エルミート行列は、対称位置にある成分が互いに複素共役になっている。
多変量ガウス分布についてのベイズ推定(周辺分布, 条件付き分布)
2.ガウス分布の共役性とベイズ推定
◯多変量ガウス分布の周辺分布と条件付き分布
(2a.) の周辺分布 :
(2b.) の条件つき分布 :
(2c.) の周辺分布 :
(2d.) の条件付き分布 :
※ の共分散行列
について、
である。
ここで、ベイズの定理によって(2a.)~(2d.)をまとめると、
より以下の式を得られる。
3. 線形基底関数モデル
3.1 モデルの一般式
「線形基底関数モデル」の一般形は以下の式で表現できる。
を線形基底関数と呼び、これは入力変数
、基底関数
、重みパラメータ
によって表現される。
はベクトルであり、各要素を以下のように表す。
群論入門・写像〜群の定義まで

群論、難しい...。
頭の中でルービックキューブやあみだくじを想像して、なんとか概念を理解したい。
1.写像
1.1 写像に関する諸概念
◯ 写像
集合に対して、集合
の各元をそれぞれ集合
の1つの元に対応させる。
この操作を「から
への写像」といい、以下のように書く。
\begin{align}
f: X→Y
\end{align}
の元
が
の元
に対応しているとき、
を「
による
の写像」といい、以下のように書く。
\begin{align}
b=f(a)
\end{align}
◯ の定義域・終域・値域
写像に対して、集合
を「
の定義域」「
の終域」といい、
の部分集合
を「
の値域」といい「
」と書く。
\begin{align}
f: X→Y\\
(fの定義域)=X\\
(fの終域)=Y\\
(fの値域)=\{f(x) ~|~ x~{\in}~X\}
\end{align}
◯ の像
の部分集合
に対して、以下で示す
の集合を「
による
の像」といい
と書く。
\begin{align}
集合:f(A)~=~\{f(x)~|~x~{\in}~A\}
\end{align}
また、の元
に対して、以下で示す
の元を「
による
の像」といい、
と書く。
\begin{align}
元:f(a)~=~\{f(x)~|~x~=~a\}
\end{align}
◯ の逆像
の部分集合
に対して、以下で示す
の集合を「
による
の逆像」といい
と書く。
\begin{align}
集合:f^{-1}(B)~=~\{x~{\in}~X~|~f(x)~{\in}~B\}
\end{align}
また、の元
に対して、以下で示す
の集合
を「
による
の逆像」といい、
と書く。
\begin{align}
集合:f^{-1}(b)~=~\{x~{\in}~X~|~f(x)=b\}
\end{align}
1.2. 単射・全射・全単射
◯ 単射
集合から集合
への写像
に対して、
上の任意の2つの元
において、
の像が
が成り立つとき、写像
を「
から
への単射」という。
\begin{align}
f: X→Y\\
a~{\neq}~b~{\Rightarrow}~f(a)~{\neq}~f(b)
\end{align}
◯ 全射
集合から集合
への写像
に対して、
の値域が
と一致する時、写像
を「
から
への全射」という。
\begin{align}
f: X→Y\\
\{f(x)~|~x~{\in}~X\}~{\equiv}~Y
\end{align}
◯ 全単射
集合から集合
への写像
に対して、
が「全射かつ単射」である時、写像
を「
から
への全単射」という。
\begin{align}
f: X→Y\\
a~{\neq}~b~{\Rightarrow}~f(a)~{\neq}~f(b)~かつ~\{f(x) ~|~ x~{\in}~X\}~{\equiv}~Y
\end{align}
2.置換
2.1 置換(および互換)に関する諸概念
◯ 集合上の置換
集合から集合
への全単射のうち、とくに
であるものを「集合
上の置換」という。
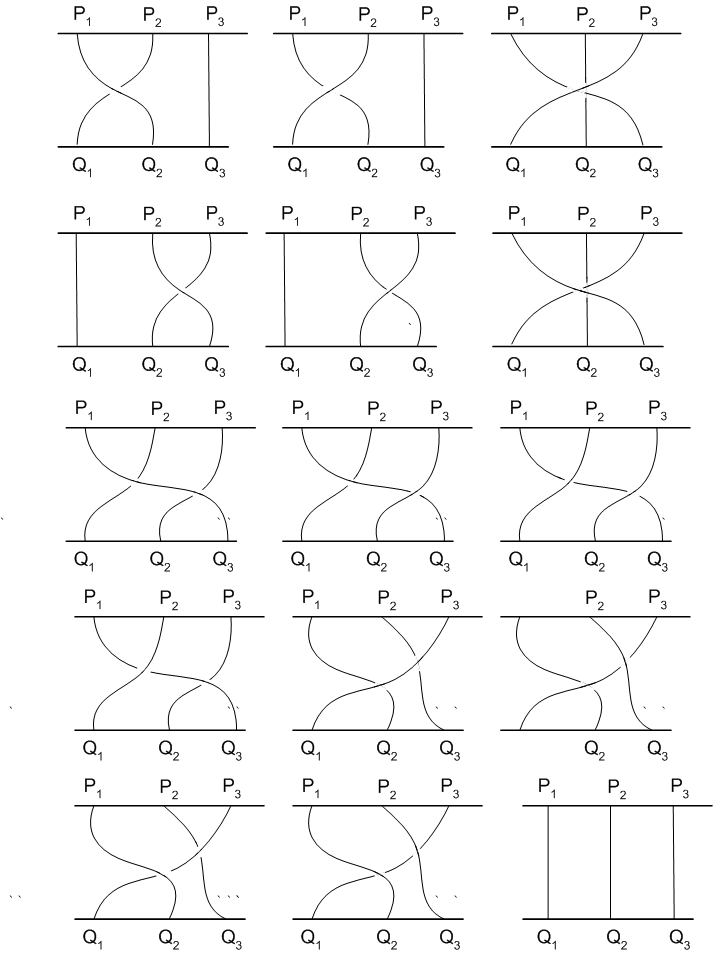
n個の元をもつ有限集合
の置換は以下のように書ける。
\begin{align}
\left(
\begin{array}{ccc}
a_1 & a_2 & a_3 & ... & a_n \\
f(a_1) & f(a_2) & f(a_3) & ... & f(a_n)
\end{array}
\right)
\end{align}
◯ 集合上の互換
集合上の置換のうち、とくに
上の異なる2つの元
の取り替え(=交換)になっているものを「集合
上の互換」といい「
」と書く。
有限集合の互換は以下のように書ける。
\begin{align}
\left(
\begin{array}{ccc}
\alpha & \beta \\
\beta & \alpha
\end{array}
\right)
\end{align}
◯ 恒等置換(恒等写像ともいう)
集合の任意の元
を集合
の
へ対応させる写像も、集合
上の置換であるが、これを特に「集合
上の恒等置換」といい「
」で表す。
◯巡回置換
→略
◯偶置換と奇置換
・定理1:集合上の任意の置換
に対して、
と
の合成
も
上の置換となる。
・定理2:集合上の任意の置換
は、次の互換のうち、いくつかの重複を含めた合成によって表される。
\begin{align}
(1~~2), (2~~3), (3~~4), ..., (n-1~~n)
\end{align}
・定理3:集合上の任意の置換
は、いくつかの互換
の合成置換
として表され、「
が偶数であるか奇数であるか」は置換
に対して一意に定まる。
よって、定理3より、「偶置換」と「奇置換」を以下のように定義する。
ー偶置換:「
」とすると、
が偶数。
ー奇置換:「
」とすると、
が奇数。
2.2 置換群
個の元を持つ任意の有限集合
に対して、「置換」操作を行うとさまざまな集合が得られる。これらの集合は「n次置換群」「n次対称群」「n次交換群」に整理・分類することができる。
◯ n次対称群 の定義
個の元を持つ任意の有限集合
に対して、
上の置換全体からなる集合を「n次対称群」といい
で表す。
は次の性質を満たす。
(S1)の任意の元
に対して、
は
の元である
(S2)の任意の元
に対して、結合法則が成り立つ。
(S3)にある元
があって、
の任意の元
に対して、次の式を満たす。
(S4)の任意の元
に対して、次の式を満たす
の元
がある。
◯ n次交代群 の定義
個の元を持つ任意の有限集合
に対して、
上の偶置換全体からなる集合を「n次交代群」といい
で表す。n次交代群
はn次対称群
の部分集合であるから以下の性質を満たす。
(A1)の任意の元
に対して、
は
の元である
(A2)の任意の元
に対して、結合法則が成り立つ。
(A3)にある元
があって、
の任意の元
に対して、次の式を満たす。
(A4)の任意の元
に対して、次の式を満たす
の元
がある。
◯ n次置換群 の定義
一般に、n次対称群の部分集合を「n次置換群」といい
で表す。
(G1)の任意の元
に対して、
は
の元である
(G2)の任意の元
に対して、結合法則が成り立つ。
(G3)にある元
があって、
の任意の元
に対して、次の式を満たす。
(G4)の任意の元
に対して、次の式を満たす
の元
がある。
3. 群
3.1 群の定義
以下の性質(1)〜(3)を満たす集合を「演算子✳︎に対する群」という。
以下の性質(1)〜(4)を満たす集合を「演算子✳︎に対するアーベル群」という。
(1)演算✳︎に対して「結合法則」が成立。すなわち、集合の任意の元
に対して、
\begin{align}
(a~✳︎~b)~✳︎~c~=~a~✳︎~(b~✳︎~c)
\end{align}
(2)演算✳︎に対して「単位元」が存在する。すなわち、集合にある元
があって、集合
の任意の元
に対して、
\begin{align}
a~✳︎~e~=~e~✳︎~a~=~a
\end{align}
(3)演算✳︎に対して任意の元()の「逆元」(
)が存在する。すなわち、集合
の任意の元
に対して、
\begin{align}
a~✳︎~b~=~b~✳︎~a~=~e
\end{align}
(4)演算✳︎に対して「交換法則」が成立。すなわち、集合の任意の元
に対して、
\begin{align}
a~✳︎~b~=~b~✳︎~a
\end{align}
coming soon...
備忘・numpy.reshapeまとめ
よく忘れるのでメモしておく。
まず、テスト用の配列z(numpy.ndarray)を用意する。
zの形式は、3行4列。
import numpy as np z = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]]) ##-- IN --## z.shape ##-- OUT --## (3, 4)
1. 「reshape(1, -1)」
##-- IN --## z.reshape(1, -1) #or, np.reshape(z, (1, -1)) ##-- OUT --## array([[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]])
これは、以下の変形と同じ。
##-- IN --## z.reshape(1, 12) #or, np.reshape(z, (1, 12)) ##-- OUT --## array([[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]])
2. 「reshape(-1, 1)」
##-- IN --## z.reshape(-1, 1) #or, np.reshape(z, (-1, 1)) ##-- OUT --## array([[ 1], [ 2], [ 3], [ 4], [ 5], [ 6], [ 7], [ 8], [ 9], [10], [11], [12]])
これは、以下の変形と同じ。
##-- IN --## z.reshape(12, -1) #or, np.reshape(z, (12, -1)) ##-- OUT --## array([[ 1], [ 2], [ 3], [ 4], [ 5], [ 6], [ 7], [ 8], [ 9], [10], [11], [12]])
3. 「reshape(1, -1)」
##-- IN --## z.reshape(-1) #or, np.reshape(z, (-1)) ##-- OUT --## array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
scikit-learn : pythonで重回帰分析をやってみた

1. 重回帰分析についての所感
1.1. 用語など
- 英語だと, Multiple Regression.
- 変数の呼び方は色々ある.
{説明変数or予測変数or独立変数} vs {被説明変数or応答変数or目的変数} - いわゆる一般化線形モデル群(GLM)の一角.単回帰/重回帰/多項式回帰は線形モデル(LM)だが,ロジスティック回帰は狭義の線形モデル(LM)ではない.
- "線形(Linear)"という語は,「説明変数→目的変数」ではなく「説明変数の係数(パラメータ)→目的変数」という写像の性質を指している.
- 説明変数どうしの関係に対して,モデルは固定効果 or 変量効果を仮定する.両方の効果を仮定するものは「混合モデル」と呼ばれる.
- 誤差項が「正規分布に従う」と仮定するモデルは「一般線形モデル」,誤差が「任意の分布に従う」と仮定するモデルは,「一般化線形モデル」という.
1.2. モデル評価:「モデル」の性能を学習結果から評価する
- 決定係数R^2の他にも、MAE(平均絶対誤差), MSE(平均二乗誤差)など色々ある.だいたい似たような結果になる.詳細はこちら.
- 自由度調整済みR^2は, scikit-learnにないらしく,自分で定義する必要あり.
- 「帰無仮説 : 偏回帰係数が0」でn元配置分散分析(F検定)をするのが通説.scikit-learn だと簡単にできない(?).
- R^2・MAE・MSEの値や仮説検定の結果に加えて、残差分析(プロット)などの可視化による検証が有効.
1.3. モデル選択:「モデルの適用」に対する妥当性を検証する
- 「外れ値」はないか?→欠損処理
- 「系列相関」はないか?→ダービン・ワトソン検定
- 「データが独立同分布からなる」という仮定は妥当か?→残差分析、残差プロット
- 「誤差項が独立同分布からなる」という仮定は妥当か?→残差分析、残差プロット
- 「誤差項は正規分布に従う」という仮定は妥当か?→F検定や信頼区間を見直し
- 「説明変数が互いに独立」という仮定は妥当か?→交互作用、多重線形性の検証
- 「データに対する残差の等分散性」という仮定は妥当か?→重み付き2乗法
- 「変数選択」は妥当か?→自由度調整済みR^2、マローズのCp規準、AIC
- 「Overfit、予測能力、汎化能力」は妥当か?→AIC、WAIC、Cross validation
- 「尤もらしさ、データへの表現力」は妥当か?→BIC、Bayse factor
1.4. Pythonでの実装まわり
- 重回帰分析に関しては,pythonよりRの方が早い説.Rのglm()が超優秀.
- もちろん,scikit-learn以外のモジュールを使う方法もある.例:statsmodels
2. scikit-learnのサンプルデータセットで重回帰分析を試してみる
2.1. データ:skearn.datasets.load_boston
データセットはscikit-learnにあるサンプルデータ「ボストン市の地域情報」を使う.今回は,以下の9つの特徴量を使う.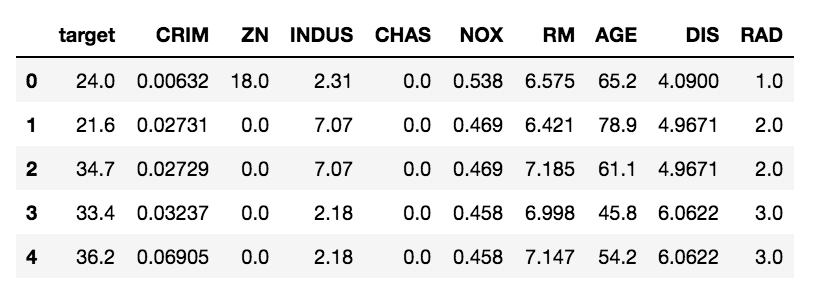
- target - 住宅価格
- CRIM - 犯罪発生率
- ZN - 住居区画の密集度
- INDUS - 非小売業の土地割合
- CHAS - チャールズ川 (1: 川の周辺, 0: それ以外)
- NOX - NOx濃度
- RM - 住居の平均部屋数
- AGE - 1940年より前に建てられた物件割合
- DIS - 5つのボストン市の雇用施設からの重み付き距離
- RAD - 大きな道路へのアクセスしやすさ
データの散布図行列*1はこんな感じ(↓).
相関がありそうな説明変数のペアについては, 多重共線性を考えるべき.

2.2. モデル:9次多項式でfitting
ボストン市の住宅価格targetを目的変数にして重回帰モデルを作る.今回のモデルは,9次元空間から1次元空間への写像を9元多項式で表現したもの.
※ 目的変数:target (1コ)
※ 説明変数:CRIM, ZN, INDUS, CHAS, NOX, RM, AGE, DIS, RAD (9コ)
※ 誤差項 :u (平均0, 正規分布に従う)
2.3. 前処理 : sklearn.model_selection.train_test_split
train-testの分割では一番簡単なホールド・アウト法を使う.データの正規化や次元削減は省略した.
3. プログラム - Python3.x系
import numpy as np import pandas as pd from sklearn.datasets import load_boston # make data samples boston = load_boston() data = pd.DataFrame(boston.data, columns = boston.feature_names) target = pd.DataFrame(boston.target, columns = ['target']) df = pd.concat([target, data], axis = 1) df = df.iloc[:, :10] # set x to explanatory variable # set y to response variable x = df.iloc[:, 1:] y = df.loc[:, ['target']] # split data by Hold-out-method from sklearn.model_selection import train_test_split x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.3, random_state = 0) # fitting train-data to the model from sklearn.linear_model import LinearRegression lr = LinearRegression() lr.fit(x_train, y_train) # predicting y of test-data by the model y_test_pred = lr.predict(x_test) # estimated value of params print('\n[Estimated values of the params]') print(' Intercept :', lr.intercept_) print(' Coefficient :', lr.coef_) # model evaluation from sklearn.metrics import mean_absolute_error, mean_squared_error print('\n[Model evaluation]') print(' R^2 on train : %.5f' % lr.score(x_train, y_train)) print(' R^2 on test : %.5f' % lr.score(x_test, y_test)) print(' MAE (Mean-Absolute-Error) :', mean_absolute_error(y_test, y_test_pred)) print(' MSE (Mean-Squared-Error) :', mean_squared_error(y_test, y_test_pred)) print(' RMSE (Rooted-MSE) :', np.sqrt(mean_squared_error(y_test, y_test_pred)))
以上を実行すると, 次のような結果を得られる. Oh, that's the overfitting! :D
[Estimated values of the params] Intercept : [-1.83284178] Coefficient : [ [-0.18424554 0.06424141 -0.22994428 4.17534912 -8.45210943 6.93761463 -0.06944658 -1.81172533 -0.07995724] ] [Model evaluation] R^2 on train : 0.66568 R^2 on test : 0.54068 MAE (Mean-Absolute-Error) : 4.133489445028324 MSE (Mean-Squared-Error) : 38.245841746617565 RMSE (Rooted-MSE) : 6.184322254428335
回帰問題でよく使う評価指標については,下記の記事にまとめたので,よければどうぞ.
yul.hatenablog.com
4. 参考文献

- 作者:
- 出版社/メーカー: 東京大学出版会
- 発売日: 1991/07/09
- メディア: 単行本

- 作者:佐和 隆光
- 出版社/メーカー: 朝倉書店
- 発売日: 1979/04/01
- メディア: 単行本

- 作者:Trevor Hastie,Robert Tibshirani,Jerome Friedman
- 出版社/メーカー: 共立出版
- 発売日: 2014/06/25
- メディア: 単行本

- 作者:Trevor Hastie,Robert Tibshirani,Jerome Friedman
- 出版社/メーカー: Springer
- 発売日: 2008/12/01
- メディア: ハードカバー
*1:関数seaborn.pairplot()を使う
メモ: CSに役立ちそうな数学
どんな分野であれ、最先端に進むためには数学に関するある程度の知識と教養が必要。
ということで 情報系をやる上で特に役立ちそうな分野をピックアップしてみます。
(パーフェクトに主観で語っているので、重大な思い違いがあるかもしれないです。)
Computer Scienceに役立ちそうな数学
→これを修めないと何も始まらない。
- 集合と位相
→集合は言わずもがなとして、位相も理解すれば思考の抽象度が上がりそう
→群と位相をきちんと理解できれば、色々役立ちそう
→最適化やアルゴリズム, データ構造, 計算量などを基礎づけているぽい
→高次元を定式化する時に必須. 線形代数を解析的に操作できる.
→数学の作法で統計学を扱うなら、空間(位相, 集合)の概念も理解する方が良い
→あらゆる工学で使われているし、電子/電気工学と相性がよい
- 数値解析(変分法, 差分法, 近似法)
→離散データの計測, 計算, 処理に不可欠.
→暗号や符号理論の基礎. 離散数学と相性良い?
- 数理論理学, 情報幾何, 計算代数幾何, 複雑性科学, 意味論
→情報とは何か?計算とは何か?を真剣に議論する際に.