AICの導出：平均対数尤度の摂動を近似する

このポストでは，赤池情報量規準(AIC, Akaike Information Criterion)について，特にその導出過程に留意しつつ解説します．AICは，線形モデル(+ガウスノイズ)のパラメータ選択問題を（必要条件の拘束が大きいものの）発展的に解いた偉大な研究成果であり，また，様々な学習問題において本質的な"汎化"問題を考える上でも非常に示唆的です．AICの導出過程を細かく記述した文献については，論文/書籍があるもののweb上には少ない印象を受けました．そこで，なるべく式展開を詳細しつつ，AICの有名な定義式（下式）が求められるまでの過程を記しておきたいと思います．

$$ \begin{equation} A I C = -2 \sum_{i=1}^{n} ~ \log f(x_i | \hat{\theta}_{MLE}( \boldsymbol{x}^n ) ) + 2 p \end{equation} $$

• サンプルサイズはとする．
• パラメータの次元はとする．
• 確率変数，そのサンプルの次元はとする．
• 確率変数，そのサンプルの次元はとする．

情報量規準 (シリーズ・予測と発見の科学)

赤池情報量規準AIC―モデリング・予測・知識発見

1. 確率モデルとKL情報量

未知の確率分布関数（=「真の分布」）に従って観測された個のデータサンプル を考えます．真の分布の近似として我々は確率モデルを を想定します．分布関数に対応する密度関数*1をそれぞれと定義します．

変数 の真の分布　 ：

変数 の確率モデル ：

このとき，モデルのよさは「真のモデルに対する確率分布としての近さ」によって評価できます．AIC(Akaike, 1973)では，分布間の近さを測る尺度として次のKL情報量(Kullback-Leibler, 1951)を採用しています．KL情報量は距離の公理のうち「対称性」以外をみたす疑距離であり，の値が小さいほどモデルはに近いと考えることができます．

$$ \begin{eqnarray} \mathbb{D}_{KL}(G ; F) & = & \mathbb{E}_{G} \left[ \log \frac{G(X)}{F(X)} \right] \\ & = & \int \log \frac{g(x)}{f(x)} ~ dG(x) \\ & = & \int_{- \infty}^{\infty} g(x) \log \frac{g(x)}{f(x)} ~ dx \end{eqnarray} $$

さらに，KL情報量を分解すると，「確率モデル に依存しない不確実性（変数 の平均情報量）」と「確率モデル に依存する不確実性（変数 のモデル による平均対数尤度）」に分けることができます．

$$ \begin{eqnarray} \mathbb{D}_{KL}(G ; F) & = & \int_{- \infty}^{\infty} g(x) \log \frac{g(x)}{f(x)} ~ dx \\ & = & \int_{- \infty}^{\infty} g(x) \log g(x) ~ dx - \int_{- \infty}^{\infty} g(x) \log f(x) ~ dx \\ & = & \mathbb{E}_{g} \left[ \log g(x) \right] - \mathbb{E}_{g} \left[ \log f(x) \right] \\ & = & - (X の平均情報量) - (X のモデル f による平均対数尤度) \end{eqnarray} $$

変数 の平均情報量 は，確率モデル の選び方に依らない量であり，データの背後にある現象（変数 の確率的構造）がもつ不確実性の下限です．すなわち，「モデルの，真のモデルに対する確率分布としての近さ」を評価する際には，変数 の平均対数尤度 にのみ注目すれば良いことがわかります．

平均対数尤度を最大化するモデル 　＝　KL情報量 を最小化するモデル

• なお，KL情報量の詳細については，下記記事で紹介しています． yul.hatenablog.com

2. パラメトリックモデルを考える

さて，多くの確率モデルでは，対象となる変数の他に，モデリングを拡張するための媒介変数として「パラメータ」を想定します． パラメータの値を陽に指定できる確率モデルを，一般に「パラメトリックモデル」と呼びます．ここからは，確率モデルと行った場合，パラメトリックモデルのことを指す事にします．

パラメータを中心に，問題を整理してみましょう．

ある変数 の確率構造 を捉えるために， 次元パラメータをもつパラメトリックモデル を想定します．推定に用いるデータサンプル を固定すると，モデルはの値によって決定されます．ここではパラメータを，最尤推定量 で置き換えることによって，確率モデル を構築します．以下に，よく使われる用語を整理しておきます．尤度(likelihood)とよばれる量は，すべてパラメータの関数として考えることができます．

• データサンプル に依存する量（データから計算可能）
  • （対数尤度）　　　
  • （最大対数尤度）　
    • ただし， （パラメータ の最尤推定量）
• データサンプル に依存しない量（データから計算不可能）
  • （平均対数尤度）　
  • （KL情報量）　　　

「モデル選択」の問題（あるいは「バイアス-バリアンス分解」「過学習」「汎化誤差」）とは，結局のところ，「具体的なデータから計算可能な量」から「データから計算不可能な量」を推定する際に生じる"偏り"(=バイアス)をどのようにコントロールするのか，を問うているのです．さらに，モデル選択の問題に，パラメトリックモデルかつ最尤推定という仮定をおけば，これはより具体的に，「対数尤度と平均対数尤度の"ズレ"(=バイアス)を評価して適切に割り引く」ことに他なりません．

平均対数尤度は，未知の関数で期待値をとっているためデータから計算不可能な量ですが，「サンプル数が大きい（）」場合，大数の法則を用いることで，対数尤度から推定することが可能です．AICでは，この関係式をヒントに，バイアスを補正した対数尤度（=平均対数尤度の推定量）を導出します．

$$ \frac{1}{n} \sum_{i=1}^{n} \log f(x_i | \theta) ~~ \underset{p}{\to} ~~ \mathbb{E}_{g(x)} \left[ \log f(X | \theta) \right] ~~~ (n \to \infty) $$

ここまでの流れをアルゴリズム風にまとめると以下のようになります． 特に注意すべきは，手続き(a)，(b)で現れる2つの量，対数尤度と平均対数尤度です．

3. バイアスの不偏推定量を求める

我々の目標/ゴールは，「 におけるモデル の平均対数尤度を計算すること」です．下図の白丸はデータから計算可能な（データに依存する）量を表しており， は平均対数尤度を最大化するパラメータです．ただし，データ から を見つけることはできません．AICでは，最尤推定量 を与えた際のモデル の対数尤度（=最大対数尤度）ではなく，最尤推定量 を与えた際のモデル の平均対数尤度によって，モデル選択を行います．ここで重要な量は，下図の で示された部分です．

モデル に対して，データサンプル を固定して， における「対数尤度と平均対数尤度の差 」を考えます．

$$ \begin{eqnarray} D & := & \left( データサンプル \boldsymbol{x}^n の対数尤度 \right) - \left( n \cdot 変数X の平均対数尤度 \right) \\ & = & \log f(\boldsymbol{x}^n | \hat{\theta}_{MLE}(\boldsymbol{x}^n)) - n \cdot \mathbb{E}_{g} \left[ \log f(X | \hat{\theta}_{MLE}(\boldsymbol{x}^n)) \right] \end{eqnarray} $$

さらに， はデータサンプル に依存するため，その期待値を考えます． データサンプル は密度関数 にしたがってばらつくことに注意すると，

$$ \begin{eqnarray} b(G) & := & \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ D \right] \\ & = & \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \log f(\boldsymbol{x}^n | \hat{\theta}_{MLE}(\boldsymbol{x}^n)) - n \cdot \mathbb{E}_{g} \left[ \log f(X | \hat{\theta}_{MLE}(\boldsymbol{x}^n)) \right] \right] \\ \end{eqnarray} $$

が定義されます． はバイアスと呼ばれる量です． に無理やり意味付けを与えると，「確率モデル に対する，データサンプル の最大対数尤度 の"ばらつき"の期待値」といえます．ここで，以下の関係が成り立つ事に注意してください．

$$ \begin{eqnarray} (最大対数尤度の期待値) + (バイアス) & = & n \cdot (\hat{\theta}_{MLE}における平均対数尤度) \\ \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \log f(\boldsymbol{x}^n | \hat{\theta}_{MLE}) \right] + b(G) & = & n \cdot \mathbb{E}_{g(x)} \left[ \log f(X | \hat{\theta}_{MLE}) \right] \\ \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \log f(\boldsymbol{x}^n | \hat{\theta}_{MLE}) + D \right] & = & n \cdot \mathbb{E}_{g(x)} \left[ \log f(X | \hat{\theta}_{MLE}) \right] \end{eqnarray} $$

3.1 Dを分解する．

における「対数尤度と平均対数尤度の差 」は， を用いて次のように分解できます．

$$ \begin{eqnarray} D & = & \log f(\boldsymbol{x}^n | \hat{\theta}_{MLE}) - n \cdot \mathbb{E}_{g} \left[ \log f(X | \hat{\theta}_{MLE}) \right] \\ & = & \log f(\boldsymbol{x}^n | \hat{\theta}_{MLE}) - \log f(\boldsymbol{x}^n | \theta_0) \\ & ~ & + \log f(\boldsymbol{x}^n | \theta_0) - n \cdot \mathbb{E}_{g(x)} \left[ \log f(X | \theta_0) \right] \\ & ~ & + n \cdot \mathbb{E}_{g(x)} \left[ \log f(X | \theta_0) \right] - n \cdot \mathbb{E}_{g(x)} \left[ \log f(X | \hat{\theta}_{MLE}) \right] \\ \end{eqnarray} $$

よって，以下のように を定義すると， が成り立ちます．

$$ \begin{eqnarray} D_1 & = & \log f(\boldsymbol{x}^n | \hat{\theta}_{MLE}) - \log f(\boldsymbol{x}^n | \theta_0) \\ D_2 & = & \log f(\boldsymbol{x}^n | \theta_0) - n \cdot \mathbb{E}_{g(x)} \left[ \log f(X | \theta_0) \right] \\ D_3 & = & n \cdot \mathbb{E}_{g(x)} \left[ \log f(X | \theta_0) \right] - n \cdot \mathbb{E}_{g(x)} \left[ \log f(X | \hat{\theta}_{MLE}) \right] \\ \end{eqnarray} $$

（１） の期待値を計算する

の関数：対数尤度 を，最尤推定量 [\hat{\theta}_{MLE}] のまわりでTaylor展開すると，

$$ \ell(\theta) \simeq \ell(\hat{\theta}_{MLE}) + { (\theta - \hat{\theta}_{MLE}) }^{\mathrm{T}} \frac{\partial \ell(\theta)}{\partial \theta} {\mid}_{\theta = \hat{\theta}_{MLE}} + \frac{1}{2} { (\theta - \hat{\theta}_{MLE}) }^{\mathrm{T}} \frac{{ \partial}^2 \ell(\theta) }{\partial \theta \partial \theta^\mathrm{T}} {\mid}_{\theta = \hat{\theta}_{MLE}} (\theta - \hat{\theta}_{MLE}) $$

さらに， を代入すると，

$$ \ell(\theta_0) \simeq \ell(\hat{\theta}_{MLE}) + { (\theta_0 - \hat{\theta}_{MLE}) }^{\mathrm{T}} \frac{\partial \ell(\theta)}{\partial \theta} {\mid}_{\theta = \hat{\theta}_{MLE}} + \frac{1}{2} { (\theta_0 - \hat{\theta}_{MLE}) }^{\mathrm{T}} \frac{{ \partial}^2 \ell(\theta) }{\partial \theta \partial \theta^\mathrm{T}} {\mid}_{\theta = \hat{\theta}_{MLE}} (\theta_0 - \hat{\theta}_{MLE}) $$

ここで，

$$ \begin{eqnarray} \frac{\partial \ell(\theta)}{\partial \theta} {\mid}_{\theta = \hat{\theta}_{MLE}} & = & {\bf 0} \\ \\ \frac{1}{n} \frac{{ \partial}^2 \ell(\theta) }{\partial \theta \partial \theta^\mathrm{T}} {\mid}_{\theta = \hat{\theta}_{MLE}}
& = & \frac{1}{n} \frac{{ \partial}^2 \sum_{i=1}^{n} \log f(x_i | \theta) }{\partial \theta \partial \theta^\mathrm{T}} {\mid}_{\theta = \hat{\theta}_{MLE}} \\ & \underset{p}{\to} & \mathbb{E}_{g(x)} \left[ \frac{ {\partial}^2 \log f(X|\theta)}{\partial \theta \partial \theta^\mathrm{T}} {\mid}_{\theta = \theta_0} \right] = J(\theta_0) ~~~~~~ (n \to \infty) \end{eqnarray} $$

が成り立つから，

$$ \ell(\theta_0) \approx \ell(\hat{\theta}_{MLE}) + \frac{n}{2} { (\theta_0 - \hat{\theta}_{MLE}) }^{\mathrm{T}} J(\theta_0) (\theta_0 - \hat{\theta}_{MLE}) $$

が得られます．よって，

$$ \begin{eqnarray} \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ D_1 \right]
& = & \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \log f(\boldsymbol{x}^n | \hat{\theta}_{MLE}) - \log f(\boldsymbol{x}^n | \theta_0) \right] \\ & = & \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \ell( \hat{\theta}_{MLE} ) - \ell( \theta_0 ) \right] \\ & \approx & \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \frac{n}{2} { (\theta_0 - \hat{\theta}_{MLE}) }^{\mathrm{T}} J(\theta_0) (\theta_0 - \hat{\theta}_{MLE}) \right] \\ & = & \frac{n}{2} \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \mathrm{tr} \left\{ J(\theta_0) (\theta_0 - \hat{\theta}_{MLE}) { (\theta_0 - \hat{\theta}_{MLE}) }^{\mathrm{T}} \right\} \right] \\ & = & \frac{n}{2} \mathrm{tr} \left\{ J(\theta_0) ~ \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ (\theta_0 - \hat{\theta}_{MLE}) { (\theta_0 - \hat{\theta}_{MLE}) }^{\mathrm{T}} \right\} \right] \\ & = & \frac{n}{2} \mathrm{tr} \left\{ J(\theta_0) ~ \frac{1}{n} {J(\theta_0)}^{-1} I(\theta_0) {J(\theta_0)}^{-1} \right\} \\ & = & \frac{1}{2} \mathrm{tr} \left\{ I(\theta_0) {J(\theta_0)}^{-1} \right\} \end{eqnarray} $$

（２） の期待値を計算する

$$ \begin{eqnarray} \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ D_2 \right] & = & \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \log f(\boldsymbol{x}^n | \theta_0) - n \cdot \mathbb{E}_{g(x)} \left[ \log f(X | \theta_0) \right] \right] \\ & = & \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \log f(\boldsymbol{x}^n | \theta_0) \right] - n \cdot \mathbb{E}_{g(x)} \left[ \log f(X | \theta_0) \right] \\ & = & n \cdot \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \frac{1}{n} \sum_{i=1}^{n} \log f(x_i | \theta_0) \right] - n \cdot \mathbb{E}_{g(x)} \left[ \log f(X | \theta_0) \right] \\ & = & n \cdot 0 = 0 \end{eqnarray} $$

（３） の期待値を計算する

$$ \begin{eqnarray} \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ D_3 \right] & = & \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ n \cdot \mathbb{E}_{g(x)} \left[ \log f(X | \theta_0) \right] - n \cdot \mathbb{E}_{g(x)} \left[ \log f(X | \hat{\theta}_{MLE}) \right] \right] \\ & = & n \cdot \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \mathbb{E}_{g(x)} \left[ \log f(X | \theta_0) - \log f(X | \hat{\theta}_{MLE}) \right] \right] \\ \end{eqnarray} $$

の関数：を， のまわりでTaylor展開すると，

さらに， の任意性から を代入すると，

となります．ここで「確率モデル によって，真の分布 が表現可能である」という仮定をおきます．

$$ \exists \theta_0 \in \Theta, ~ \forall x \in \mathbb{R}^d, ~~~ f(x|\theta_0) = g(x) $$

よって， の関数：に， を代入すると，

$$ \mathbb{E}_{g(x)} \left[ \frac{\partial \log f(X|\theta)}{\partial \theta} \mid_{\theta_0} \right] = \mathbb{E}_{g(x)} \left[ \frac{\partial \log g(X)}{\partial \theta} \right] = \int g(x) \frac{\partial \log g(x)}{\partial \theta} ~ dx = \boldsymbol{0} $$

が成り立つので，Taylor展開の第1項は消えて，

$$ \mathbb{E}_{g(x)} \left[ \log f(X | \hat{\theta}_{MLE}) \right] \approx \mathbb{E}_{g(x)} \left[ \log f(X | \theta_0 ) \right] - \frac{1}{2} {(\hat{\theta}_{MLE} - \theta_0)}^{\mathrm{T}} J(\theta_0) (\hat{\theta}_{MLE} - \theta_0) $$

が成り立ちます．

$$ \begin{eqnarray} \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ D_3 \right] & = & \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ n \cdot \mathbb{E}_{g(x)} \left[ \log f(X | \theta_0) \right] - n \cdot \mathbb{E}_{g(x)} \left[ \log f(X | \hat{\theta}_{MLE}) \right] \right] \\ & = & n \cdot \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \mathbb{E}_{g(x)} \left[ \log f(X | \theta_0) \right] - \mathbb{E}_{g(x)} \left[ \log f(X | \hat{\theta}_{MLE}) \right] \right] \\ & \approx & n \cdot \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \frac{1}{2} {(\hat{\theta}_{MLE} - \theta_0)}^{\mathrm{T}} J(\theta_0) (\hat{\theta}_{MLE} - \theta_0) \right] \\ & = & \frac{n}{2} \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ {(\hat{\theta}_{MLE} - \theta_0)}^{\mathrm{T}} J(\theta_0) (\hat{\theta}_{MLE} - \theta_0) \right] \\ & = & \frac{n}{2} \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \mathrm{tr} \left\{ J(\theta_0) (\hat{\theta}_{MLE} - \theta_0) {(\hat{\theta}_{MLE} - \theta_0)}^{\mathrm{T}} \right\} \right] \\ & = & \frac{n}{2} \mathrm{tr} \left\{ J(\theta_0) ~ \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ (\hat{\theta}_{MLE} - \theta_0) {(\hat{\theta}_{MLE} - \theta_0)}^{\mathrm{T}} \right] \right\} \\ & = & \frac{n}{2} \mathrm{tr} \left\{ J(\theta_0) ~ \frac{1}{n} {J(\theta_0)}^{-1} I(\theta_0) {J(\theta_0)}^{-1} \right\} \\ & = & \frac{1}{2} \mathrm{tr} \left\{ I(\theta_0) {J(\theta_0)}^{-1} \right\} \end{eqnarray} $$

3.2 バイアスの推定量（Dの漸近推定量）

に関する計算結果をまとめると，バイアス は結局次のように近似されます．

$$ \begin{eqnarray} b(G) &= & \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ D \right] \\ &= & \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ D_1 + D_2 + D_3 \right] \\ &= & \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ D_1 \right] + \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ D_2 \right] + \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ D_3 \right] \\ &= & \frac{1}{2} \mathrm{tf} \left\{ I(\theta_0) {J(\theta_0)}^{\mathrm{-1}} \right\} + 0 + \frac{1}{2} \mathrm{tf} \left\{ I(\theta_0) {J(\theta_0)}^{\mathrm{-1}} \right\} \\ &= & \mathrm{tr} \left\{ I(\theta_0) {J(\theta_0)}^{\mathrm{-1}} \right\} \end{eqnarray} $$

3.3 2つの重要な行列

パラメータ を任意の値に固定したとき，確率モデル のFisher情報量行列 と，平均対数尤度関数 のHesse行列 が定義されます． ここで， における は次のように記述されます．

• 確率モデル のFisher情報量行列

$$ \begin{eqnarray} I(\theta_0) & := & \ \mathbb{E}_{g(x)} \left[ \left( \frac{\partial \log f(X | \theta)}{\partial \theta} \right) \left( \frac{\partial \log f(X | \theta)}{\partial {\theta}^{\mathrm{T}}} \right) \mid_{\theta_0} \right] \\ I(\theta_0)_{ij} & := & - \mathbb{E}_{g(x)} \left[ \left( \frac{\partial \log f(X | \theta)}{\partial \theta_i} \right) \left( \frac{\partial \log f(X | \theta)}{\partial \theta_j} \right) \mid_{\theta_0} \right], ~~~ \forall i, j \in [1, p] \end{eqnarray} $$

• 平均対数尤度関数 のHesse行列

$$ \begin{eqnarray} J(\theta_0) & := & - \mathbb{E}_{g(x)} \left[ \frac{ {\partial}^{2} \log f( X | \theta) }{\partial \theta \partial {\theta}^{\mathrm{T}}} \mid_{\theta_0} \right] \\ J(\theta_0)_{ij} & := & - \mathbb{E}_{g(x)} \left[ \frac{ {\partial}^{2} \log f( X | \theta) }{\partial \theta_i \partial \theta_j} \mid_{\theta_0} \right], ~~~ \forall i, j \in [1, p] \end{eqnarray} $$

行列， では「微分演算」と「内積演算」の順序が異なることに注意してください．さらに， に対して，

$$ \forall x, ~ f(x|\theta_0) = g(x) ~~~ \Longrightarrow ~~~ I(\theta_0) = J(\theta_0) $$

が成り立ちます．

4.AICの導出

さて，バイアスの不偏推定量が求められたので，これによってAICを導出しましょう．

目標
データサンプルから求めたパラメータ の最尤推定量 を使って求めた確率モデル に対して，その対数尤度 （=最大対数尤度）ではなく，平均対数尤度 の値によって，評価を与える．

ここで，

$$ \exists \theta_0 \in \Theta \subset \mathbb{R}^p, \forall x, ~~~ f(x|\theta_0) = g(x) ~~~ \cdots ~~~ (仮定*) $$

という仮定をおくと，バイアス は 行列 を用いて

$$ b(G) = \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ D \right] \simeq \mathrm{tr} \left\{ I(\theta_0) {J(\theta_0)}^{\mathrm{-1}} \right\} $$

と近似できます．さらに，仮定 より行列 が成り立つから，

$$ \mathrm{tr} \left\{ I(\theta_0) {J(\theta_0)}^{\mathrm{-1}} \right\} = \mathrm{tr} \left\{ I(\theta_0) {I(\theta_0)}^{\mathrm{-1}} \right\} = \mathrm{tr} \left\{ I_p \right\} = p \\ i.e. ~~~ b(G) \simeq p $$

を得ます．よって，対数尤度からバイアス を補正することにより，平均対数尤度の推定量(=AIC)を求めることができます．

$$ \begin{eqnarray} (最大対数尤度の期待値) + (バイアス) & = & n \cdot (\hat{\theta}_{MLE}における平均対数尤度) \\ \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \log f(\boldsymbol{x}^n | \hat{\theta}_{MLE}) \right] + b(G) & = & n \cdot \mathbb{E}_{g(x)} \left[ \log f(X | \hat{\theta}_{MLE}) \right] \\ \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \log f(\boldsymbol{x}^n | \hat{\theta}_{MLE}) + p \right] & \simeq & \mathbb{E}_{g(x)} \left[ n \cdot \log f(X | \hat{\theta}_{MLE}) \right] \\ \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \sum_{i=1}^{n} \log f(x_i | \hat{\theta}_{MLE}) + p \right] & \simeq & \mathbb{E}_{g(x)} \left[ n \cdot \log f(X | \hat{\theta}_{MLE}) \right] \end{eqnarray} $$

上式の左辺を2倍すれば，AICの定義式が求められます．

$$ \begin{equation} A I C = -2 \sum_{i=1}^{n} \log f(x_i | \hat{\theta}_{MLE}) + 2 p \end{equation} $$

*1:離散変数の場合は密度関数は定義できません．簡単のためここでは連続変数のみを考えます．

PAC学習と計算論的学習理論(Computatinonal Learning Theory)の文献まとめ

　PAC学習 (Probability Approximately Correct learning) とは、イギリスの理論計算機科学者 Leslie Valiant が1984年に以下の論文で初めて提唱した概念で、計算機科学の分野でそれまで研究されていた一般的な計算アルゴリズムの効率性・複雑性に対して、学習アルゴリズムに関しても同様の議論を行うために定義されたものです。

"A theory of the learnable"
Valiant, L. G. (1984). Communications of the ACM 1984 pp1134-1142.

　Valiant は、統計学の分野である「パターン認識(Pattern recognition)」や「決定理論(Decision theory)」の諸問題を、理論計算機科学の分野である計算複雑性理論(Computational Complexity Theory, CCT)と結びつけることで、学習アルゴリズムの持つ「複雑性」を定義しています。具体的に言うと、計算複雑性理論における「多項式時間で計算可能な解法が存在する問題(クラスP)」の定義と近しい形で、「実現可能な学習アルゴリズム」のクラスを定義しました。やがて、Valiantにより創始された学習アルゴリズムに関する一連の研究分野は計算論的学習理論(Computational Learning Theory, CLT)と呼ばれるようになり、今日に至ります。PAC学習の研究成果としては、例えば機械学習モデルの持つ汎化性能についての上界を与えるものなどがあり、近年ではソフトマージンSVMやDeep Learningの汎化誤差に関して、計算論的学習理論の研究者から、たくさんの関連論文が出ています。

　2019年2月現在、機械学習の隆盛下においても、計算論的学習理論やPAC学習に関する日本語の解説はあまりありませんが、「PAC learning」でGoogle検索すると、Introduction, Tutorioal, Surveyといった名前のつく英語の解説文献がそこそこ見つかります。個人的には、以下の文献がわかりやすかったです。

"Overview of the Probably Approximately Correct (PAC) Learning Framework" (David Haussler, UC Santa Cruz, July 2010)

"PAC Learnability" (Karl Stratos, TTIC, September 2016)

　このポストでは、Valiantが導入した計算論的学習理論における重要な2つの概念"true error(generalization error)", "PAC learnability"の定義を紹介し、参考論文を備忘として留めておきます。

定義1（true error or generalization error）
　学習したい"概念"クラス とそれに対応づけられた確率変数の集合 に対して、学習アルゴリズム を考える。ただし、 に対して定義される確率分布を とおく。確率分布 に対して独立同分布となる コのサンプル と、それに対応する"概念" のペアからなる訓練集合 によって学習を行い仮説 を立てる。このとき、仮説 の真の誤差(true error)あるいは汎化誤差(generalization error)を次式で定義する。

$$ error(h) := \underset{x ~ \sim~ \mathcal{D}}{Pr} \bigl( h_{S}(x) \neq c(x) \bigr) $$

定義2（PAC learnable）
　"概念"クラス がPAC学習可能であるとは、以下の条件を満たす学習アルゴリズム が存在し、かつ学習に必要な訓練集合の大きさ の下限に対して という関係を満たす多項式 が存在することである。

$$ \forall \varepsilon, \delta \in [0, 1], ~~ \forall m \in \mathbb{N}, ~~ \forall c \in C, ~~ \forall \mathcal{D} ~on~ \mathcal{X}, \\ \underset{S ~ \sim~ \mathcal{D}^{m} \times C^{m}}{Pr} \Bigl( \underset{x ~ \sim~ \mathcal{D}}{Pr} \bigl( h_{S}(x) \neq c \bigr) \leq \varepsilon \Bigr) \geq 1 - \delta $$

※ PAC学習では、ある訓練集合 に対して、高い確率で「高い予測精度のモデル」を作ることができる学習アルゴリズム を考える。"PAC Learnable"の定義は抽象的だが、確率分布によって定まる汎化誤差(true error)を念頭においており、PAC学習の分野の成果は、実際に使われている多くの確率モデル・学習アルゴリズムに対する誤差理論へ適用できる。

※ ある訓練集合 に対して仮説と学習アルゴリズムの関係は で与えられることに注意。

• 訓練集合 ：学習アルゴリズムを構成するためのデータ
• 仮説 ：学習アルゴリズム の出力結果
• 概念 ：学習アルゴリズム で出力されるもの
• 仮説集合 ：仮説 の集合
• 概念集合 ：概念 の集合

　ところで、「学習アルゴリズム 」という表現は、計算機科学・計算理論の色が根強く反映されていると思います。すなわち、数理統計学(確率＆解析学)のお気持ちとしては、学習は、「確率変数の集合間の写像(関数)を、有限集合から近似する計算操作」として解釈されますが、ここでは近似すべき関数の方が強調されているように感じます。

• 関数近似に要する計算/アルゴリズムに主眼をおく。（計算機科学・計算理論）
• 計算/アルゴリズムによって近似する関数に主眼をおく。（数理統計学）

アラン・チューリングは「計算する」とは何か？を定義し「計算できること/できないこと」に厳密な線引きを与えましたが、当然「学習する」とは何か？にも定義が必要です。計算論的学習理論では、計算の枠組みを拡張することによって、学習を同様のスコープで捉えているように思います。

論文リスト

PAC Learningおよび計算論的理論に関する論文

• "On the Computational Complexity of Approximating Distributions by Probabilistic Automata" (Naoki Abe et al. 1992)

• "Learnability and the Vapnik-Chervonenkis Dimension" (Anselm Blumer et al. 1989)

• "Decision Theoretic Generalizations of the PAC Model for Neural Net and Other Learning Applications" (David Haussler 1989)

• "Efficient Distribution-Free Learning of Probabilistic Concepts" (Michael J. Kearns 1989)

• "Computational learning theory: survey and selected bibliography" ( Dana Angluin 1992)

PAC-Baysian Theory*1に関する論文

• "Some PAC-Bayesian Theorems" (David A. McAllester 1999)

• "Simplified PAC-Bayesian Margin Bounds"（David A. McAllester, 2003）

参考サイト

以下の記事は、PACを含む計算論的学習理論を概説しており、勉強になります。

qiita.com

*1:PAC LearningとBayse推定を組み合わせた理論

最尤推定量とワルド検定・スコア検定・尤度比検定

1. パラメータの尤もらしさに関する統計的仮説検定

　何らかのパラメトリックな確率モデル とコのデータサンプル（標本） に対して定義される対数尤度関数 を用いて、「あるパラメータ が最尤推定量 と一致しているかどうか」に真偽を与える統計的仮説検定を考えます。すなわち、仮説：

・帰無仮説
・対立仮説

を設けて、帰無仮説 を有意水準 で棄却する条件を、データ（標本）に基づく統計量とその分布から求めます。

　このポストでは、上記の検定方式として、Wald検定・Score検定・尤度比検定の3つを紹介します。これらは、パラメータ空間 から への写像である対数尤度関数 を中心に考えると、自然な導出であることがわかります。（下図参照）

1.1 ワルド検定（Wald test）

ワルド検定では、現在のパラメータ と最尤推定量 との差を基に検定を行います。

最尤推定量 に対するワルド検定（Wald test）

最尤推定量の漸近正規性（Asymptotic normality）：

が成り立つとき、仮説：

・帰無仮説
・対立仮説

における帰無仮説 の有意水準 の棄却域 は、

で与えられる。

1.2 スコア検定（Score test）

スコア検定では、現在のパラメータ の対数尤度関数における傾き（スコア関数）を基に検定を行います。

最尤推定量 に対するスコア検定（Score test）

スコア関数 とフィッシャー情報量 の定義

より、スコア関数 の平均と分散が

であることから、中心極限定理（CLT, Central Limit Theorem）を用いて、

が成り立つ。よって、仮説：

・帰無仮説
・対立仮説

における帰無仮説 の有意水準 の棄却域 は、

で与えられる。

1.3 尤度比検定（Likelihood ratio test）

尤度比検定では、現在のパラメータ の対数尤度と最尤推定量 との対数尤度の差を基に検定を行います。

最尤推定量 に対する尤度比検定（Likelihood ratio test）

尤度比検定統計量 を

と定義すると、仮説：

・帰無仮説
・対立仮説

において、帰無仮説 の下で、

が成り立つことから、帰無仮説 の有意水準 の棄却域 は、

で与えられる。

2. KL-divergenceとFischer情報量の関係

2.1 スコア関数とFischer情報量の定義

　スコア関数 を以下のように定義します．

対数関数の微分に注意すると，スコア関数 の期待値は0になります．

さらに，スコア関数の分散は，Fischer情報量 といい，以下のように計算されます．

パラメータ がn次元の場合，スコア関数は を用いて定義されるn次元ベクトル，Fischer情報量 は 行列となります．

2.2 KL-divergence

ここで、パラメータ の尤度 と、パラメータ の値を微小量 だけ変化させたときの尤度 との乖離度として、KL-divergenceを考えます。

さらに、 を の関数とみて、 のまわりでテイラー展開（マクローリン展開）をすると、

となります。よって、パラメータ の微小変化に対する KL-divergence：

の局所二次近似は、

となります。すなわち、パラメータ のFischer情報量は、パラメータ の微小変化に対する KL-divergenceと密接に関連した量であることがわかります。以上の結果は、次の定理にまとめられます。

の対数尤度関数 に基づいて導かれる検定および統計量をまとめると下図のようになります。

　最尤推定は、さまざまな確率モデルに対する最適化（学習）の基本であり、尤度関数（損失関数）の挙動を正確に把握することがとても重要です。Deep learningなど、高次元のパラメータ空間をもつ確率モデルの場合でも、二次の偏導関数（ヘッセ行列）によって、尤度関数の凸性・曲率が全て記述*1され、これはパラメータに対するFischer情報量行列と密に関連します。すなわち、Fischer情報量行列が正則行列でない*2場合、尤度関数はパラメータに対して非凸で複雑な関数となり、最尤推定量を探索することはより難しくなります。

Fischer情報量行列の定義やhessianとの関連については，以下のブログ記事が参考になります．

wiseodd.github.io

3. 参考書籍

新装改訂版 現代数理統計学

現代数理統計学の基礎 (共立講座 数学の魅力)

Statistics

*1:線形空間では基底ベクトルに対する微分さえわかれば、あらゆる方向に対する勾配がその線形結合として表現可能です。

*2:すべての固有値が正である行列のことを、正則行列といいます。これに対し，正則行列ではない行列を特異行列ということがあります。

ガウス過程と回帰モデル（線形~線形基底~ガウス過程）

※ このポストの内容は、PRML下巻6章とGPML2章を参考にしています。

www.microsoft.com www.gaussianprocess.org

1. ガウス過程（GP, Gaussian Process）

1.1 ガウス分布の共役性

　任意の確率モデル に対して の事前分布 としてガウス分布を仮定した場合、ベイズの定理によって求められる の事後分布 もガウス分布に従います。つまり、ガウス分布に従うパラメータ について、任意の確率モデル とデータサンプル から、事後分布 を求める操作はガウス分布の中で閉じています。一般に、「事前分布としてある確率分布を仮定すると、事後分布も同じ確率分布に従う」という性質を共役性といい、ガウス分布は共役性をもちます。

$$ \begin{eqnarray} (Posterior~of~w) & = & \frac{(likelihood ~of~ X^{n})\times(Prior~of~w)}{(Evidence~of~the~model)} \\ \\ p(w|X^{n}) & = & \frac{p(X^{n}|w)p(w)}{\int p(X^{n}|w)p(w) ~dw} \end{eqnarray} $$ $$ p(w) \sim N(\mu, s) ~ \Rightarrow ~ p(w|X^{n}) \sim N(\mu', s') $$

1.2 ガウス分布の切断と周辺化

　それぞれがガウス分布に従う「互いに独立でない」確率変数列 を考えます。このとき、確率変数列 はNコの確率変数 のペアであるため、確率変数列 そのものを 次元の確率変数として扱うことができます。同様に、確率変数列 における「任意の コの部分列」は 次元の確率変数として扱えます。

　平均が で、共分散行列が のN次元ガウス分布に従う確率変数 ：

に対して、（）による分割を考えます。

このとき、 は以下のようなガウス分布に従います。

さらに、「 の共分散行列 は半正定値対称行列である」ことから、次式が成り立ちます。

ここで、「 は独立ではない」ことに注意すると、条件つき確率 は次のように与えられ、条件つき平均 と条件つき共分散行列 からなるガウス分布に従うことがわかります。

を手元にあるデータサンプル、 を新しいデータサンプルと捉えると、これらを結合した に対してガウス過程を導入することができます。

1.3 ガウス過程の定義

　任意の組が同時ガウス分布（joint Gaussian distribution）に従うような確率変数の集合 を，ガウス過程（Gaussian Process, GP）と定義します。ガウス分布とガウス過程を比較すると以下のようになります。

• ガウス分布（Gaussian distribution）
  • 任意のガウス分布 は、平均 と共分散行列 によって完全に記述される。

• ガウス過程（Gaussian Process, GP）
  • 任意のガウス過程 は、平均関数 と共分散関数 によって完全に記述される。

2. さまざまな回帰モデルの比較

2.1 回帰問題とは？

　まず、回帰（Regression）に一般的な定義を与えてみます。

　確率変数 の実現値からなるNコのデータサンプル：

$$ \mathcal{D} := \left\{ \left( \begin{array}{c} {\bf x}_1 \\ y_1 \end{array} \right), \dots, \left( \begin{array}{c} {\bf x}_N \\ y_N \end{array} \right) \right\} $$

を用いて、 の値から の値を推定（予測）するモデル：

$$ f: X \in \mathbb{R}^{d} \to Y \in \mathbb{R} $$

を作りたい。

ここで、モデル による推定値 と真値 との推定誤差 を次のように定義し、

$$ \varepsilon_i := y_i - f({\bf x}_i) ~~~ (i=1, \dots, N) $$

さらに、各 はそれぞれ独立に同じパラメータをもつガウス分布に従うと仮定すると、

$$ y_i = f({\bf x}_i) + {\varepsilon}_i ~~~ (i=1, \dots N) \\ {\varepsilon}_i \sim N \left( 0, \frac{1}{\beta} \right) $$

という等式が得られます。これをまとめると、

$$ p( y_i | {\bf x}_i, f) = N \left( f({\bf x}_i), \frac{1}{\beta} \right) $$

となり、回帰問題の目的を、「を定めることで，任意のに対する条件付き確率 を定めること」とベイズ的に解釈することも可能です。すなわち、次式（ベイズの定理）で、 はデータサンプル への「当てはまりの良さ（=尤度）」を表しますが、同時に、 によって、データサンプル から の事後確率と予測分布が決定されます。

$$ p( f | y_i, {\bf x}_i ) = \frac{ p( y_i | {\bf x}_i, f ) p(f) } {p( y_i | {\bf x}_i )} $$

　一般化に、回帰問題では、データサンプル とモデル に対して

$$ p( f | {\bf y}, {\bf X} ) = \frac{ p( {\bf y} | {\bf X}, f ) p(f) } {p( {\bf y} | {\bf X} )}, ~~ i.e. ~~ p( f | \mathcal{D} ) = \frac{ p( \mathcal{D} | f ) p(f) } {p( \mathcal{D} )} $$

という構造が現れます。次章以降で、具体的な回帰モデルについて、解説したいと思います。

2.2 線形回帰モデル

2.2.1 線形回帰モデルの準備

　もっとも　素朴な回帰モデルとして「線形回帰モデル」を考えます。モデルパラメータとして、重みベクトル を想定します。

$$ y_i = f({\bf x}_i) + \varepsilon_i, \\ f({\bf x}_i) = {\bf x}_i^{\rm T} {\bf w} = \left( \begin{array}{c} x_{i1}, \dots, x_{id} \end{array} \right) \cdot \left( \begin{array}{c} w_{1} \\ \vdots \\ w_{d} \end{array} \right), ~~~ \varepsilon_i \sim N \left( 0, \frac{1}{\beta} \right) $$

これらの関係式をまとめると、各 に対する の推定値は、次式のように「ばらつきを持った確率モデル」として表現されます。

$$ p( y_i | x_i, {\bf w} ) = N \left( y_i | f({\bf x}_i), \frac{1}{\beta}{\bf I} \right) = N \left( {\bf x}_i^{\rm T} {\bf w}, \frac{1}{\beta} \right) $$

さらに、個々データではなくデータセット 全体に対して、回帰モデル はどのように作用するのかをまとめて考えます。計画行列（design matrix） と、ベクトル を以下のように定義します。

$$ {\bf X} := \left( {\bf x}_1, {\bf x}_2, \dots, {\bf x}_N \right)= \left( \begin{array}{cccc} x_{11} & x_{21} & \dots & x_{N1}\\ x_{12} & x_{22} & \dots & x_{N2}\\ \vdots & \vdots & \dots & \vdots \\ x_{1N} & x_{2N} & \dots & x_{NN} \end{array} \right), ~~~ {\bf y} := \left( \begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_N \end{array} \right), ~~~ {\boldsymbol \varepsilon} := \left( \begin{array}{c} \varepsilon_1 \\ \varepsilon_2 \\ \vdots \\ \varepsilon_N \end{array} \right) $$

すると、「線形回帰モデル」は以下のように記述され、

$$ {\bf y} = f({\bf X}) + {\boldsymbol \varepsilon}, \\ f({\bf X}) = {\bf X}^{\rm T}{\bf w}, ~~~ \boldsymbol \varepsilon \sim N \left( {\bf 0}, \frac{1}{\beta}{\bf I}\right) $$

これらの関係式をまとめると、 データセット における の推定値は、次式のように「ばらつきを持った確率モデル」として表現されます。

$$ p( {\bf y} | {\bf X}, {\bf w} ) = N \left( {\bf y} | f({\bf X}), \frac{1}{\beta}{\bf I} \right) = N \left( {\bf X}^{\rm T} {\bf w}, \frac{1}{\beta}{\bf I} \right) $$

2.2.2 線形回帰モデルのベイズ的解釈

　線形回帰モデルにおいて、 を推定する確率モデル の性能はパラメータ の値によって左右されます。確率モデル をベイズの枠組み:

$$ p({\bf w} | {\bf y}, {\bf X} ) = \frac{ p({\bf y} | {\bf X}, {\bf w}) p({\bf w}) } {p({\bf y} | {\bf X} )} = \frac{ p({\bf y} | {\bf X}, {\bf w}) p({\bf w}) } { \int p({\bf y} | {\bf X}, {\bf w}) p({\bf w}) ~ d{\bf w}} $$

によって拡張し、パラメータ の事後分布 を導出することで、N+1 番目の未知のデータサンプル に対する「ばらつきを持った確率モデル」である予測分布を導出しましょう。

（１） の事前分布

$$ p({\bf w}) = N \left( {\bf w} ~ | ~ {\bf 0}, ~ \frac{1}{\alpha} {\bf I} \right) $$

（２）尤度

$$ \begin{eqnarray} p({\bf y} | X, {\bf w}) & = &\prod_{i=1}^{N} p(y_i | {\bf x}_i, {\bf w}) \\ & = & \prod_{i=1}^{N} \frac{1}{ \sqrt{ 2 \pi \beta^{-1}}} \exp \left( - \frac{{\left( y_i - {{\bf x}_i}^{\rm T}{\bf w} \right)}^{2}}{2 \beta^{-1}} \right) \\ & = & \frac{1}{ {\left( 2 \pi \beta^{-1} \right)}^{n/2}} \exp \left( - \frac{{\left( {\bf y} - X^{\rm T}{\bf w} \right)}^{2}}{2 \beta^{-1}} \right) \\ & = & N \left( {\bf y} ~ | ~ X^{\rm T}{\bf w}, ~ \frac{1}{\beta}{\bf I} \right) \end{eqnarray} $$

（３） の事後分布

$$ \begin{eqnarray} p({\bf w} | {\bf X}, {\bf y}) & \propto & \exp \left( - \frac{1}{2} { ( {\bf y} - {\bf X}^{\rm T}{\bf w} ) }^{\rm T} { \left( \frac{1}{\beta} {\bf I} \right) }^{-1} ( {\bf y} - {\bf X}^{\rm T}{\bf w} ) \right) \exp \left( - \frac{1}{2} {\bf w}^{\rm T} { \left( \frac{1}{\alpha} {\bf I} \right) }^{-1} {\bf w} \right) \\ & \propto & \exp \left( { ( {\bf w} - {\hat{\bf w}}_{MAP} ) }^{\rm T} \left( \beta {\bf X}{\bf X}^{\rm T} + \alpha {\bf I} \right) ( {\bf w} - {\hat{\bf w}}_{MAP} ) \right) \\ & = & N \left( {\bf w} ~ | ~ {\hat{\bf w}}_{MAP}, ~ {\bf A}^{-1} \right) \end{eqnarray} $$

　ただし、

$$ \begin{eqnarray} {\hat{\bf w}}_{MAP} & := & \beta {\bf A }^{-1} {\bf X}{\bf y} \\ {\bf A} & := & \beta {\bf X}{\bf X}^{\rm T} + \alpha {\bf I} \end{eqnarray} $$

（４） の予測分布

$$ \begin{eqnarray} p^{*}(y^{*} | {\bf x}^{*}, {\bf X}, {\bf y}) & = & \int p(y^{*} | {\bf x}^{*}, {\bf w}) p( {\bf w} | X, {\bf y}) ~ d{\bf w} \\ & = & N \left( y^{*} ~|~ \beta {{\bf x}^{*}}^{\rm T} { \bf A }^{-1} {\bf X} {\bf y}, ~ { {\bf x}^{*}}^{\rm T} { \bf A }^{-1} {\bf x}^{*} \right) \end{eqnarray} $$

2.3 線形基底モデル

2.3.1 線形基底モデルの準備

　素朴な線形回帰モデルでは，入力ベクトル のあるデータ空間（data space） の中で，出力 を推定します．しかし，この場合，データ空間を構成する基底ベクトルの線形結合によって を推定するため, モデルの表現力が制約されてします。そこで，入力ベクトル を，基底関数（basis function） によって特徴量 へと変換し，高次元の特徴空間 （feature space）から の値を推定することを考えます．ここで，基底関数 による変換は線形でも非線形でもよいとします．

$$ {\bf x}_i \in \mathbb{R}^d \to \phi({\bf x}_i) \in \mathbb{R}^M \underset{\large \bf w}{\longrightarrow} f({\bf x}_i) \in \mathbb{R} \underset{ {\large \varepsilon_i} } {\longleftrightarrow} y_i \in \mathbb{R}, ~~~ (i=1, \dots, N) \\ $$

基底関数 は、データを表現する基底を変える（空間を変える）関数と考えることができます。また、一般に、 であることから、 はデータサンプルを高次元空間に写像する（mapping）関数であることがわかります。

• のデータ空間 における表現： $$ {\bf x}_i = \left( x_{i1}, x_{i2}, \dots, x_{id} \right) $$
• の特徴空間 における表現： $$ \phi({\bf x}_i) = \left( \phi_{1}({\bf x}_i), \phi_{2}({\bf x}_i), \dots, \phi_{M}({\bf x}_i) \right) $$

実際に，「線形基底モデル」を構築しましょう．モデルパラメータとして，重みベクトル を想定します．

$$ y_i = f({\bf x}_i) + \varepsilon_i \\ f({\bf x}_i) = { \phi ( {\bf x}_i ) }^{\rm T} {\bf w} = \left( \begin{array}{c} \phi_{1}({\bf x}_i), \dots, \phi_{M}({\bf x}_i) \end{array} \right) \cdot \left( \begin{array}{c} w_{1} \\ \vdots \\ w_{M} \end{array} \right), ~~~ \varepsilon_i \sim N \left( 0, \frac{1}{\beta} \right) $$

これらの関係式をまとめると、各 に対する の推定値は、次式のように「ばらつきを持った確率モデル」として表現されます。

$$ p( y_i | x_i, {\bf w} ) = N \left( y_i | f( {\bf x}_i ), \frac{1}{\beta} \right) = N \left( y_i | {\phi ( {\bf x}_i ) }^{\rm T} {\bf w}, \frac{1}{\beta} \right) $$

さらに、個々データではなくデータセット 全体に対して、回帰モデル はどのように作用するのかをまとめて考えます。計画行列（design matrix） と、ベクトル を以下のように定義します。

$$ \Phi({\bf X}) := \left( \phi({\bf x}_1), \phi({\bf x}_2), \dots, \phi({\bf x}_N) \right)= \left( \begin{array}{cccc} \phi_{1}({\bf x}_1) & \phi_{1}({\bf x}_2) & \dots & \phi_{1}({\bf x}_N) \\ \phi_{2}({\bf x}_1) & \phi_{2}({\bf x}_2) & \dots & \phi_{2}({\bf x}_N) \\ \vdots & \vdots & \dots & \vdots \\ \phi_{M}({\bf x}_1) & \phi_{M}({\bf x}_2) & \dots & \phi_{M}({\bf x}_N) \end{array} \right), ~~~ {\bf y} := \left( \begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_N \end{array} \right), ~~~ {\boldsymbol \varepsilon} := \left( \begin{array}{c} \varepsilon_1 \\ \varepsilon_2 \\ \vdots \\ \varepsilon_N \end{array} \right) $$

すると、「線形基底回帰モデル」は以下のように記述され、

$$ {\bf y} = f({\bf X}) + {\boldsymbol \varepsilon}, \\ f({\bf X}) = {\Phi({\bf X})}^{\rm T}{\bf w}, ~~~ \boldsymbol \varepsilon \sim N \left( {\bf 0}, \frac{1}{\beta}{\bf I}\right) $$

これらの関係式をまとめると、 データセット における の推定値は、次式のように「ばらつきを持った確率モデル」として表現されます。

$$ p( {\bf y} | {\bf X}, {\bf w} ) = N \left( {\bf y} ~|~ f({\bf X}), \frac{1}{\beta}{\bf I} \right) = N \left( {\bf y} ~|~ {\Phi({\bf X})}^{\rm T}{\bf w}, \frac{1}{\beta}{\bf I} \right) $$

2.3.2 線形基底モデルのベイズ的解釈

　確率モデル をベイズの枠組み:

$$ p({\bf w} | {\bf y}, {\bf X} ) = \frac{ p({\bf y} | {\bf X}, {\bf w}) p({\bf w}) } {p({\bf y} | {\bf X} )} = \frac{ p({\bf y} | {\bf X}, {\bf w}) p({\bf w}) } { \int p({\bf y} | {\bf X}, {\bf w}) p({\bf w}) ~ d{\bf w}} $$

によって拡張し、パラメータ の事後分布 を導出することで、N+1 番目の未知のデータサンプル に対する「ばらつきを持った確率モデル」である予測分布を導出しましょう。

（１） の事前分布

$$ p({\bf w}) = N \left( {\bf w} ~ | ~ {\bf 0}, ~ \frac{1}{\alpha} {\bf I} \right) $$

（２）尤度

$$ \begin{eqnarray} p({\bf y} | \Phi({\bf X}), {\bf w}) & = &\prod_{i=1}^{N} p(y_i | \phi({\bf x}_i), {\bf w}) \\ & = & \prod_{i=1}^{N} \frac{1}{ \sqrt{ 2 \pi \beta^{-1}}} \exp \left( - \frac{{\left( y_i - {\phi({\bf x}_i)}^{\rm T}{\bf w} \right)}^{2}}{2 \beta^{-1}} \right) \\ & = & \frac{1}{ {\left( 2 \pi \beta^{-1} \right)}^{n/2}} \exp \left( - \frac{{\left( {\bf y} - {\Phi({\bf X})}^{\rm T}{\bf w} \right)}^{2}}{2 \beta^{-1}} \right) \\ & = & N \left( {\bf y} ~ | ~ {\Phi({\bf X})}^{\rm T}{\bf w}, ~ \frac{1}{\beta}{\bf I} \right) \end{eqnarray} $$

（３） の事後分布

$$ \begin{eqnarray} p({\bf w} | \Phi({\bf X}), {\bf y}) & \propto & \exp \left( - \frac{1}{2} { ( {\bf y} - {\Phi({\bf X})}^{\rm T}{\bf w} ) }^{\rm T} { \left( \frac{1}{\beta} {\bf I} \right) }^{-1} ( {\bf y} - {\Phi({\bf X})}^{\rm T}{\bf w} ) \right) \exp \left( - \frac{1}{2} {\bf w}^{\rm T} { \left( \frac{1}{\alpha} {\bf I} \right) }^{-1} {\bf w} \right) \\ & \propto & \exp \left( { ( {\bf w} - {\hat{\bf w}}_{MAP} ) }^{\rm T} \left( \beta {\Phi({\bf X})}{\Phi({\bf X})}^{\rm T} + \alpha {\bf I} \right) ( {\bf w} - {\hat{\bf w}}_{MAP} ) \right) \\ & = & N \left( {\bf w} ~ | ~ {\hat{\bf w}}_{MAP}, ~ { A }^{-1} \right) \end{eqnarray} $$

　ただし、

$$ \begin{eqnarray} {\hat{\bf w}}_{MAP} & := & \beta { \bf A }^{-1} {\bf X}{\bf y} \\ A & := & \beta {\Phi({\bf X})}{\Phi({\bf X})}^{\rm T} + \alpha {\bf I} \end{eqnarray} $$

（４） の予測分布

$$ \begin{eqnarray} p^{*}(y^{*} | {\bf x}^{*}, \Phi({\bf X}), {\bf y}) & = & \int p(y^{*} | {\bf x}^{*}, {\bf w}) p( {\bf w} | \Phi({\bf X}), {\bf y}) ~ d{\bf w} \\ & = & N \left( y^{*} ~|~ \beta {{\bf x}^{*}}^{\rm T} { \bf A}^{-1} \Phi({\bf X}) {\bf y}, ~ { {\bf x}^{*}}^{\rm T} { \bf A}^{-1} {\bf x}^{*} \right) \end{eqnarray} $$

2.4 ガウス過程による線形基底モデルの表現

2.4.1 ガウス過程による回帰モデルの準備

　ガウス過程による回帰では、基底関数 ではなく、回帰モデル の確率分布 の共分散行列 を事前に定めます。 をグラム行列（Gram Matrix）といいます。

$$ {\bf K}_{XX} = \left( \begin{array}{cccc} k({\bf x}_1, {\bf x}_1) & k({\bf x}_1, {\bf x}_2) & \dots & k({\bf x}_1, {\bf x}_N) \\ k({\bf x}_2, {\bf x}_1) & k({\bf x}_2, {\bf x}_2) & \dots & k({\bf x}_2, {\bf x}_N) \\ \vdots & \vdots & \ddots & \vdots \\ k({\bf x}_N, {\bf x}_1) & k({\bf x}_N, {\bf x}_2) & \dots & k({\bf x}_N, {\bf x}_N) \\ \end{array} \right) $$ ただし、 $$ \begin{eqnarray} k({\bf x}_i, {\bf x}_j) & = & C o v \left[ f( {\bf x}_i ), f( {\bf x}_j ) \right] \\ & = & { \phi( {\bf x}_i )}^{\rm T} \left( \frac{1}{\alpha} {\bf I} \right) \phi( {\bf x}_j ) \\ & = & \frac{1}{\alpha} \phi_{1}( {\bf x}_i ) \phi_{1}( {\bf x}_j ) + \cdots + \frac{1}{\alpha} \phi_{M}( {\bf x}_i ) \phi_{M}( {\bf x}_j ) \end{eqnarray} $$

　定義から、グラム行列 は と の分散からなる行列（=共分散行列）です。すなわち、グラム行列 は、基底関数（basis function） と計画行列（design matrix） および重みベクトル の事前分布 によっても記述されます。

$$ \begin{eqnarray} {\bf K}_{XX} & = & \left( \begin{array}{cccc} C o v \left[ f({\bf x}_1), f({\bf x}_1) \right] & C o v \left[ f({\bf x}_1), f({\bf x}_2) \right] & \dots & C o v \left[ f({\bf x}_1), f({\bf x}_N) \right] \\ C o v \left[ f({\bf x}_2), f({\bf x}_1) \right] & C o v \left[ f({\bf x}_2), f({\bf x}_2) \right] & \dots & C o v \left[ f({\bf x}_2), f({\bf x}_N) \right] \\ \vdots & \vdots & \ddots & \vdots \\ C o v \left[ f({\bf x}_N), f({\bf x}_1) \right] & C o v \left[ f({\bf x}_N), f({\bf x}_2) \right] & \dots & C o v \left[ f({\bf x}_N), f({\bf x}_N) \right] \\ \end{array} \right) \\ \\ & = & {\Phi({\bf X})}^{\rm T} \left( \frac{1}{\alpha}{\bf I} \right) \Phi({\bf X}) \\ & = & \frac{1}{\alpha} \Phi({\bf X}) { \Phi({\bf X}) }^{\rm T} \end{eqnarray} $$

すなわち、同一の線形基底モデルは，以下の2つの視点から記述することが可能です．ガウス過程を含む「カーネル法」は，後者の関数空間による視点（function space view）に根ざした多変量解析手法です．

1. 基底関数 と計画行列 によって表現する（weight space view）
   • モデル設計者は，基底関数 を事前に定める．
2. グラム行列 によって表現する（function space view）
   • モデル設計者は，カーネル関数 を事前に定める．

以上より，モデルの出力値 と変数 の確率分布は，次のように導出されます，

$$ \begin{eqnarray} p \bigl( f({\bf X}) \bigr) & = & N \left( f({\bf X}) ~|~ {\bf 0}, \frac{1}{\alpha}\Phi({\bf X}) {\Phi({\bf X})}^{\rm T} \right) \\ & = & N \Bigl( f({\bf X}) ~|~ {\bf 0}, {\bf K}_{XX} \Bigr) \\ \\ p \bigl( {\bf y} \bigr) & = & N \left( {\bf y} ~|~ {\bf 0}, \frac{1}{\alpha}\Phi({\bf X}) {\Phi({\bf X})}^{\rm T} + \frac{1}{\beta} {\bf I} \right) \\ & = & N \Bigl( {\bf y} ~|~ {\bf 0}, {\bf K}_{XX} + \frac{1}{\beta} {\bf I} \Bigr) \\ \end{eqnarray} $$

2.4.2 ガウス過程による回帰モデルによる予測

　ここで、N+1 番目の未知のデータ に対する の予測値 を導出しましょう。

$$ y^{*} = f( {\bf x}^{*} ) + {\varepsilon}^{*} \\ f( {\bf x}^{*} ) = { \phi( {\bf x}^{*} ) }^{\rm T} {\bf w}, ~~~ {\varepsilon}^{*} \sim N \left( 0, \frac{1}{\beta} \right) $$

2.3.2 の結果から、 の予測分布は以下のように記述されます。

$$ f ( {\bf x}^{*} ) \sim N \Bigl( \mathbb{E} \left[ f ( {\bf x}^{*} ) \right] , \mathbb{V} \left[ f ( {\bf x}^{*} ) \right] \Bigr) $$ $$ \begin{eqnarray} \left\{ \begin{array}{c} \mathbb{E} \left[ f ( {\bf x}^{*} ) \right] & = & { {\bf k}^{*} }^{\rm T} { \left( {\bf K}_{XX} + \frac{1}{\beta} {\bf I} \right) }^{-1} {\bf y} \\ \mathbb{V} \left[ f ( {\bf x}^{*} ) \right] & = & k ( {\bf x}^{*}, {\bf x}^{*} ) - { {\bf k}^{*} }^{\rm T} { \left( {\bf K}_{XX} + \frac{1}{\beta} {\bf I} \right) }^{-1} {\bf k}^{*} \end{array} \right. \end{eqnarray} $$

未知のデータ をガウス過程 に加えると、

$$ \begin{eqnarray} {{\bf K}_{XX}}^{*} & = & \left( \begin{array}{cccc} k( {\bf x}_1, {\bf x}_1 ) & \dots & k( {\bf x}_1, {\bf x}_N ) & k( {\bf x}_1, {\bf x}^{*} ) \\ \vdots & \ddots & \vdots & \vdots \\ k( {\bf x}_N, {\bf x}_1 ) & \dots & k( {\bf x}_N, {\bf x}_N ) & k( {\bf x}_N, {\bf x}^{*} ) \\ k( {\bf x}^{*}, {\bf x}_1 ) & \dots & k( {\bf x}^{*}, {\bf x}_N ) & k( {\bf x}^{*}, {\bf x}^{*} ) \\ \end{array} \right) \\ \\ & = & \left( \begin{array}{cc} {\bf K}_{XX} & {\bf k}^{*} \\ { {\bf k}^{*} }^{\rm T} & k( {\bf x}^{*}, {\bf x}^{*} ) \end{array} \right) \end{eqnarray} $$

ただし、 は以下のように記述されるベクトルです。 $$ \begin{eqnarray} {\bf k}^{*} & := & \left( \begin{array}{c} k( {\bf x}_1, {\bf x}^{*} ) \\ \vdots \\ k( {\bf x}_N, {\bf x}^{*} ) \end{array} \right) \\ \\ & = & \left( \begin{array}{c} C o v \left[ f( {\bf x}_1 ), f( {\bf x}^{*} ) \right] \\ \vdots \\ C o v \left[ f( {\bf x}_N ), f( {\bf x}^{*} ) \right] \end{array} \right) \\ \\ & = & \left( \begin{array}{c} { \phi( {\bf x}_1 )}^{\rm T} \left( \frac{1}{\alpha} {\bf I} \right) \phi( {\bf x}^{*} ) \\ \vdots \\ { \phi( {\bf x}_N )}^{\rm T} \left( \frac{1}{\alpha} {\bf I} \right) \phi( {\bf x}^{*} ) \end{array} \right) \\ \\ & = & \left( \begin{array}{c} \frac{1}{\alpha} \phi_{1}( {\bf x}_1 ) \phi_{1}( {\bf x}^{*} ) + \cdots + \frac{1}{\alpha} \phi_{M}( {\bf x}_1 ) \phi_{M}( {\bf x}^{*} ) \\ \vdots \\ \frac{1}{\alpha} \phi_{1}( {\bf x}_N ) \phi_{1}( {\bf x}^{*} ) + \cdots + \frac{1}{\alpha} \phi_{M}( {\bf x}_N ) \phi_{M}( {\bf x}^{*} ) \end{array} \right) \\ \\ & = & { \phi( {\bf x}^{*} ) }^{\rm T} \frac{1}{\alpha} {\bf I} ~ \Phi( {\bf X} ) \end{eqnarray} $$

3. ガウス過程回帰をPythonで実装

　実際に、ある関数からデータサンプルを作成して、ガウス過程による回帰モデル によってこれを近似します。今回は、以下のような平均関数 と共分散関数 を用いたガウス過程 と、それに従う回帰モデル を考えます。ここで、共分散関数としてRBFカーネル（Radial basis function kernel, Gaussian kernel）を採用しています。

$$ f(x) \sim \mathcal{GP} \left( m(x), k(x, x') \right) $$

この回帰モデルを用いて、関数：

$$ y = \sin(2 \pi x) + \cos(1.7 \times 2 \pi x) ~~~ (0 \leq x \leq 1) $$

を、生成されるデータサンプルから予測してみましょう。なお実装は、こちらのQuitta記事を参考にさせてもらいました。

3.1 RBFカーネルのためのクラス

class RBFKernel(object):
    
    def __init__(self, sigma):
        self.sigma = sigma
        
    def get_sigma(self):
        return np.copy(self.sigma)

    def __call__(self, x1, x2):
        return np.exp( (-1. / (self.sigma ** 2) ) *  (x1 - x2) ** 2)

    def derivatives(self, x1, x2):
        dif_sigma = np.exp( (-1. / (self.sigma ** 2) ) *  (x1 - x2) ** 2) * ( (x1 - x2) ** 2 ) / ( self.sigma ** 3)
        return dif_sigma

    def update_sigma(self, update):
        self.sigma += update

3.2 ガウス過程回帰を行うためのクラス

class GaussianProcessRegression(object):

    def __init__(self, kernel, x, y, beta=1.):
        self.kernel = kernel
        self.x = x
        self.y = y
        self.beta = beta
        
        # グラム行列を計算
        self.fit_kernel()

    def fit_kernel(self):
        ''' グラム行列を計算 '''
        
        # グラム行列 K
        self.gram = self.kernel(*np.meshgrid(self.x, self.x))
        # 共分散行列 K + 1/beta I
        self.covariance = self.gram + np.identity(len(self.x)) / self.beta
        # 精度行列 (共分散行列の逆行列)
        self.precision = np.linalg.inv(self.covariance)
    
    def predict_y(self, x_new):
        ''' y_new の予測値と分散を出力 '''
        
        # k*
        k = np.array([self.kernel(xi, x_new) for xi in self.x])

        # 平均と分散
        y_mean = k.dot(self.precision.dot(self.y))
        y_var = self.kernel(x_new, x_new) - k.dot(self.precision.dot(k))
        
        return y_mean, y_var

3.3 グラフの描画（100フレームのアニメーション）を作成する

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation

def func(x):
    ''' 回帰モデルによって近似を行う関数 '''
    return np.sin(2 * np.pi * x) + np.cos(1.7 * 2 * np.pi * x)


def create_data_sample(func, low=0, high=1., n=10, std=1.):
    ''' n 組のデータサンプル (x, y) を作成する '''
    x = np.random.uniform(low, high, n)
    y = func(x) + np.random.normal(scale=std, size=n)
    return x, y
    
def _update(frame, x_data, y_data):
    ''' フレームごとにグラフを描画する '''
        
    # 現在のグラフを消去する
    plt.cla()
    
    # データサンプルのframe数分の取得
    x = x_data[:frame]
    y = y_data[:frame]
    
    # 回帰モデルをつくる
    kernel = RBFKernel(sigma=0.5)
    regression = GaussianProcessRegression(kernel, x, y, beta=100)
    
    # 描画用にxのデータを生成
    x_test = np.linspace(0, 1, 100)
    
    # yの予測値の平均と分散を導出
    y_test=[]
    y_var=[]
    for x_new in x_test:
        y_new_mean, y_new_var = regression.predict_y(x_new)
        y_test.append(y_new_mean)
        y_var.append(y_new_var)
        
    # list を numpy.ndarrayに変換
    y_test = np.array(y_test)
    y_var = np.array(y_var)
    
    # グラフを描画
    plt.scatter(x, y, alpha=0.4, color="blue", label="data sample")
    plt.plot(x_test, func(x_test), color="blue", linestyle="dotted", label="actual function")
    plt.plot(x_test, y_test, color="red", label="predicted function")
    plt.fill_between(x_test, y_test - 3 * np.sqrt(y_var), y_test + 3 * np.sqrt(y_var), color="pink", alpha=0.5, label="95% confidence interval (2 * std)")
    plt.legend(loc="lower left")
    plt.xlabel("x")
    plt.ylabel("y")
    plt.xlim([-0, 1])
    plt.ylim([-2.1, 2.1])
    plt.title("Gaussian Process Regression \n (RBF kernel, sigma=0.5, sample size = " + str(frame) + ")")
    
def main():
    # 描画領域
    fig = plt.figure(figsize=(8, 6))

    # データサンプルを作成
    x_data, y_data = create_toy_data(func, low=0, high=1, n=100, std=0.1)

    params = {
        'fig': fig,
        'func': _update,  # グラフを更新する関数
        'fargs': (x_data, y_data),  # 関数の引数 (フレーム番号を除く)
        'interval': 1,  # 更新間隔 (ミリ秒)
        'frames': np.arange(1, 101, 1),  # フレーム番号を生成するイテレータ, 1~100
        'repeat': False,  # 繰り返さない
    }

    # アニメーションを作成する
    ani = animation.FuncAnimation(**params)

    # アニメーションを保存する
    ani.save("./gpr_rbf.gif")
    # アニメーションを表示する
    # plt.show()

3.4 結果：アニメーションの描画

　 　サンプルサイズ（データ点の数）が増えると、徐々に回帰モデルで予測した関数（predicted function）が真の関数（actual function）に近づいていることがわかります。

4. 参考書籍

Gaussian Processes for Machine Learning (Adaptive Computation and Machine Learning series)

Pattern Recognition and Machine Learning (Information Science and Statistics)

ガウス過程の基礎 - 赤穂昭太郎, 2018

指数分布とワイブル分布をPythonでプロットしてみる

　生存時間解析など、応用範囲の広い指数分布についてまとめます。指数型分布族の仲間としては、ワイブル分布・ガンマ分布の他にも、ポアソン分布、レイリー分布、ラプラス分布（両側指数分布）などがあります。

1. 前提

1.1 確率分布の定義

　指数分布の確率密度関数 と累積分布関数 は、次のように定義されます。

• 指数分布

$$ X \sim Exp(\lambda), ~~~ \lambda \geq 0 $$

$$ \begin{eqnarray} f(x | \lambda) & = & \lambda ~ exp \left( - \lambda x \right) ~~~ (x \geq 0) \\ F(x | \lambda) & = & 1 - exp \left( - \lambda x \right) ~~~ (x \geq 0) \\ \end{eqnarray} $$ $$ \begin{eqnarray} \mathbb{E}\left[ X \right] & = & \frac{1}{\lambda} \\ \mathbb{V}\left[ X \right] & = & \frac{1}{\lambda^{2}} \end{eqnarray} $$

　また、ワイブル分布は、次のように定義されます。なお、 は、ガンマ関数*1（階乗を一般化したもの）です。

• ワイブル分布

$$ X \sim Weibull(\alpha, \beta), ~~~ \alpha \geq 0, ~~~ \beta \geq 0 $$

$$ \begin{eqnarray} f(x | \alpha, \beta) & = & \frac{\alpha}{\beta} { \left( \frac{x}{\beta} \right) }^{\alpha - 1} \left\{ - { \left( \frac{x}{\beta} \right) }^{\alpha} \right\} ~~~ (x \geq 0) \\ F(x | \alpha, \beta) & = & 1 - exp\left\{ - {\left( \frac{x}{\beta} \right) }^{a} \right\} ~~~ (x \geq 0) \\ \end{eqnarray} $$ $$ \begin{eqnarray} \mathbb{E}\left[ X \right] & = & \beta ~ \Gamma \left( 1 + \frac{1}{\alpha} \right) \\ \mathbb{V}\left[ X \right] & = & \beta^{\large \frac{2}{\alpha}} \left\{ \Gamma(1 + \frac{2}{\alpha}) - {\left( \Gamma(1 + \frac{1}{\alpha}) \right)}^{2} \right\} \end{eqnarray} $$

1. 2 指数分布とワイブル分布の関係

　ワイブル分布のパラメータをそれぞれ とすると指数分布に一致します。つまり、ワイブル分布は、指数分布の一般に拡張したものになります。

$$ Exp(\lambda) = Weibull(1, \frac{1}{\lambda}) $$

ちなみに、以下で定義されるガンマ分布のパラメータをそれぞれ とすると指数分布に一致します。

$$ Exp(\lambda) = Weibull(1, \frac{1}{\lambda}) = Gamma(1, \frac{1}{\lambda}) $$

• ガンマ分布

$$ X \sim Gamma(\alpha, \beta) $$

$$ \begin{eqnarray} f(x | \alpha, \beta) & = & \frac{1}{\Gamma(\alpha)} \frac{1}{\beta} {\left( \frac{x}{\beta} \right) }^{\alpha - 1}~~~ (x \gt 0) \\ \end{eqnarray} $$ $$ \begin{eqnarray} \mathbb{E}\left[ X \right] & = & \alpha \beta \\ \mathbb{V}\left[ X \right] & = & \alpha {\beta}^{2} \end{eqnarray} $$

2. Pythonによる実装

2.1 指数分布

python で分布を定義して、グラフをプロットしてみます。

import math
import random
import numpy as np
import matplotlib.pyplot as plt

# 指数分布

class Exp():
    def __init__(self):
        pass
    
    # 密度関数f
    def f(self, x, la=1):
        return la * math.exp(-1 * la * x)
    
    # 分布関数F
    def F(self, x, la=1):
        return 1 - math.exp(-1 * la * x)
    
    # Fの逆関数(samplingに使う)
    def invF(self, y, la=1):
        return -1 * (1 / la) * math.log(1 - y)
    
    # サンプリング
    def sampling(self, num, la):
        sample=[]
        for i in range(num):
            rand = random.random()
            sample.append(self.invF(rand, la))
        return np.array(sample)
    
    # 散布図
    def scatter_pdf(self, ax, data, la, alpha=0.4):
        pdf=[]
        for d in data:
            pdf.append(self.f(d, la))

        ax.scatter(data, pdf, alpha=alpha)
        ax.set_title("Exponential (lambda={:.2f})".format(la))
        ax.set_xlabel("value")
        ax.set_ylabel("probability density")
        ax.set_ylim(0, 1)
        
    # グラフ
    def plot_pdf(self, ax, data, la):
        pdf=[]
        for d in data:
            pdf.append(self.f(d, la))

        ax.plot(data, pdf)
        ax.set_title("Exponential (lambda={:.2f})".format(la))
        ax.set_xlabel("value")
        ax.set_ylabel("probability density")
        ax.set_ylim(0, 1)

実際にグラフを描画してみます。パラメータ の値を変えて、分布の形状をみます。

# グラフをmatplotlibで描画してみる

data = np.linspace(0, 15, 100)

fig, ax = plt.subplots(3, 3, figsize=(18, 18))

Exp().plot_pdf(ax[0, 0], data, 0.2)
Exp().plot_pdf(ax[0, 1], data, 0.4)
Exp().plot_pdf(ax[0, 2], data, 0.6)
Exp().plot_pdf(ax[1, 0], data, 0.8)
Exp().plot_pdf(ax[1, 1], data, 1)
Exp().plot_pdf(ax[1, 2], data, 1.2)
Exp().plot_pdf(ax[2, 0], data, 1.4)
Exp().plot_pdf(ax[2, 1], data, 1.6)
Exp().plot_pdf(ax[2, 2], data, 1.8)

plt.show()

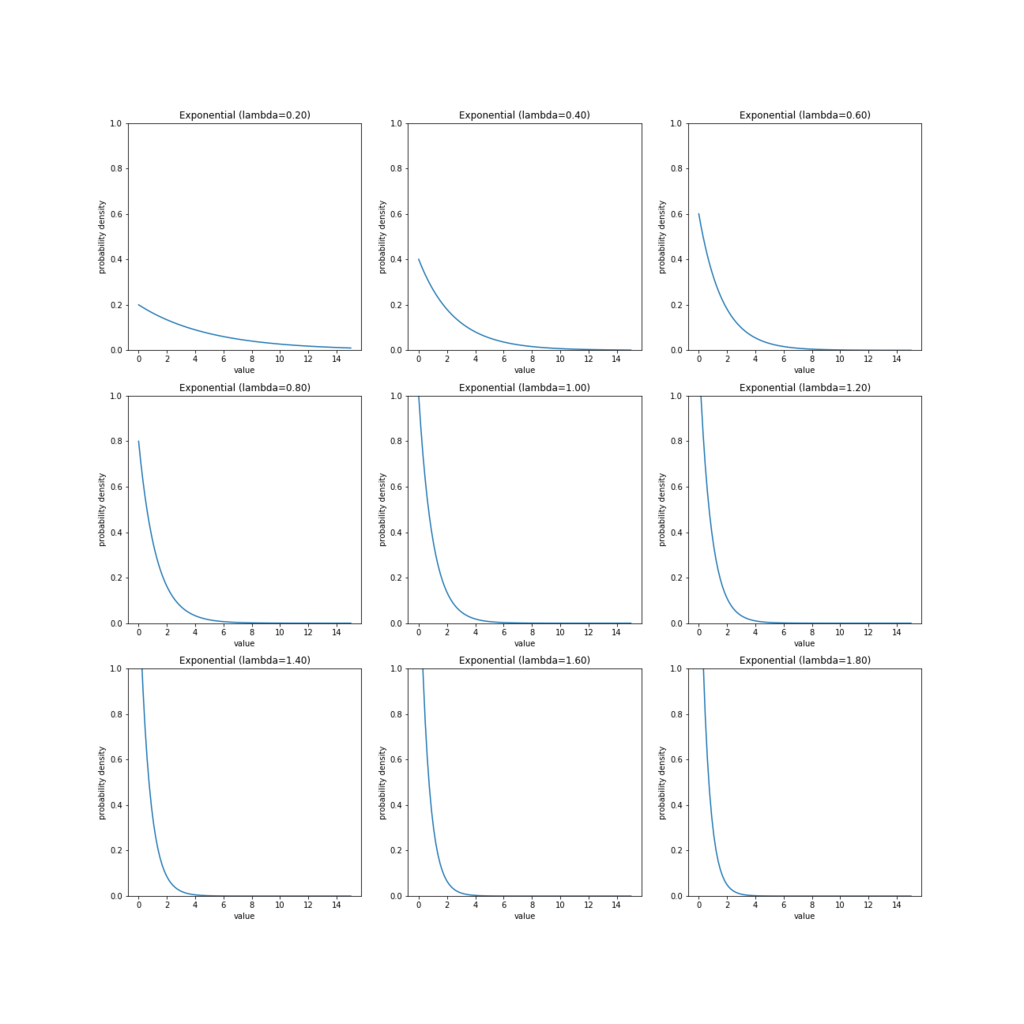
　プロットをみると、指数分布のパラメータ は、尺度（ばらつき）を表していることがわかります。分布は が大きくなるにつれ急峻になり、ばらつきが少なくなっていきます。平均について 、分散について となることから、「指数分布はパラメータ を上げると、平均は０に接近し、分散は限りなく小さくなる（０になる）」ということがわかります。

2.2 ワイブル分布

python で分布を定義して、グラフをプロットしてみます。

import math
import random
import numpy as np
import matplotlib.pyplot as plt

# ワイブル分布

class Weibull():
    def __init__(self):
        pass
        
    # 密度関数f
    def f(self, x, a, b):
        return (a/b) * ( (x/b)**(a - 1) ) * math.exp(-1 * (x/b)**a )
    
    # 分布関数F
    def F(self, x, a, b):
        return 1 - math.exp(-1 * (x/b)**a )
    
    # Fの逆関数
    def invF(self, y, a, b):
        return b * ( -1 * math.log(1 - y) )**(1/a)
    
    # サンプリング
    def sampling(self, num, a, b):
        sample=[]
        for i in range(num):
            rand = random.random()
            sample.append(self.invF(rand, a, b))
        return np.array(sample)
    
    # 散布図
    def scatter_pdf(self, ax, data, a, b, alpha=0.4):
        pdf=[]
        for d in data:
            pdf.append(self.f(d, a, b))

        ax.scatter(data, pdf, alpha=alpha)
        ax.set_title("Weibull (alpha={:.2f}, beta={:.2f})".format(a, b))
        ax.set_xlabel("value")
        ax.set_ylabel("probability density")
        ax.set_ylim(0, 1)
        
    # グラフ
    def plot_pdf(self, ax, data, a, b):
        pdf=[]
        for d in data:
            pdf.append(self.f(d, a, b))

        ax.plot(data, pdf)
        ax.set_title("Weibull (alpha={:.2f}, beta={:.2f})".format(a, b))
        ax.set_xlabel("value")
        ax.set_ylabel("probability density")
        ax.set_ylim(0, 1)

実際にグラフを描画してみます。パラメータ の値を変えて、分布の形状をみます。

# グラフをmatplotlibで描画してみる

data = np.linspace(0, 15, 100)

fig, ax = plt.subplots(3, 3, figsize=(18, 18))

Weibull().plot_pdf(ax[0, 0], data, 1, 1)
Weibull().plot_pdf(ax[0, 1], data, 1, 2)
Weibull().plot_pdf(ax[0, 2], data, 1, 3)
Weibull().plot_pdf(ax[1, 0], data, 2, 1)
Weibull().plot_pdf(ax[1, 1], data, 2, 2)
Weibull().plot_pdf(ax[1, 2], data, 2, 3)
Weibull().plot_pdf(ax[2, 0], data, 3, 1)
Weibull().plot_pdf(ax[2, 1], data, 3, 2)
Weibull().plot_pdf(ax[2, 2], data, 3, 3)

plt.show()

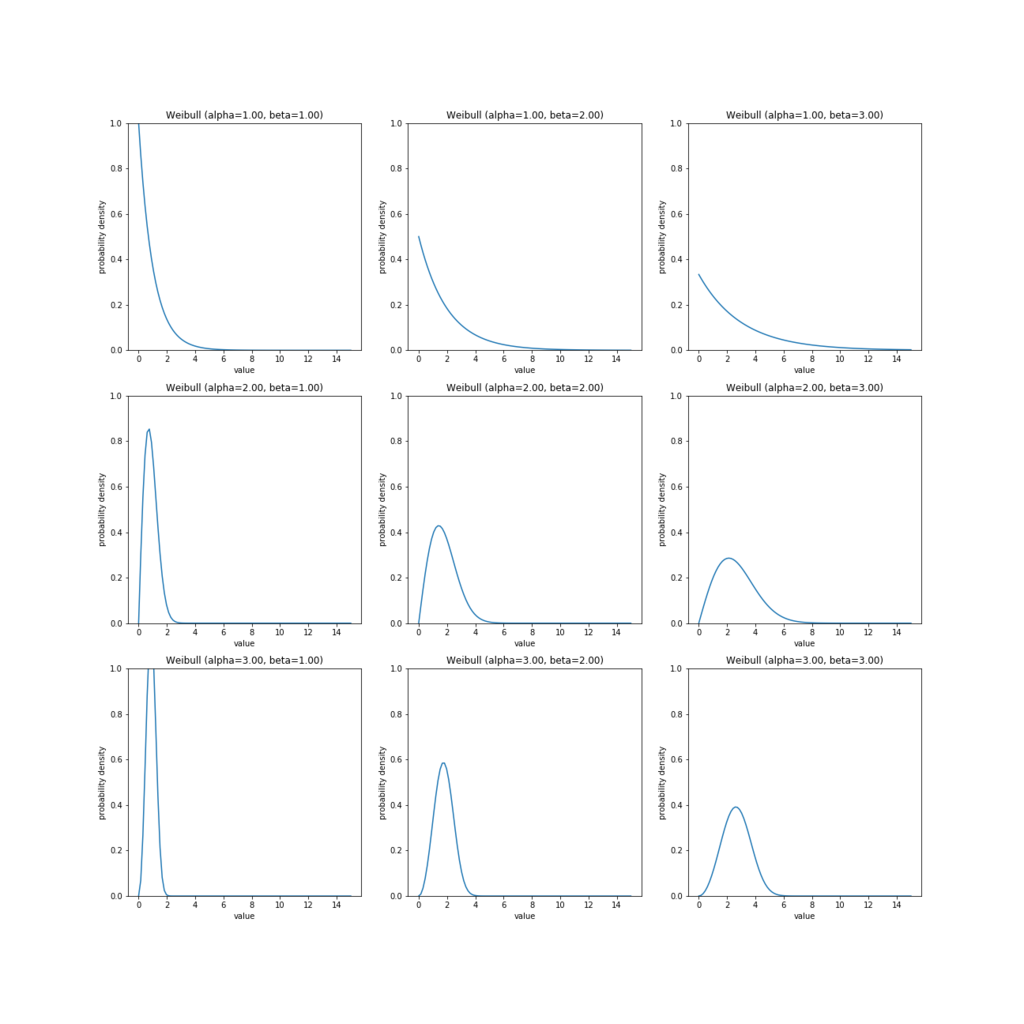
　プロットをみると、ワイブル分布のパラメータ は分布の形状を表し、パラメータ は、尺度（ばらつき）を表していることがわかります。実際、分布の形状は によって支配されており、ワイブル分布は のとき指数分布、 のときレイリー分布と一致します。分布は が大きくなるにつれ急峻になり、ばらつきが少なくなっていきます。

*1:ガンマ関数は、$$ \Gamma(n):=\int_{0}^{\infty} y^{n - 1} e^{-y} dy $$と定義され、 が自然数ならば が成り立つ。

Kullback-Leibler Divergenceについてまとめる

!! お知らせ（2020.06.10） * こちらの記事の英語版を公開しました．よければご覧ください．
Here is the english translation of this post. Please check it if you want.

1. KL-divergenceとは?

　統計学や情報理論をはじめとした広い分野で、KL-divergence*1はたびたび登場します。KL-divergenceは、「尤度比（尤もらしさを比較する尺度）を log 変換し（乗算操作を線形結合に直す、凸関数だから最適化との相性良い）、期待値（確率密度の重み付きの積分、ルベーグ積分）をとったもの」として定義されます。

1.1 定義

　一般に、確率分布 が確率密度関数 をもつとき、KL-divergence（Kullback-Leibler divergence）は、以下のように定義されます。

\begin{eqnarray} D_{KL}( Q \mid\mid P ) := \int q(x) \log \frac{q(x)}{p(x)} ~dx \tag{1} \end{eqnarray}

1.2 基本的な性質

　KL-divergenceは以下のような性質をもちます。

• （非負性）非負の値域をもつ。

\begin{align} 0 \leq D_{KL}( Q \mid\mid P ) \leq \infty \tag{2.1} \end{align}

• （完備性）値が 0 のとき、2つの確率分布 P と Q は同等。

\begin{align} D_{KL}( Q \mid\mid P ) = 0 ~~ \Leftrightarrow ~~ P = Q \tag{2.2} \end{align}

• （非対称性）値は P と Q に対して対称性を持たない。

\begin{align} D_{KL}( Q \mid\mid P ) \neq D_{KL}( P \mid\mid Q ) \tag{2.3} \end{align}

• （絶対連続性）値が発散しない限り、Q は P に関して絶対連続である。

\begin{align} D_{KL}( Q \mid\mid P ) \lt \infty ~~ \Rightarrow ~~ P \gg Q \tag{2.4} \end{align}

　例として、2つの正規分布間でKL-divergenceを計算*2すると、以下のような値になります。分布のズレが大きくなるほど、値が増加していることがわかります。

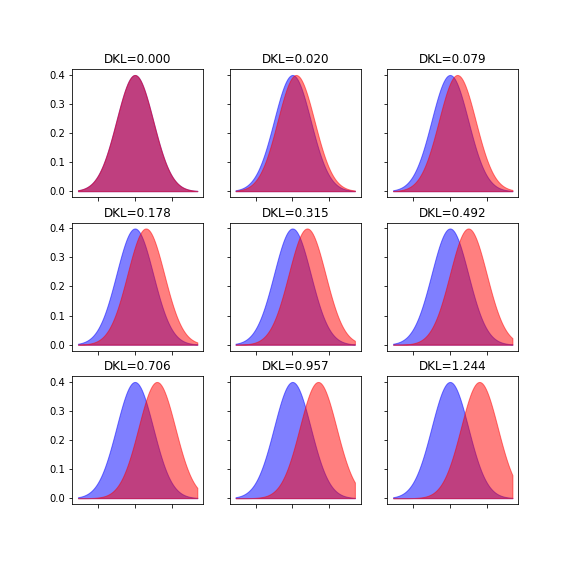
1.3 KL-divergenceは距離なのか？

　KL-divergenceは、確率や情報を考える際にとても重要な量であるため、分野や文脈によって様々な名称で呼ばれます。

"KL-divergence"
"KL-metrics"
"KL-information"
"Information divergence"
"Information gain"
"Relative entropy"

　KL-divergenceはつねに非負の値をとるため、これは確率分布 P と Q が存在する空間における距離(metrics)を示していると解釈することができます。しかし、KL-divergenceは次の距離の公理のうち「非負性」と「完備性」しか満たさないため、厳密には 距離(metrics) ではありません。

距離 の公理

1. 非負性　　　　
2. 完備性　　　　
3. 対称性　　　　
4. 三角不等式　　

　例えば、ユークリッド距離、二乗距離、マハラビノス距離、ハミング距離などは、この4つの条件をすべて満たすため、明らかに距離(metrics)として扱うことができます。一方で、KL-divergenceは距離(metrics)ではなくdivergenceです。"divergence"とは、距離の公理における４つの条件のうち「非負性」「対称性」のみを採用したものであり、"距離(metrics)"の拡張概念です。距離の公理による制約を減らし、抽象度の高い議論をしようというわけです。

　なお、このdivergenceという語は発散と訳されることが一般的で、例えば物理学ではベクトル作用素 div として登場します。divergenceのイメージに該当する日本語はありませんが、相違度、分離度、逸脱度、乖離度などが使われているようです。

　実例として、2つの正規分布 （青）と （赤）の間のKL-divergenceを測ってみましょう。左が青からみた赤とのKL距離、右が赤からみた青とのKL距離となっており値が異なることがわかります。なお「等分散正規分布間のKL-divergence」という特殊な条件下では、対称性が成り立ちます。

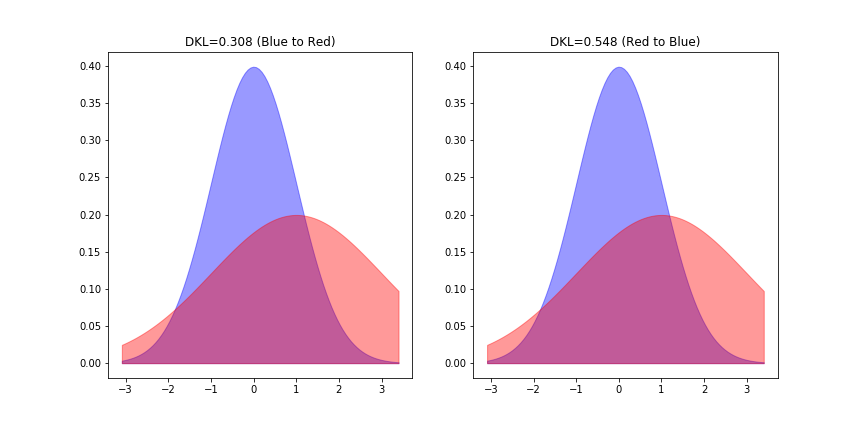
また，確率分布間の近さを測る尺度としては，KL情報量の他にも次のようなものが知られています．

確率分布 間の"距離"を測る量

• 　　　　　　　　 統計量

• 　　　　　　 -ノルム

• 　　　　　 -ノルム

• 　　 ヘリンジャー距離

• 　　　　　　 -ダイバージェンス 　

• 　 　 一般化情報量(Kawada, 1987)

• 　　 　　 KL情報量

2. 諸量との関係

2.1 KL-divergenceと相互情報量

　エントロピー 、結合エントロピー 、条件つきエントロピー 、相互情報量 は、確率密度 を用いて以下のように定義されます。*3

\begin{align} H(X) & := - \int Pr(x) \log Pr(x) ~dx \tag{3.1} \\ H(X,Y) & := - \int Pr(x,y) \log Pr(x,y) ~dy~dx \tag{3.2} \\ H(X|Y) & := - \int Pr(x,y) \log Pr(x|y) ~dx~dy \tag{3.3} \\ MI(X,Y) & := \int \int Pr(x,y) \log \frac{Pr(x,y)}{Pr(x)Pr(y)} ~dxdy \tag{3.4} \end{align}

2つの確率変数 X, Y について、相互情報量 MI（: Mutual Information）によって相互の関係性が明示されます。

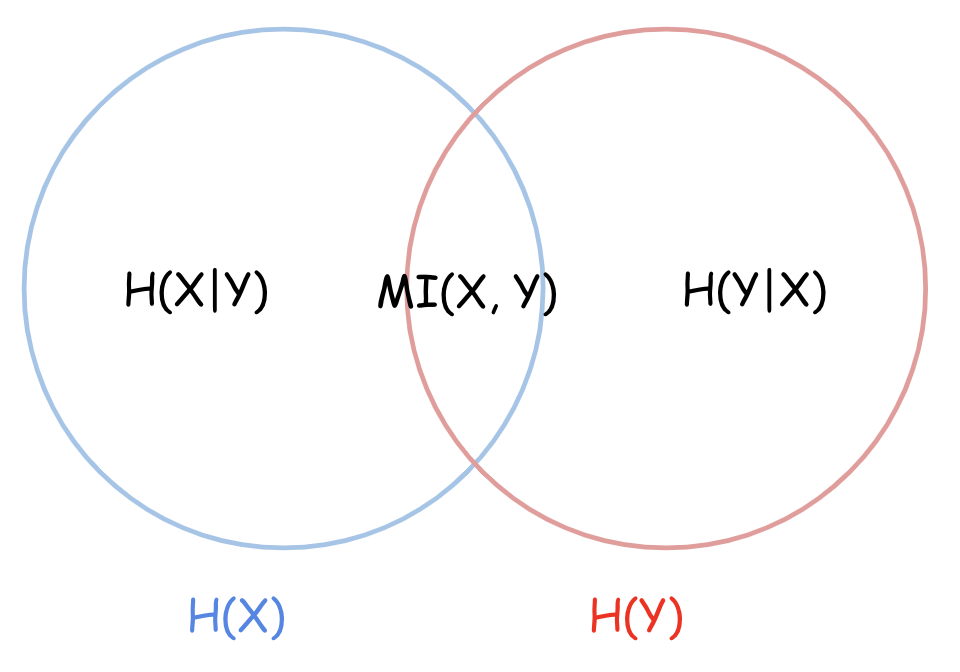
\begin{align} MI(X,Y) & = H(X) - H(X|Y) \tag{3.5.1} \\ & = H(Y) - H(Y|X) \tag{3.5.2} \\ & = H(X) + H(Y) - H(X,Y) \tag{3.5.3} \end{align}

　ここで、KL-divergenceと相互情報量 MI には以下の関係が成り立ちます。つまり、相互情報量 MI(X, Y) は、「確率変数 X と Y が独立でない場合の同時分布 P(X, Y)」と「独立である場合の同時分布 P(X)P(Y)」 の離れ具合（平均的な乖離度合い）を示しているのだと解釈できます。

\begin{align} MI(X, Y) & = D_{KL} \bigl( Pr(x, y) \mid\mid Pr(x)Pr(y) \bigr) \tag{3.6.1} \\ & = \mathbb{E}_{Y} \bigl[ D_{KL} \bigl( Pr(x|y) \mid\mid Pr(x) \bigr) \bigr] \tag{3.6.2} \\ & = \mathbb{E}_{X} \bigl[ D_{KL} \bigl( Pr(y|x) \mid\mid Pr(y) \bigr) \bigr] \tag{3.6.3} \\ \end{align}

（例）3.6.2の式展開

\begin{eqnarray} MI(X,Y) & = & \int \int Pr(x,y) \log \frac{Pr(x,y)}{Pr(x)Pr(y)} ~dxdy \\ & = & \int \int Pr(x|y)Pr(y) \log \frac{Pr(x|y)Pr(y)}{Pr(x)Pr(y)} ~dxdy \\ & = & \int Pr(y) \int Pr(x|y) \log \frac{Pr(x|y)}{Pr(x)} ~dx~dy \\ & = & \int Pr(y) \cdot D_{KL} \bigl( Pr(x|y) \mid\mid Pr(x) \bigr) ~dy \\ & = & \mathbb{E}_{Y} \bigl[ D_{KL} \bigl( Pr(x|y) \mid\mid Pr(x) \bigr) \bigr] \end{eqnarray}

2.2 KL-divergenceと対数尤度比

　ベイズ推定や統計モデリングでは、しばしば「真の分布 を、（パラメータの推定値 と確率モデル の組み合わせ）推定する」というモチベーションが起こります。そのため、２つの分布のズレを測りたいとき、あるいは推定誤差を損失関数やリスク関数に組み込んでパラメータに対する最適化問題をときたいときに、KL-divergenceを使います。

　KL-divergenceは最尤法をベースに、尤度比検定（Likelihood ratio test）、ベイズ因子（Bayse factor）、赤池情報量基準（AIC, Akaike's Information Critation）などのモデル選択手法*4と深い関わりを持ちます。

• 　真の分布 に対する推定分布 のKL-divergence： は次式のように、「 と の対数尤度比に対して、真の分布 で平均操作をおこなった値」です。

\begin{align} \left( 対数尤度比 \right) = \log \frac{q(x)}{p(x)} \tag{4} \end{align}

\begin{eqnarray} D_{KL}( Q \mid\mid P ) & := & \int q(x) \log \frac{q(x)}{p(x)} ~dx \\ & = & \mathbb{E}_{X} \left[ \log \frac{q(x)}{p(x)} \right] \left(: 平均対数尤度比 \right) \tag{5.1} \\ \end{eqnarray}

　　モデル比較・選択の評価値としてKL-divergenceを用いる場合、次式のように「KL-divergenceを最小にすること」と「平均対数尤度を最大にする」ことは等価になります。

\begin{eqnarray} D_{KL}( Q \mid\mid P ) & = & \mathbb{E}_{X} \bigl[ \log q(x) \bigr] - \mathbb{E}_{X} \bigl[ \log p(x) \bigr] \tag{5.2} \\ & \propto & - \mathbb{E}_{X} \bigl[ \log p(x) \bigr] \left(: - 平均対数尤度 \right) \tag{5.3} \end{eqnarray}

• パラメトリックな確率モデル （例えば線形回帰モデル）を考えた場合、何らかの損失関数 に対して最適なパラメータ と、その推定値 に対して、確率モデルの誤差は以下のようにKL-divergenceで表現されます。（ただし、 を対数尤度関数とする。）

\begin{align} \left( 対数尤度比 \right) = \log \frac{f(x|\theta_{0})}{f(x|\hat{\theta})} \tag{6} \end{align}

\begin{eqnarray} \hat{\theta} & :=& \underset{\theta \in \Theta}{\rm argmin} ~ L(\theta) \tag{7} \\ \\ D_{KL}( \theta_{0} \mid\mid \hat{\theta} ) & := & \int f(x|\theta_{0}) \log \frac{f(x|\theta_{0})}{f(x|\hat{\theta})} ~dx \\ & = & \mathbb{E}_{X} \left[ \log \frac{ f(x|\theta_{0}) }{ f(x|\hat{\theta}) } \right] \tag{8.1} \\ & = & \mathbb{E}_{X} \bigl[ \ell( \theta_{0}|x ) \bigr] - \mathbb{E}_{X} \bigl[ \ell( \hat{\theta}|x ) \bigr] \tag{8.2} \end{eqnarray}

2.3 KL-divergenceとFisher情報量

　確率モデル を仮定したとき、パラメータ のFisher情報量 は以下のように定義されます。（ただし、 を対数尤度関数とする。）

\begin{eqnarray} I(\theta) & := & \mathbb{E}_{X} \left[ { \left\{ \frac{d}{dx}\ell(\theta | x) \right\} }^{2} \right] \tag{9.1} \\ & = & \mathbb{E}_{X} \left[ { \left\{ \frac{d}{dx}\log f(x|\theta) \right\} }^{2} \right] \tag{9.2} \end{eqnarray}

　 　確率モデル を仮定したとき、KL-divergenceとFisher情報量 の間には、次のような関係*5が成り立ちます。

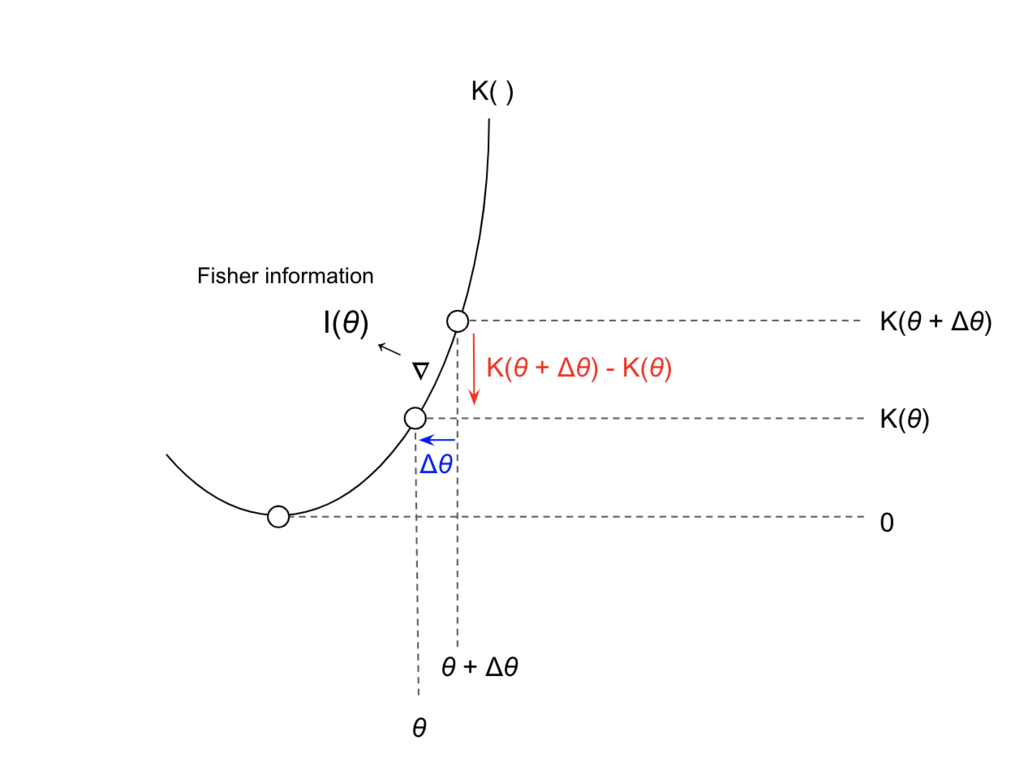
\begin{eqnarray} \lim_{h \to 0} \frac{1}{h^{2}} D_{KL} \bigl( f(x|\theta) \mid\mid f(x|\theta+h) \bigr) = \frac{1}{2} I(\theta) \tag{10} \end{eqnarray}

　この式は、 の近傍でのKL-divergence： は、 における確率モデル のFisher情報量 に比例することを示しています。つまり、Fisher情報量 は確率モデル が の近傍でもつ局所的な情報量を表していることがわかります。

つまり，パラメトリックな確率モデルに対するKL-divergenceの微小変化はFisher情報行列を計量行列として計算できます．

\begin{eqnarray} D_{KL}(p_{\theta}, p_{\theta + \Delta \theta}) &= \int p(x|\theta) \log \frac{p(x|\theta)}{p(x|\theta+\Delta \theta)} dx \ &\approx \frac{1}{2} {\Delta \theta}^T I(\theta) \Delta \theta \end{eqnarray}

3. 参考書籍

新装改訂版 現代数理統計学

現代数理統計学の基礎 (共立講座 数学の魅力)

数理統計学 (数学シリーズ)

Elements of Information Theory (Wiley Series in Telecommunications and Signal Processing)

情報量規準 (シリーズ・予測と発見の科学)

*1:一般化するとf-divergenceというクラスが定義できます。汎関数微分などの関数解析の知識が必要。。

*2:pythonのライブラリ関数scipy.stats.entropyを使いました。

*3:熱力学的なエントロピーはボルツマン発祥ですが、シャノンの情報量に関する歴史的背景については以下で言及されています。ハートレー→ナイキスト→シャノンという流れがあるみたい。http://www.ieice.org/jpn/books/kaishikiji/200112/200112-9.html

*4:情報量規準についての文献→ https://www.ism.ac.jp/editsec/toukei/pdf/47-2-375.pdf

*5:この式は、KL-divergenceをテイラー展開して二次形式で近似すると導出されます。$$ \ell(\theta + h) - \ell(\theta) = {\ell}^{'}(\theta)h + \frac{1}{2} {\ell}^{''}(\theta) h^{2} + O(h^{3}) $$

最尤推定・MAP推定・ベイズ推定を比較する

1. 推定のモチベーション

　確率変数 の真の分布 に対して、

$$ \begin{cases} 確率モデル　 ：　p(X|w) \\ 事前分布　　 ：　\varphi(w) \end{cases} $$

を仮定したとき、

$$ データサンプル 　　：　X^{n} := \left\{ X_1, \dots ,X_n \right\} $$

を用いて、 を推定したい。

2. 最尤推定（ML）

2.1 パラメータ の対数尤度

ベイズの定理： $$ \begin{eqnarray} p(w | X^{n}) = \frac{ p(X^{n}|w) \varphi(w) }{ \int_{W} p(X^{n}|w) \varphi(w) dw} \end{eqnarray} $$

において、以下で定義される対数尤度 は、手元にあるサンプルデータ に対する 、確率モデル の尤もらしさを示します。対数尤度 の示す値は、サンプルデータ がもつ"ばらつき"が加味されておらず、手元にあるデータの値に大きく依存するということに注意してください。

$$ \begin{eqnarray} \ell(w | \cdot) & := & \log p(\cdot | w) \\ \\ \ell(w | X^{n}) & := & \log p(X^{n} | w) \\ & = & \log \prod_{i=1}^{n} p(X_i | w) \end{eqnarray} $$

2.2 パラメータの推定（最尤推定量）

　最尤推定では、対数尤度 が最大となるようなパラメータ を選び、これを確率モデル におけるパラメータ の推定量とします。推定量 を最尤推定量と呼びます。

$$ \begin{eqnarray} \hat{w}_{ML} := \underset{w \in W}{\rm argmax} ~ \ell(w|X^{n}) \end{eqnarray} $$

以上から、最尤推定では、確率変数 の真の分布 は、サンプルデータ から求めた最尤推定量 と確率モデル によって次式のように推定されます。

$$ \begin{eqnarray} q(X) \approx p( X | \hat{w}_{ML} ) \end{eqnarray} $$

3. 事後確率最大化推定（MAP）

3.1 パラメータ の事後確率

ベイズの定理：

$$ \begin{eqnarray} p(w | X^{n}) = \frac{ p(X^{n}|w) \varphi(w) }{ \int_{W} p(X^{n}|w) \varphi(w) dw} \end{eqnarray} $$

において、以下で定義される事後確率 は、手元にあるサンプルデータ に対する 、確率モデル ・事前分布 の尤もらしさを示します。事後確率 の示す値は、サンプルデータ がもつ"ばらつき"が加味されておらず、その値に大きく依存するということに注意してください。

$$ \begin{eqnarray} p(w | \cdot) & := & \frac{1}{Z} \log p(\cdot | w)\varphi(w) \\ \\ p(w | X^{n}) & := & \frac{1}{Z_n} \log p(X^{n} | w)\varphi(w) \\ & = & \frac{1}{Z_n} \log \prod_{i=1}^{n} p(X_i | w)\varphi(w) \end{eqnarray} $$

• ただし、 は、それぞれベイズの定理における右辺の分子に対して で積分した値（正規化定数）を表す。

3.2 パラメータの推定（MAP推定量）

　MAP推定では、事後確率が最大となるようなパラメータ を選び、これを確率モデル におけるパラメータ の推定量とします。推定量 をMAP推定量と呼びます。

$$ \begin{eqnarray} \hat{w}_{MAP} := \underset{w \in W}{\rm argmax} ~ p(w|X^{n}) \end{eqnarray} $$

　以上から、MAP推定では、確率変数 の真の分布 は、サンプルデータ から求めたMAP推定量 と確率モデル によって次式のように推定されます。
$$ \begin{eqnarray} q(X) \approx p( X | \hat{w}_{MAP} ) \end{eqnarray} $$

4. ベイズ推定（Bayse）

4.1 パラメータ の平均対数尤度

ベイズの定理： $$ \begin{eqnarray} p(w | X^{n}) = \frac{ p(X^{n}|w) \varphi(w) }{ \int_{W} p(X^{n}|w) \varphi(w) dw} \end{eqnarray} $$

において、以下で定義される平均対数尤度 は、 に対して期待値をとった（ のばらつきによる偶然誤差を排除した）上での、確率モデル の尤もらしさを示します。

$$ \begin{eqnarray} K(w) & := & \mathbb{E}_{X} \left[ \log p(X | w) \right] \tag{期待対数尤度} \\ \\ K_n(w) & := & \frac{1}{n} \sum_{i=1}^{n} \log p(X_i | w) \tag{経験対数尤度} \end{eqnarray} $$

パラメータの推定量を求めるため、平均対数尤度を符号反転したものを、損失関数 として定義します。

$$ \begin{eqnarray} L(w) & := & - K(w) = \mathbb{E}_{X} \left[ - \log p(X | w) \right] \tag{期待損失関数} \\ \\ L_n(w) & := & - K_{n}(w) = \frac{1}{n} \sum_{i=1}^{n} \left\{ - \log p(X_i | w) \tag{経験損失関数} \right\} \end{eqnarray} $$

4.2 確率分布 の推定（予測分布）

　ベイズ推定では、損失関数が最小となるようなパラメータ を選び、これを確率モデル と事前分布 によって求められる事後分布 の平均値の推定量とみなします。ここで、最尤推定やMAP推定では、「確率モデル に対して与えるパラメータ はある1つの値に決まる」と仮定していますが、ベイズ推定では「パラメータ は事前分布 によって確率的に変動する値（=確率変数）である」と仮定していることに注意します。推定量 をベイズ推定量*1と呼びます。

$$ \begin{eqnarray} \hat{w}_{0} := \underset{w \in W}{\rm argmax} ~ L_{n}(w) \end{eqnarray} $$

　推定量 は「事後分布において がとり得ると期待される（尤もらしい）値」と考えられます。しかし、ベイズ推定において、確率変数 の真の分布 を、 によって推定することはしません。その代わり、推定量 を平均にもつ事後分布 から求められる予測分布 を用いて真の分布 を推定します。

$$ \begin{eqnarray} q(X) \approx p^{*}(X) & := & \int_{W} p(X|w)p(w|X^{n}) dw \end{eqnarray} $$

　上図は、確率モデル・事前分布・事後分布がすべて正規分布に従う場合の各分布を表す。Prior（事前分布）の「ばらつき」に対して、Likelihood（尤度, 最尤推定で用いる）と Posterior（事後分布, MAP推定で用いる）は、より小さい「ばらつき」をもつ。

5. 参考図書

StanとRでベイズ統計モデリング (Wonderful R)

データ解析のための統計モデリング入門――一般化線形モデル・階層ベイズモデル・MCMC (確率と情報の科学)

ベイズ統計の理論と方法

*1:他の言い方もあるようです。