scikit-learn : pythonで重回帰分析をやってみた

f:id:yumaloop:20180425131518p:plain:w600 — multiple-regression

1. 重回帰分析についての所感
2. scikit-learnのサンプルデータセットで重回帰分析を試してみる
3. プログラム - Python3.x系
4. 参考文献

1. 重回帰分析についての所感

1.1. 用語など

英語だと, Multiple Regression.
変数の呼び方は色々ある．
{説明変数or予測変数or独立変数} vs {被説明変数or応答変数or目的変数}
いわゆる一般化線形モデル群(GLM)の一角．単回帰/重回帰/多項式回帰は線形モデル(LM)だが，ロジスティック回帰は狭義の線形モデル(LM)ではない．
"線形(Linear)"という語は，「説明変数→目的変数」ではなく「説明変数の係数(パラメータ)→目的変数」という写像の性質を指している．
説明変数どうしの関係に対して，モデルは固定効果 or 変量効果を仮定する．両方の効果を仮定するものは「混合モデル」と呼ばれる．
誤差項が「正規分布に従う」と仮定するモデルは「一般線形モデル」，誤差が「任意の分布に従う」と仮定するモデルは，「一般化線形モデル」という．

1.2. モデル評価：「モデル」の性能を学習結果から評価する

決定係数R^2の他にも、MAE(平均絶対誤差), MSE(平均二乗誤差)など色々ある．だいたい似たような結果になる．詳細はこちら．
自由度調整済みR^2は, scikit-learnにないらしく，自分で定義する必要あり.
「帰無仮説 : 偏回帰係数が0」でn元配置分散分析(F検定)をするのが通説．scikit-learn だと簡単にできない(?)．
R^2・MAE・MSEの値や仮説検定の結果に加えて、残差分析(プロット)などの可視化による検証が有効.

1.3. モデル選択：「モデルの適用」に対する妥当性を検証する

「外れ値」はないか？→欠損処理
「系列相関」はないか？→ダービン・ワトソン検定
「データが独立同分布からなる」という仮定は妥当か？→残差分析、残差プロット
「誤差項が独立同分布からなる」という仮定は妥当か？→残差分析、残差プロット
「誤差項は正規分布に従う」という仮定は妥当か？→F検定や信頼区間を見直し
「説明変数が互いに独立」という仮定は妥当か？→交互作用、多重線形性の検証
「データに対する残差の等分散性」という仮定は妥当か？→重み付き2乗法
「変数選択」は妥当か？→自由度調整済みR^2、マローズのCp規準、AIC
「Overfit、予測能力、汎化能力」は妥当か？→AIC、WAIC、Cross validation
「尤もらしさ、データへの表現力」は妥当か？→BIC、Bayse factor

1.4. Pythonでの実装まわり

重回帰分析に関しては，pythonよりRの方が早い説．Rのglm()が超優秀.
もちろん，scikit-learn以外のモジュールを使う方法もある．例：statsmodels

blog.datarobot.com

2. scikit-learnのサンプルデータセットで重回帰分析を試してみる

2.1. データ：skearn.datasets.load_boston

　　データセットはscikit-learnにあるサンプルデータ「ボストン市の地域情報」を使う．今回は，以下の9つの特徴量を使う．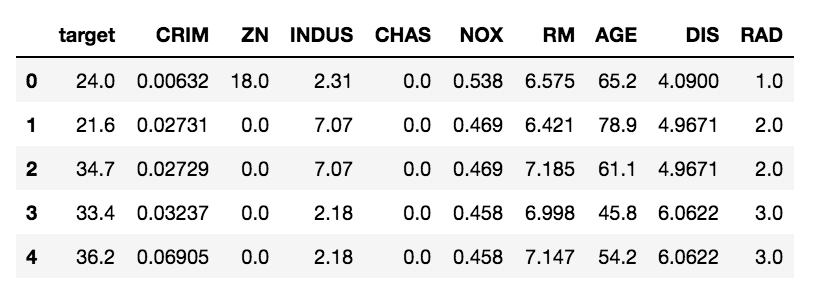
f:id:yumaloop:20190119155314p:plain:w600

target - 住宅価格

CRIM - 犯罪発生率

ZN - 住居区画の密集度

INDUS - 非小売業の土地割合

CHAS - チャールズ川 (1: 川の周辺, 0: それ以外)

NOX - NOx濃度

RM - 住居の平均部屋数

AGE - 1940年より前に建てられた物件割合

DIS - 5つのボストン市の雇用施設からの重み付き距離

RAD - 大きな道路へのアクセスしやすさ

　　データの散布図行列*1はこんな感じ(↓).
　　相関がありそうな説明変数のペアについては, 多重共線性を考えるべき.

f:id:yumaloop:20190119161256p:plain:w550

2.2. モデル：9次多項式でfitting

　　ボストン市の住宅価格targetを目的変数にして重回帰モデルを作る.
　　今回のモデルは，9次元空間から1次元空間への写像を9元多項式で表現したもの.
　　　※ 目的変数：target (1コ)
　　　※ 説明変数：CRIM, ZN, INDUS, CHAS, NOX, RM, AGE, DIS, RAD (9コ)
　　　※ 誤差項　：u (平均0, 正規分布に従う)

$y=\beta_0 + \beta_1 x_1 + \beta_2 x_2 + \dots + \beta_9 x_9 + u$

2.3. 前処理 : sklearn.model_selection.train_test_split

　　train-testの分割では一番簡単なホールド・アウト法を使う.
　　データの正規化や次元削減は省略した.

3. プログラム - Python3.x系

Pythonのスクリプトをかく.

import numpy as np
import pandas as pd
from sklearn.datasets import load_boston

# make data samples
boston = load_boston()
data   = pd.DataFrame(boston.data, columns = boston.feature_names)
target = pd.DataFrame(boston.target, columns = ['target'])

df = pd.concat([target, data], axis = 1)
df = df.iloc[:, :10]

# set x to explanatory variable 
# set y to response variable
x = df.iloc[:, 1:]
y = df.loc[:, ['target']]

# split data by Hold-out-method
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.3, random_state = 0)

# fitting train-data to the model
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(x_train, y_train)

# predicting y of test-data by the model
y_test_pred = lr.predict(x_test)

# estimated value of params
print('\n[Estimated values of the params]')
print('  Intercept    :', lr.intercept_)
print('  Coefficient  :', lr.coef_)

# model evaluation
from sklearn.metrics import mean_absolute_error, mean_squared_error
print('\n[Model evaluation]')
print('  R^2 on train               : %.5f' % lr.score(x_train, y_train))
print('  R^2 on test                : %.5f' % lr.score(x_test, y_test))
print('  MAE  (Mean-Absolute-Error) :',  mean_absolute_error(y_test, y_test_pred))
print('  MSE  (Mean-Squared-Error)  :',  mean_squared_error(y_test, y_test_pred))
print('  RMSE (Rooted-MSE)          :',  np.sqrt(mean_squared_error(y_test, y_test_pred)))

以上を実行すると, 次のような結果を得られる. Oh, that's the overfitting! :D

[Estimated values of the params]
  Intercept    : [-1.83284178]
  Coefficient  : [ [-0.18424554  0.06424141 -0.22994428  4.17534912 -8.45210943  6.93761463
  -0.06944658 -1.81172533 -0.07995724] ]

[Model evaluation]
  R^2 on train               : 0.66568
  R^2 on test                : 0.54068
  MAE  (Mean-Absolute-Error) : 4.133489445028324
  MSE  (Mean-Squared-Error)  : 38.245841746617565
  RMSE (Rooted-MSE)          : 6.184322254428335

回帰問題でよく使う評価指標については，下記の記事にまとめたので，よければどうぞ．
yul.hatenablog.com