閃き- blog

きらびやかに、美しく、痛烈に．

正則行列と正規行列（ムーア・ペンローズ逆行列, エルミート行列, ユニタリー行列）

数学備忘

N×Nの正方行列： ${\bf A}=\left( \begin{array}{cccc} a_{11} & a_{12} & \ldots & a_{1N} \\ a_{21} & a_{22} & \ldots & a_{2N} \\ \vdots & \vdots & \ddots & \vdots \\ a_{N1} & a_{N2} & \ldots & a_{NN} \end{array} \right)$ について考える。

1. 正則行列

以下の命題は同値である。

※ $f_{A}({\bf x})={\bf Ax}$ を満たす写像 $f_{A}:{{\mathbb{R}}^{N}}~{\to}~{{\mathbb{R}}^{N}}$ を、 $\mathrm{N}$ 次行列 ${\bf A}$ に対応する1次変換とする。

行列 ${\bf A}$ は正則行列である。

行列 ${\bf A}$ に対して、 ${\bf A}{\bf A^{-1}}~=~{\bf I}$ を満たす逆行列 ${\bf A^{-1}}$ が存在する

行列 ${\bf A}$ に対して、行列式 $|{\bf A}|~{\neq}~0$ である。

行列 ${\bf A}$ に対して、 $rank({\bf A})~=~{\mathrm{N}}$ である。

行列 ${\bf A}$ に対して、すべての固有値が $0$ ではない。

行列 ${\bf A}$ に対して、連立1次方程式「 ${\bf Ax}={\bf b}$ 」が唯一解をもつ。

行列 ${\bf A}$ に対して、連立1次方程式「 ${\bf Ax}={\bf 0}$ 」の解は ${\bf x}~=~{\bf 0}$ のみ。

行列 ${\bf A}$ に対して、 ${\bf A}$ の列ベクトル $({\bf a_{1}},~{\bf a_{2}},~{\cdots},~{\bf a_{N}})$ は一次独立。

行列 ${\bf A}$ に対して、 $f_{A}$ は「全単射」である。

行列 ${\bf A}$ に対して、 $f_{A}$ は $Imf_{A}={\mathbb{R}}^{N}$ をみたす。

行列 ${\bf A}$ に対して、 $f_{A}$ は $Kerf_{A}=\{ {\bf 0} \}$ をみたす。

2. ムーア・ペンローズ 逆行列

以下の性質（１）〜（４）を満たす行列 ${\bf A^{+}}$ を、「行列 $\bf A$ に対するムーア・ペンローズ逆行列」という。

（１） ${\bf A}{\bf A^{+}}{\bf A}~=~{\bf A}$

（２） ${\bf A^{+}}{\bf A}{\bf A^{+}}~=~{\bf A^{+}}$

（３） ${({{\bf A^{+}}{\bf A}})}^{\mathrm{T}}~=~{\bf A^{+}}{\bf A}$

（４） ${({{\bf A}{\bf A^{+}}})}^{\mathrm{T}}~=~{\bf A}{\bf A^{+}}$

ある行列 $\bf A$ に対して、（１）を満たす行列 $\bf A^{+}$ は複数あり、これを「一般逆行列」という。
ある行列 $\bf A$ に対して、（１）〜（４）を満たす行列 $\bf A^{+}$ はただ１つに定まり、これを「ムーア・ペンローズ逆行列」という。

また、 ${{\bf A^{+}}{\bf A}}$ と ${{\bf A}{\bf A^{+}}}$ はエルミート行列である。

3. 正規行列

以下の命題は同値である。

行列 ${\bf A}$ は正規行列である。

行列 ${\bf A}$ に対して、 ${\bf A^{\mathrm{*}}}{\bf A}={\bf A}{\bf A^{\mathrm{*}}}$ が成り立つ。

行列 ${\bf A}$ に対して、 ${\bf A}$ は対角化可能である。

※ 随伴行列 ${\bf A}^{*}$

一般に、行列 ${\bf A}$ の随伴行列 ${\bf A}^{*}$ は、 ${\bf A}$ の「転置行列」を各成分において「複素共軛（実部はそのままで虚部の符号を反転する）」したものとして定義される。

なお、 ${\bf A}$ が複素行列である場合、以下の等式が成り立つ。

　　　 ${\bf A}^{*}=\overline{{\bf A}^{-1}}$

さらに、 ${\bf A}$ が実行列である場合、以下の等式が成り立つ。

　　　 ${\bf A}^{*}={\bf A}^{-1}$

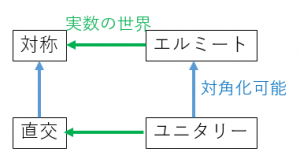
4. エルミート行列とユニタリー行列（複素行列への拡張）

N×Nの複素正方行列： ${\bf A}$ に対して、以下の呼び名が定義される。

行列 ${\bf A}$ が「対称行列」である。　　　 $~{\Leftrightarrow}~~~{\bf A}={\bf A^{\mathrm{T}}}$
行列 ${\bf A}$ が「直交行列」である。　　　 $~{\Leftrightarrow}~~~{\bf A}{\bf A^{\mathrm{T}}}={\bf I}$
行列 ${\bf A}$ が「エルミート行列」である。 $~{\Leftrightarrow}~~~{\bf A}={\bf A^{\mathrm{*}}}$
行列 ${\bf A}$ が「ユニタリー行列」である。 $~{\Leftrightarrow}~~~{\bf A}{\bf A^{\mathrm{*}}}={\bf I}$

ここで、「対称行列」「直交行列」「エルミート行列」「ユニタリー行列」はいずれも正規行列であり、対角化可能となる。
エルミート行列は、対称位置にある成分が互いに複素共役になっている。

5. まとめ

◯「逆行列」　　(→正方行列である前提を拡張すると...)　「ムーア・ペンローズ逆行列」

◯「対称行列」　(→実行列である前提を拡張すると...)　　「エルミート行列」
　
◯「直交行列」　(→実行列である前提を拡張すると...)　　「ユニタリー行列」

参考：

随伴行列 - Wikipedia