Kullback-Leibler Divergenceについてまとめる

1. KL-divergenceとは?
2. 諸量との関係
3. 参考書籍

!! お知らせ（2020.06.10） * こちらの記事の英語版を公開しました．よければご覧ください．
Here is the english translation of this post. Please check it if you want.

1. KL-divergenceとは?

　統計学や情報理論をはじめとした広い分野で、KL-divergence*1はたびたび登場します。KL-divergenceは、「尤度比（尤もらしさを比較する尺度）を log 変換し（乗算操作を線形結合に直す、凸関数だから最適化との相性良い）、期待値（確率密度の重み付きの積分、ルベーグ積分）をとったもの」として定義されます。

1.1 定義

　一般に、確率分布 $P, ~ Q$ が確率密度関数 $p(x), ~ q(x)$ をもつとき、KL-divergence（Kullback-Leibler divergence）は、以下のように定義されます。

\begin{eqnarray} D_{KL}( Q \mid\mid P ) := \int q(x) \log \frac{q(x)}{p(x)} ~dx \tag{1} \end{eqnarray}

1.2 基本的な性質

　KL-divergenceは以下のような性質をもちます。

（非負性）非負の値域をもつ。

\begin{align} 0 \leq D_{KL}( Q \mid\mid P ) \leq \infty \tag{2.1} \end{align}

（完備性）値が 0 のとき、2つの確率分布 P と Q は同等。

\begin{align} D_{KL}( Q \mid\mid P ) = 0 ~~ \Leftrightarrow ~~ P = Q \tag{2.2} \end{align}

（非対称性）値は P と Q に対して対称性を持たない。

\begin{align} D_{KL}( Q \mid\mid P ) \neq D_{KL}( P \mid\mid Q ) \tag{2.3} \end{align}

（絶対連続性）値が発散しない限り、Q は P に関して絶対連続である。

\begin{align} D_{KL}( Q \mid\mid P ) \lt \infty ~~ \Rightarrow ~~ P \gg Q \tag{2.4} \end{align}

　例として、2つの正規分布間でKL-divergenceを計算*2すると、以下のような値になります。分布のズレが大きくなるほど、値が増加していることがわかります。

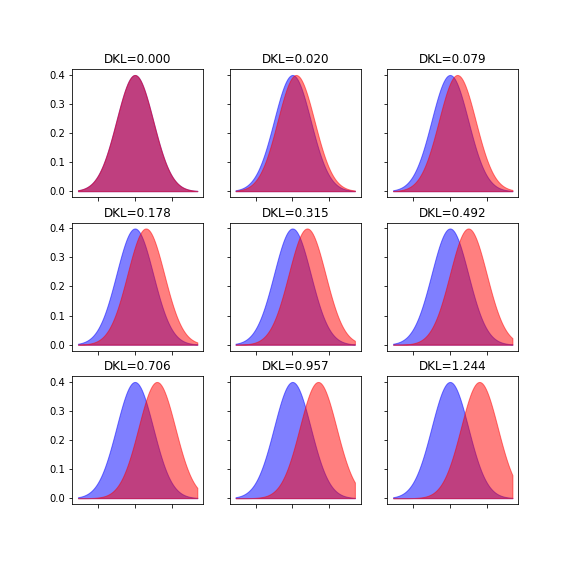
f:id:yumaloop:20190109162028p:plain:w500

1.3 KL-divergenceは距離なのか？

　KL-divergenceは、確率や情報を考える際にとても重要な量であるため、分野や文脈によって様々な名称で呼ばれます。

"KL-divergence"
"KL-metrics"
"KL-information"
"Information divergence"
"Information gain"
"Relative entropy"

　KL-divergenceはつねに非負の値をとるため、これは確率分布 P と Q が存在する空間における距離(metrics)を示していると解釈することができます。しかし、KL-divergenceは次の距離の公理のうち「非負性」と「完備性」しか満たさないため、厳密には距離(metrics) ではありません。

距離 $d(~)$ の公理

非負性　　　　 $d(x, ~ y) \geq 0$

完備性　　　　 $d(x, ~ y) = 0 ~~ \Leftrightarrow ~~ x = y$

対称性　　　　 $d(x, ~ y) = d(y, ~ x)$

三角不等式　　 $d(x, ~ y) + d(y, ~ z) \geq d(x, ~ z)$

　例えば、ユークリッド距離、二乗距離、マハラビノス距離、ハミング距離などは、この4つの条件をすべて満たすため、明らかに距離(metrics)として扱うことができます。一方で、KL-divergenceは距離(metrics)ではなくdivergenceです。"divergence"とは、距離の公理における４つの条件のうち「非負性」「対称性」のみを採用したものであり、"距離(metrics)"の拡張概念です。距離の公理による制約を減らし、抽象度の高い議論をしようというわけです。

　なお、このdivergenceという語は発散と訳されることが一般的で、例えば物理学ではベクトル作用素 div として登場します。divergenceのイメージに該当する日本語はありませんが、相違度、分離度、逸脱度、乖離度などが使われているようです。

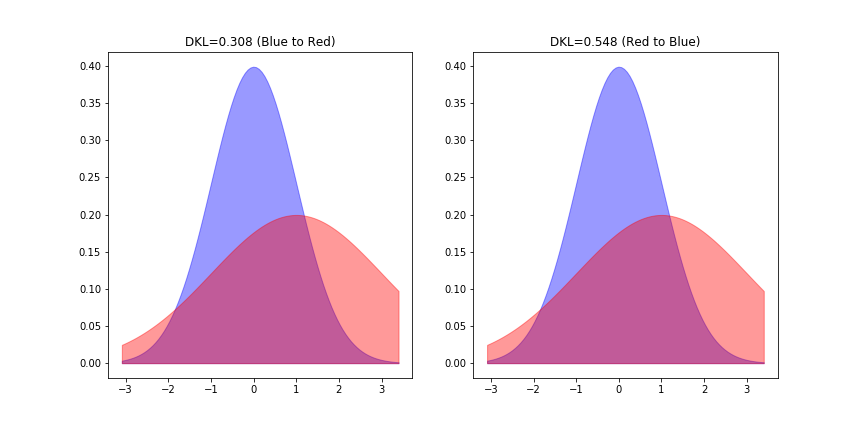
　実例として、2つの正規分布 $N(0, 1)$ （青）と $N(1, 2)$ （赤）の間のKL-divergenceを測ってみましょう。左が青からみた赤とのKL距離、右が赤からみた青とのKL距離となっており値が異なることがわかります。なお「等分散正規分布間のKL-divergence」という特殊な条件下では、対称性が成り立ちます。

また，確率分布間の近さを測る尺度としては，KL情報量の他にも次のようなものが知られています．

確率分布 $q(x), p(x)$ 間の"距離"を測る量

${\chi}^2(q ; p) := \sum_{i=1}^{k} {\large \frac{{(p_i - q_i)}^2}{p_i} }$ 　　　　　　　　 ${\chi}^2$ 統計量

$L_1(q ; p) := \int | q(x) - p(x) | ~ dx$ 　　　　　　 $L_1$ -ノルム

$L_2(q ; p) := \int { \{ q(x) - p(x) \} }^{2} ~ dx$ 　　　　　 $L_2$ -ノルム

$I_K(q ; p) := \int { \{ \sqrt{ q(x) } - \sqrt{ p(x) } \} }^{2} ~ dx$ 　　ヘリンジャー距離

$\mathbb{D}(q ; p) := \int f \left( {\large \frac{q(x)}{p(x)} } \right) q(x) ~ dx$ 　　　　　　 $f$ -ダイバージェンス　

$I_{\lambda}(q ; p) := \int \left\{ { \left( {\large \frac{q(x)}{p(x)} } \right) }^{\lambda} - 1 \right\} q(x) ~ dx$ 　　一般化情報量(Kawada, 1987)

$\mathbb{D}_{KL}(q ; p) := \int \log \left( {\large \frac{q(x)}{p(x)} } \right) q(x) ~ dx$ 　　　　 KL情報量

2. 諸量との関係

2.1 KL-divergenceと相互情報量

　エントロピー $H(X)$ 、結合エントロピー $H(X,Y)$ 、条件つきエントロピー $H(X|Y)$ 、相互情報量 $MI(X,Y)$ は、確率密度 $Pr(~)$ を用いて以下のように定義されます。*3

\begin{align} H(X) & := - \int Pr(x) \log Pr(x) ~dx \tag{3.1} \\ H(X,Y) & := - \int Pr(x,y) \log Pr(x,y) ~dy~dx \tag{3.2} \\ H(X|Y) & := - \int Pr(x,y) \log Pr(x|y) ~dx~dy \tag{3.3} \\ MI(X,Y) & := \int \int Pr(x,y) \log \frac{Pr(x,y)}{Pr(x)Pr(y)} ~dxdy \tag{3.4} \end{align}

2つの確率変数 X, Y について、相互情報量 MI（: Mutual Information）によって相互の関係性が明示されます。

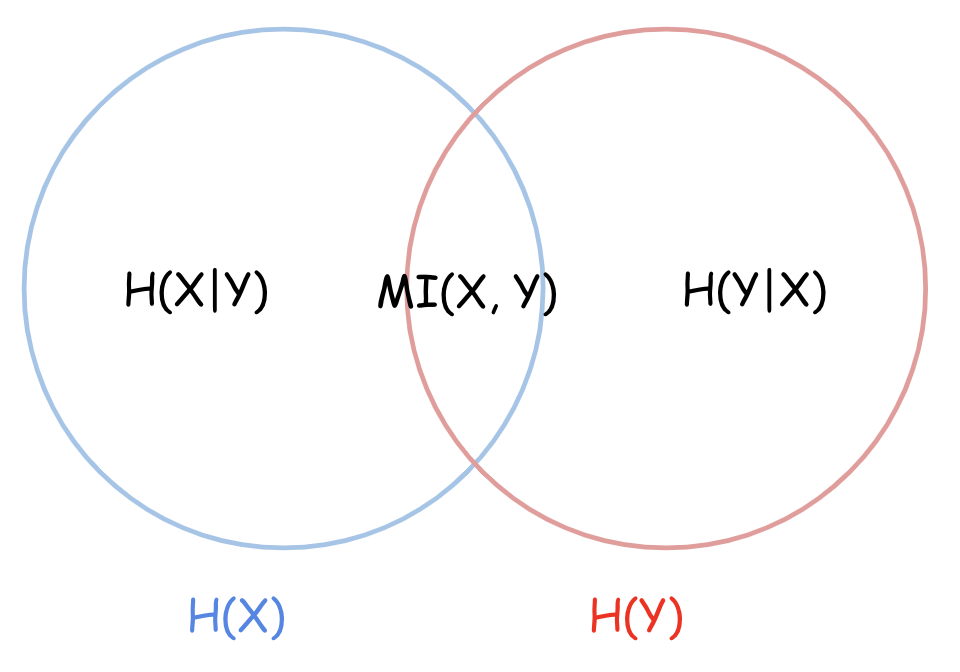
f:id:yumaloop:20190107163949p:plain:w400

\begin{align} MI(X,Y) & = H(X) - H(X|Y) \tag{3.5.1} \\ & = H(Y) - H(Y|X) \tag{3.5.2} \\ & = H(X) + H(Y) - H(X,Y) \tag{3.5.3} \end{align}

　ここで、KL-divergenceと相互情報量 MI には以下の関係が成り立ちます。つまり、相互情報量 MI(X, Y) は、「確率変数 X と Y が独立でない場合の同時分布 P(X, Y)」と「独立である場合の同時分布 P(X)P(Y)」の離れ具合（平均的な乖離度合い）を示しているのだと解釈できます。

\begin{align} MI(X, Y) & = D_{KL} \bigl( Pr(x, y) \mid\mid Pr(x)Pr(y) \bigr) \tag{3.6.1} \\ & = \mathbb{E}_{Y} \bigl[ D_{KL} \bigl( Pr(x|y) \mid\mid Pr(x) \bigr) \bigr] \tag{3.6.2} \\ & = \mathbb{E}_{X} \bigl[ D_{KL} \bigl( Pr(y|x) \mid\mid Pr(y) \bigr) \bigr] \tag{3.6.3} \\ \end{align}

（例）3.6.2の式展開

\begin{eqnarray} MI(X,Y) & = & \int \int Pr(x,y) \log \frac{Pr(x,y)}{Pr(x)Pr(y)} ~dxdy \\ & = & \int \int Pr(x|y)Pr(y) \log \frac{Pr(x|y)Pr(y)}{Pr(x)Pr(y)} ~dxdy \\ & = & \int Pr(y) \int Pr(x|y) \log \frac{Pr(x|y)}{Pr(x)} ~dx~dy \\ & = & \int Pr(y) \cdot D_{KL} \bigl( Pr(x|y) \mid\mid Pr(x) \bigr) ~dy \\ & = & \mathbb{E}_{Y} \bigl[ D_{KL} \bigl( Pr(x|y) \mid\mid Pr(x) \bigr) \bigr] \end{eqnarray}

2.2 KL-divergenceと対数尤度比

　ベイズ推定や統計モデリングでは、しばしば「真の分布 $q$ を、 $p(x|\hat{w})$ （パラメータの推定値 $\hat{w}$ と確率モデル $p(x|w)$ の組み合わせ）推定する」というモチベーションが起こります。そのため、２つの分布のズレを測りたいとき、あるいは推定誤差を損失関数やリスク関数に組み込んでパラメータに対する最適化問題をときたいときに、KL-divergenceを使います。

　KL-divergenceは最尤法をベースに、尤度比検定（Likelihood ratio test）、ベイズ因子（Bayse factor）、赤池情報量基準（AIC, Akaike's Information Critation）などのモデル選択手法*4と深い関わりを持ちます。

　真の分布 $P$ に対する推定分布 $p$ のKL-divergence： $D_{KL}(Q \mid\mid P)$ は次式のように、「 $q$ と $p$ の対数尤度比に対して、真の分布 $q$ で平均操作をおこなった値」です。

\begin{align} \left( 対数尤度比 \right) = \log \frac{q(x)}{p(x)} \tag{4} \end{align}

\begin{eqnarray} D_{KL}( Q \mid\mid P ) & := & \int q(x) \log \frac{q(x)}{p(x)} ~dx \\ & = & \mathbb{E}_{X} \left[ \log \frac{q(x)}{p(x)} \right] \left(: 平均対数尤度比 \right) \tag{5.1} \\ \end{eqnarray}

　　モデル比較・選択の評価値としてKL-divergenceを用いる場合、次式のように「KL-divergenceを最小にすること」と「平均対数尤度を最大にする」ことは等価になります。

\begin{eqnarray} D_{KL}( Q \mid\mid P ) & = & \mathbb{E}_{X} \bigl[ \log q(x) \bigr] - \mathbb{E}_{X} \bigl[ \log p(x) \bigr] \tag{5.2} \\ & \propto & - \mathbb{E}_{X} \bigl[ \log p(x) \bigr] \left(: - 平均対数尤度 \right) \tag{5.3} \end{eqnarray}

パラメトリックな確率モデル $f(x|\theta)$ （例えば線形回帰モデル）を考えた場合、何らかの損失関数 $L$ に対して最適なパラメータ $\theta_{0}$ と、その推定値 $\hat{\theta}$ に対して、確率モデルの誤差は以下のようにKL-divergenceで表現されます。（ただし、 $\ell( \cdot| x )$ を対数尤度関数とする。）

\begin{align} \left( 対数尤度比 \right) = \log \frac{f(x|\theta_{0})}{f(x|\hat{\theta})} \tag{6} \end{align}

\begin{eqnarray} \hat{\theta} & :=& \underset{\theta \in \Theta}{\rm argmin} ~ L(\theta) \tag{7} \\ \\ D_{KL}( \theta_{0} \mid\mid \hat{\theta} ) & := & \int f(x|\theta_{0}) \log \frac{f(x|\theta_{0})}{f(x|\hat{\theta})} ~dx \\ & = & \mathbb{E}_{X} \left[ \log \frac{ f(x|\theta_{0}) }{ f(x|\hat{\theta}) } \right] \tag{8.1} \\ & = & \mathbb{E}_{X} \bigl[ \ell( \theta_{0}|x ) \bigr] - \mathbb{E}_{X} \bigl[ \ell( \hat{\theta}|x ) \bigr] \tag{8.2} \end{eqnarray}

2.3 KL-divergenceとFisher情報量

　確率モデル $f(\cdot | \theta)$ を仮定したとき、パラメータ $\theta$ のFisher情報量 $I(\theta)$ は以下のように定義されます。（ただし、 $\ell( \cdot | x )$ を対数尤度関数とする。）

\begin{eqnarray} I(\theta) & := & \mathbb{E}_{X} \left[ { \left\{ \frac{d}{dx}\ell(\theta | x) \right\} }^{2} \right] \tag{9.1} \\ & = & \mathbb{E}_{X} \left[ { \left\{ \frac{d}{dx}\log f(x|\theta) \right\} }^{2} \right] \tag{9.2} \end{eqnarray}

　　確率モデル $f(\cdot | \theta)$ を仮定したとき、KL-divergenceとFisher情報量 $I(\theta)$ の間には、次のような関係*5が成り立ちます。

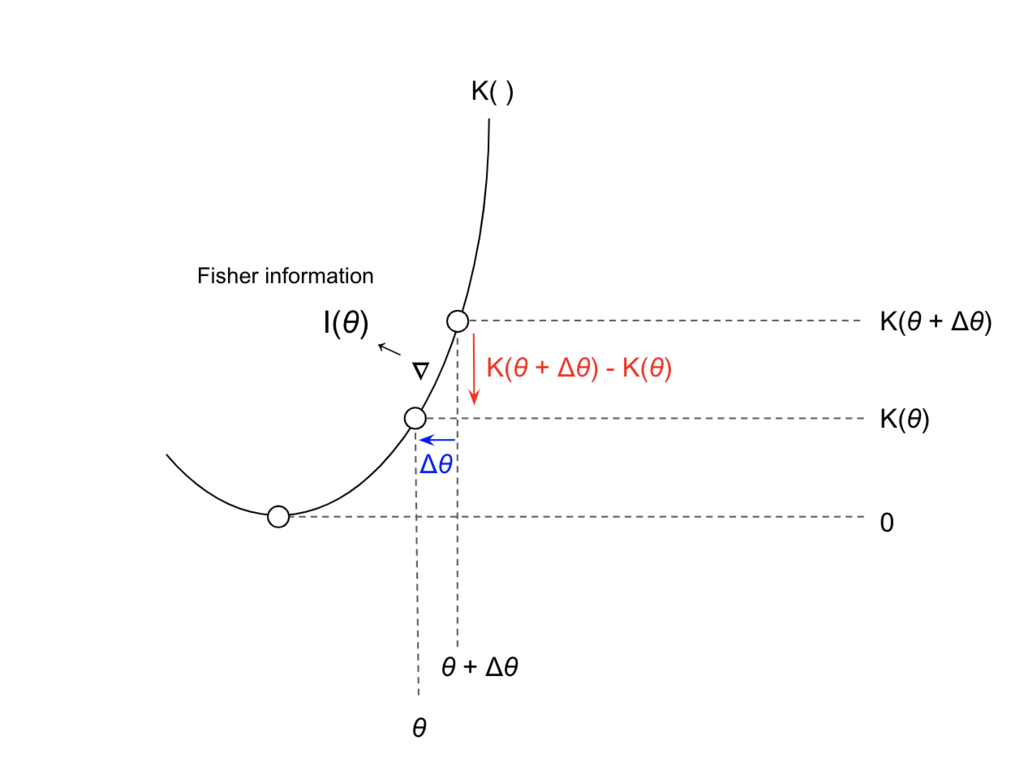
\begin{eqnarray} \lim_{h \to 0} \frac{1}{h^{2}} D_{KL} \bigl( f(x|\theta) \mid\mid f(x|\theta+h) \bigr) = \frac{1}{2} I(\theta) \tag{10} \end{eqnarray}

　この式は、 $\theta$ の近傍でのKL-divergence： $D_{KL} \bigl( f(x|\theta) \mid\mid f(x|\theta+h) \bigr)$ は、 $\theta$ における確率モデル $f(\cdot|\theta)$ のFisher情報量 $I(\theta)$ に比例することを示しています。つまり、Fisher情報量 $I(\theta)$ は確率モデル $f(\cdot | \theta)$ が $\theta$ の近傍でもつ局所的な情報量を表していることがわかります。

つまり，パラメトリックな確率モデル $p(x \vert \theta)$ に対するKL-divergenceの微小変化はFisher情報行列 $I(\theta)$ を計量行列として計算できます．

\begin{eqnarray} D_{KL}(p_{\theta}, p_{\theta + \Delta \theta}) &= \int p(x|\theta) \log \frac{p(x|\theta)}{p(x|\theta+\Delta \theta)} dx \ &\approx \frac{1}{2} {\Delta \theta}^T I(\theta) \Delta \theta \end{eqnarray}

f:id:yumaloop:20190107190651p:plain:w600

3. 参考書籍

新装改訂版現代数理統計学

作者:彰通, 竹村
発売日: 2020/11/10
メディア: 単行本

現代数理統計学の基礎 (共立講座数学の魅力)

作者:達也, 久保川
発売日: 2017/04/07
メディア: 単行本

数理統計学 (数学シリーズ)

作者:宣生, 稲垣
発売日: 2003/02/25
メディア: 単行本

Elements of Information Theory (Wiley Series in Telecommunications and Signal Processing)

作者:Cover, Thomas M.,Thomas, Joy A.
発売日: 2006/06/30
メディア: ハードカバー

情報量規準 (シリーズ・予測と発見の科学)

作者:貞則, 小西,源四郎, 北川
発売日: 2004/09/01
メディア: 単行本

*1:一般化するとf-divergenceというクラスが定義できます。汎関数微分などの関数解析の知識が必要。。

*2:pythonのライブラリ関数scipy.stats.entropyを使いました。

*3:熱力学的なエントロピーはボルツマン発祥ですが、シャノンの情報量に関する歴史的背景については以下で言及されています。ハートレー→ナイキスト→シャノンという流れがあるみたい。http://www.ieice.org/jpn/books/kaishikiji/200112/200112-9.html

*4:情報量規準についての文献→ https://www.ism.ac.jp/editsec/toukei/pdf/47-2-375.pdf

*5:この式は、KL-divergenceをテイラー展開して二次形式で近似すると導出されます。$$ \ell(\theta + h) - \ell(\theta) = {\ell}^{'}(\theta)h + \frac{1}{2} {\ell}^{''}(\theta) h^{2} + O(h^{3}) $$