Simon Wood先生の"lockdown reading list"

加法モデルのテキストで有名なイギリスの統計学者Simon Wood先生が，自身のホームページ上で，"the lockdown reading list"なるものを紹介していたので紹介します．（ほとんどがBlackwellの本です）

• Collapse (Jared Diamond) on how societies are destroyed, not by external forces, but by their failure to adapt their cultural norms to those forces.
• Thinking Fast and Slow (Daniel Kahneman) on the pitfalls of our intuitive reasoning, especially about risk and uncertainty.
• Mistakes were made, but not by me (Carol Tarvis and Elliot Aronson) on the psychology of sticking with bad decisions.
• The Parable of the Old Man and the Young by Wilfred Owen, on consequences of the above.
• Economics The User's Guide (Ha-Joon Chang) on what you really need to know about economics, and how it isn't just a scaled up version of household accounting.
• The Great Crash 1929 (Galbraith) a delightful disection of economic hubris (and the need for stabilizing controls that we long since did away with).
• The Rise and Fall of the Third Reich (William Shirer) detailing exactly how things went wrong in Germany after the Great Depression.
• Witch hunting in Scotland (Brian Levack) on the Scottish experience of the great European witchcraft panic (James I/VI wrote a treatise on Witchcraft).
• Wood and Thomas paper on the problems of prediction with disease models in the absense of direct validation data (the least impressive item here).

Pythonでポートフォリオ最適化（マーコビッツの平均分散モデル）

Pythonでbacktestする際のTipsをまとめたものです．面倒な前処理をさくっと終わらせてモデル作りに専念しましょう！という主旨です．記事では紹介していませんが，pandas-datareaderでマクロデータもだいたい取れるので， 複数因子モデルなど，さまざまなポートフォリオ選択モデルを試すことができます．

Overview

• PythonでBacktestする環境を整える．
• 東証TOPIX構成銘柄から対象資産を選び最小分散ポートフォリオを組む．

株価データの取得

まず，pandas-datareaderを環境にインストールします．

pandas-datareaderは，株価などの市場データをWeb API経由でダウンロードできる（pandas.Dataframe friendlyで）便利なPythonパッケージです．IEX, World Bank, OECD, Yahoo! Finance，FRED，StooqなどのAPIを内部で叩き、pythonコード上に取得したデータを読み込みことができます．詳しい使い方は公式ドキュメントを参照してください．

# Install pandas-datareader (latest version)pip install git+https://github.com/pydata/pandas-datareader.git# Or install pandas-datareader (stable version)
pip install pandas-datareader

今回は，東京証券取引所（東証）に上場している株式銘柄を対象商品とします． Web上で公開されているデータは圧倒的に米国市場のものが多いですが，ポーランドの最強サイトstooq.comは東京証券取引所の過去データを公開しています．pandas-datareaderを使ってstooq から個別銘柄のデータを取得しましょう．

基本的には，pandas_datareader.stooq.StooqDailyReader()を実行すればOKです．引数には，各市場に登録してある証券コード(or ティッカーシンボル)と、データ公開元のサイト(Yahoo!, Stooq, ...)を指定します．

東京証券取引所で取り扱いされている株式銘柄には，4桁の証券コードが割り当てられているので、今回はこれを使います．（例：トヨタ自動車の株式は、東証で は証券コードが7203である銘柄として，NYSEではティッカーシンボルがTMである銘柄として取引されています．）

試しに，トヨタ自動車(東証:7203)の株価データを取得してプロットしてみましょう，

import datetime
import pandas_datareader

start = datetime.datetime(2015, 1, 1)
end = datetime.datetime(2020, 11, 30)
stockcode = "7203.jp" # Toyota Motor Corporation (TM)

df = pandas_datareader.stooq.StooqDailyReader(stockcode, start, end).read()
df = df.sort_values(by='Date',ascending=True)
display(df) # Show dataframe
-----
            Open        High    Low         Close       Volume
Date
2015-01-05      6756.50 6765.42 6623.43 6704.69 10653925
2015-01-06      6539.48 6601.09 6519.83 6519.83 13870266
2015-01-07      6480.52 6685.05 6479.64 6615.40 12837377
2015-01-08      6698.46 6748.46 6693.98 6746.69 11257646
2015-01-09      6814.56 6846.70 6752.92 6795.80 11672928
...     ...     ...     ...     ...     ...
2020-11-04      7024.00 7054.00 6976.00 6976.00 6278100
2020-11-05      6955.00 7032.00 6923.00 6984.00 5643400
2020-11-06      7070.00 7152.00 7015.00 7019.00 11092900
2020-11-09      7159.00 7242.00 7119.00 7173.00 7838600
2020-11-10      7320.00 7360.00 7212.00 7267.00 8825700

日別の株価推移データがpandas.Dataframeとして取得できました！ いま作成したdfの中身をプロットしてみます．（基本的に終値をつかいます）

# Plot timeseries (2015/1/1 - 2020/11/30)
plt.figure(figsize=(12,8))
plt.plot(df.index, df["Close"].values)
plt.show()

下図のように，終値(Close)の推移が簡単にプロットできました．

対象資産のパネルデータを作る

ポートフォリオ最適化問題を解くための準備として，複数の資産(株式銘柄)に対するパネルデータを作り，pandas.Dataframeオブジェクトとして整理します．

今回はTOPIX 500に掲載されている銘柄から5つ選び，投資対象資産とします．また，前処理として「終値」を「終値ベースの収益率」へ変換しています．この部分のコ ードは状況に合わせて変えてください．

import datetime
import numpy as np
import pandas as pd
import pandas_datareader.data as web
import pandas_datareader.stooq as stooq


def get_stockvalues_tokyo(stockcode, start, end, use_ratio=False):
    """
    stockcode: market code of each target stock (ex. "NNNN") defined by the Tokyo stock market.
    start, end: datetime object
    """
    # Get index data from https://stooq.com/
    df = stooq.StooqDailyReader(f"{stockcode}.jp", start, end).read()
    df = df.sort_values(by='Date',ascending=True)

    if use_ratio:
        df = df.apply(lambda x: (x - x[0]) / x[0] )
    return df

def get_paneldata_tokyo(stockcodes, start, end, use_ratio=False):
    # Use "Close" value only
    dfs = []
    for sc in stockcodes:
        df = get_stockvalues_tokyo(sc, start, end, use_ratio)[['Close']]
        df = df.rename(columns={'Close': sc})
        dfs.append(df)
    df_concat = pd.concat(dfs, axis=1)
    return df_concat

get_paneldata_tokyo()を使ってパネルデータを作成します．

start = datetime.datetime(2015, 1, 1)
end = datetime.datetime(2020, 11, 30)
stockcodes=["1301", "1762", "1820", "1967", "2127"]

df = get_paneldata_tokyo(stockcodes, start, end, use_ratio=True)
display(df) # return ratio daily
-----
            1301            1762        1820            1967        2127
Date
2015-01-05      0.000000        0.000000        0.000000        0.000000        0.000000
2015-01-06      -0.010929       -0.018385       -0.033937       -0.002265       -0.038448
2015-01-07      -0.014564       -0.020433       -0.059863       -0.013823       -0.059680
2015-01-08      -0.007302       -0.016338       -0.057883       -0.013823       -0.039787
2015-01-09      0.000000        -0.004490       -0.031938       -0.025407       -0.043770
...     ...     ...     ...     ...     ...
2020-10-29      0.096138        -0.032923       -0.030777       0.858573        5.682321
2020-10-30      0.093336        -0.039657       -0.041199       0.832831        5.704266
2020-11-02      0.107748        -0.026188       -0.032198       0.845702        5.418978
2020-11-04      0.099341        -0.024392       -0.020829       0.858573        5.704266
2020-11-05      0.069315        -0.014964       -0.042147       0.904909        6.055390

これで，評価対象となる各資産のパネルデータを取得できました．

マーコビッツの平均分散モデルとその解法

投資対象となる複数の資産に対して，適当な投資比率をそれぞれ決定することをポートフォリオ最適化といいます．今回は，最も基本的なポートフォリオ最適化の問題設定として，Markowitzが提唱した平均分散モデル(Mean-Variance Model)を採用します．

Markowitzの平均分散モデル

Markowitzの平均分散モデルでは，「ポートフォリオの期待収益率(Expected return)が一定値以上となる」という制約条件の下で，「ポートフォリオの分散を最小化する」最適化問題を考えます．

一般に，コの資産で構成されるポートフォリオの場合，ポートフォリオの分散はコの資産間の共分散行列の二次形式となるので，この最適化問題は二次計画問題(Quadratic Programming, QP)のクラスとなり，次のように定式化されます．

• ー コの資産の共分散行列
• ー コの資産の投資比率ベクトル
• ー コの資産の期待収益率ベクトル
• ー 資産の投資比率
• ー 資産の期待収益率
• ー 投資家の要求期待収益率
• ー ポートフォリオの収益率の期待値
• ー ポートフォリオの収益率の標準偏差

1つ目の制約式は，ポートフォリオの期待収益率が一定値()以上となることを要請しています．2つ目，3つ目の制約式はポートフォリオの定義からくる自明なものです．資産の空売りを許す場合，3つ目の 制約式を除くこともあります．

CVXOPTの使い方

Pythonの凸最適化向けパッケージCVXOPTを使って，この二次計画問題(QP)を解きます． CVXOPTで二次計画問題を扱う場合は，解きたい最適化問題を以下の一般化されたフォーマットに整理して，

パラメータP,q,G,h,Aを計算し，cvxopt.solvers.qp()関数を実行することで最適解と最適値を求めます．Markowitzの平均・分散モデルの場合は，

となります．

参考: - https://cvxopt.org/userguide/coneprog.html#quadratic-programming - https://qiita.com/ryoshi81/items/8b0c6add3e367f94c828

Pythonで計算

対象資産のパネルデータdfから，必要な統計量を計算します．

ポートフォリオ内の資産間の共分散行列 ：

df.cov() # Covariance matrix
-----
        1301        1762        1820        1967            2127
1301    0.024211        0.015340        0.018243        0.037772        0.081221
1762    0.015340        0.014867        0.015562        0.023735        0.038868
1820    0.018243        0.015562        0.025023        0.029918        0.040811
1967    0.037772        0.023735        0.029918        0.109754        0.312827
2127    0.081221        0.038868        0.040811        0.312827        1.703412

ポートフォリオ内の各資産の期待収益率 ：

df.mean().values # Expected returns
-----
array([0.12547322, 0.10879767, 0.07469455, 0.44782516, 1.75209493])

CVXOPTを使って最適化問題を解く．

import cvxopt

def cvxopt_qp_solver(r, r_e, cov):
    # CVXOPT QP Solver for Markowitz' Mean-Variance Model
    # See https://cvxopt.org/userguide/coneprog.html#quadratic-programming
    # See https://cdn.hackaday.io/files/277521187341568/art-mpt.pdf
    n = len(r)
    r = cvxopt.matrix(r)

    P = cvxopt.matrix(2.0 * np.array(cov))
    q = cvxopt.matrix(np.zeros((n, 1)))
    G = cvxopt.matrix(np.concatenate((-np.transpose(r), -np.identity(n)), 0))
    h = cvxopt.matrix(np.concatenate((-np.ones((1,1)) * r_e, np.zeros((n,1))), 0))
    A = cvxopt.matrix(1.0, (1, n))
    b = cvxopt.matrix(1.0)
    sol = cvxopt.solvers.qp(P, q, G, h, A, b)
    return sol

r = df.mean().values # Expected returns
r_e = 0.005 * # Lower bound for portfolio's return
cov = df.cov() # Covariance matrix

# Solve QP and derive optimal portfolio
sol = cvxopt_qp_solver(r, r_e, cov)
x_opt = np.array(sol['x'])
print(x_opt)
print("Variance (x_opt) :", sol["primal objective"])

-----

 pcost       dcost       gap    pres   dres
 0:  4.3680e-03 -8.6883e-02  5e+00  2e+00  2e+00
 1:  9.1180e-02 -2.2275e-01  5e-01  1e-01  1e-01
 2:  2.1337e-02 -6.0274e-02  8e-02  2e-16  1e-16
 3:  1.0483e-02 -1.7810e-03  1e-02  1e-16  3e-17
 4:  4.9857e-03  1.5180e-03  3e-03  2e-16  8e-18
 5:  4.0217e-03  3.6059e-03  4e-04  3e-17  1e-17
 6:  3.7560e-03  3.7107e-03  5e-05  3e-17  1e-18
 7:  3.7187e-03  3.7168e-03  2e-06  1e-17  4e-18
 8:  3.7169e-03  3.7168e-03  2e-08  1e-16  6e-18
Optimal solution found.
[ 5.56e-05]
[ 1.00e+00]
[ 1.76e-05]
[ 3.84e-07]
[ 2.63e-07]

Variance (x_opt):  0.003716866155475511 # 最適ポートフォリオの分散

最適解（各資産への最適な投資比率）と，最適値（最適な投資比率を適用した場合のポートフォリオの分散）が求められました．なお，今回使った平均分散モデルによる最適解はポートフォリオのリスク(分散)に対する最適性を重視 しているので，「最小分散ポートフォリオ」と呼ばれます．

なお，収益率に対する評価指標には，無リスク資産の収益率(インフレ率)を加味したシャープレシオを用いるケースが多いです．backtestの方法についてはいくつか流儀があるので，専門書や論文を参照してください．

おまけ:

上のコードをまとめて，自作のバックテスト用PythonクラスMarkowitzMinVarianceModel()を作りました． 以下は参考例です．

バックテスト用のPythonクラス

import cvxopt
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

class MarkowitzMinVarianceModel():
    """
    Args:
    =====
    - df: pandas.dataframe
        panel data for target assets for the portfolio.
            its index must be `numpy.datetime64` type.
            its columns must be time-series data of target assets.
    - window_size: int
        the size of time-window which is used when deriving (or updating) the portfolio.
    - rebalance_freq: int
        rebalance frequency of the portfolio.
    - r_e: float
        min of the return ratio (= capital gain / investment).
    - r_f: float
        rate of returns of the risk-free asset.
    """
    def __init__(self, df, window_size, rebalance_freq, r_e=None, r_f=None):
        self.df = self._reset_index(df)
        self.df_chg = self.df.pct_change()
        self.df_chg[:1] = 0.0 # set 0.0 to the first record
        self.df_bt = None
        self.df_bt_r = None
        self.df_bt_x = None
        self.window_size = window_size
        self.rebalance_freq = rebalance_freq
        self.jgb_int = 0.0001 # 0.01% per year (Japanese Government Bond)
        self.r_f = r_f if r_f is not None else self.jgb_int * (1/12) # adjust monthly
        self.r_e = r_e if r_e is not None else r_f

    def _reset_index(self, df):
        df = df.copy()
        df['date'] = pd.to_datetime(df.index)
        df = df.set_index('date')
        return df

    def get_dfbt_r(self):
        return self.df_bt_r

    def get_dfbt_x(self):
        return self.df_bt_x

    def backtest(self):
        date_init = self.df.index.values[self.window_size]
        df_bt = pd.DataFrame([[0.0, np.nan]], index=[date_init], columns=['ror', 'std'])
        df_bt_r = pd.DataFrame(columns=list(self.df.columns.values))
        df_bt_x = pd.DataFrame(columns=list(self.df.columns.values))
        for idx, date in enumerate(self.df.index.values):
            if idx >= self.window_size + self.rebalance_freq:
                if (idx - self.window_size) % self.rebalance_freq == 0:
                    # df_chg_train
                    st = idx - self.rebalance_freq - self.window_size
                    ed = idx - self.rebalance_freq
                    df_chg_train = self.df_chg[st:ed]

                    # expected returns per target term
                    if isinstance(self.r_e, pd.core.frame.DataFrame):
                        r_e = self.r_e.iloc[st:ed].values.mean()
                    else:
                        r_e = self.r_e

                    # x_p: min variance portfolio
                    x_p = self.calc_portfolio(df_chg_train, r_e)

                    # df_chg_test
                    st = idx - self.rebalance_freq
                    ed = idx
                    df_chg_test = self.df_chg[st:ed]
                    df_chgcum_test = (1.0 + df_chg_test).cumprod() - 1.0

                    # ror_p: rate of return (portfolio)
                    ror_test = df_chgcum_test.iloc[-1].values
                    ror_p = float(np.dot(ror_test, x_p))
                    df_bt_r.loc[date] = ror_test
                    df_bt_x.loc[date] = x_p

                    # std (portfolio)
                    if self.rebalance_freq == 1:
                        std_p = np.nan
                    else:
                        std_test = df_chg_test.std(ddof=True).values
                        std_p = float(np.dot(std_test, np.abs(x_p)))

                    # append
                    df_one = pd.DataFrame([[ror_p, std_p]], index=[date], columns=df_bt.columns)
                    df_bt = df_bt.append(df_one)

        # reset index
        self.df_bt = self._reset_index(df_bt)
        self.df_bt_r = self._reset_index(df_bt_r)
        self.df_bt_x = self._reset_index(df_bt_x)
        return self.df_bt

    def calc_portfolio(self, df_retchg, r_e):
        r = df_retchg.mean().values
        cov = np.array(df_retchg.cov())
        x_opt = self.cvxopt_qp_solver(r, r_e, cov)
        return x_opt

    def cvxopt_qp_solver(self, r, r_e, cov):
        """
        CVXOPT QP Solver for Markowitz' Mean-Variance Model
        - See also https://cvxopt.org/userguide/coneprog.html#quadratic-programming
        - See also https://cdn.hackaday.io/files/277521187341568/art-mpt.pdf

        r: mean returns of target assets. (vector)
        r_e: min of the return ratio (= capital gain / investment).
        cov: covariance matrix of target assets. (matrix)
        """
        n = len(r)
        r = cvxopt.matrix(r)

        # Create Objective matrices
        P = cvxopt.matrix(2.0 * np.array(cov))
        q = cvxopt.matrix(np.zeros((n, 1)))

        # Create constraint matrices
        G = cvxopt.matrix(np.concatenate((-np.transpose(r), -np.eye(n)), 0))
        h = cvxopt.matrix(np.concatenate((-np.ones((1,1))*r_e, np.zeros((n,1))), 0))
        A = cvxopt.matrix(1.0, (1, n))
        b = cvxopt.matrix(1.0)

        # Adjust params (stop log messages)
        cvxopt.solvers.options['show_progress'] = False # default: True
        cvxopt.solvers.options['maxiters'] = 1000 # default: 100

        sol = cvxopt.solvers.qp(P, q, G, h, A, b)
        x_opt = np.squeeze(np.array(sol['x']))
        return x_opt

    def get_yearly_performance(self):
        if self.df_bt is None:
            pass
        else:
            df_yearly = self.df_bt[["ror"]].resample('y').sum()
            df_yearly["std"] = self.df_bt["ror"].resample('y').std().values
            df_yearly["sharpe_ratio"] = df_yearly.apply(lambda d: (d["ror"] - self.r_f) / d["std"], axis=1)
            return df_yearly

    def evaluate_backtest(self, logging=False):
        if self.df_bt is None:
            pass
        else:
            self.r_mean = self.df_bt["ror"].mean()
            self.r_std = self.df_bt["ror"].std(ddof=True)
            self.sharpe_ratio = (self.r_mean - self.r_f) / self.r_std
            self.net_capgain = (self.df_bt["ror"] + 1.0).cumprod().iloc[-1] - 1.0

            self.r_mean_peryear = 12 * self.r_mean
            self.r_std_peryear = np.sqrt(12) * self.r_std
            self.sharpe_ratio_peryear = (self.r_mean_peryear - self.jgb_int) / self.r_std_peryear

            if logging:
                print("Portfolio Performance")
                print("=======================")
                print("Returns per month")
                print("  sharpe ratio     : {:.8f}".format(self.sharpe_ratio))
                print("  mean of returns  : {:.8f}".format(self.r_mean))
                print("  std of returns   : {:.8f}".format(self.r_std))
                print("    risk-free rate : {:.8f}".format(self.r_f))
                print("    capgain ratio  : {:.8f}".format(self.net_capgain))
                print("Returns per year")
                print("  sharpe ratio     : {:.8f}".format(self.sharpe_ratio_peryear))
                print("  mean of returns  : {:.8f}".format(self.r_mean_peryear))
                print("  std of returns   : {:.8f}".format(self.r_std_peryear))


    def plot_returns(self):
        if self.df_bt is None:
            pass
        else:
            xlabels = [d.strftime('%Y-%m') for idx, d in enumerate(self.df_bt.index) if idx % 12 == 0]

            fig, ax = plt.subplots(figsize=(12,6))
            ax.plot(self.df_bt.index.values, self.df_bt["ror"].values, label="rate of returns")
            ax.plot(self.df_bt.index.values, self.df_bt["ror"].cumsum().values, label="total capital gain ratio")
            ax.legend(loc="upper left")
            ax.set_xticks(xlabels)
            ax.set_xticklabels(xlabels, rotation=40)
            return fig

    def plot_returns_histgram(self):
        if self.df_bt is None:
            pass
        else:
            x = self.df_bt["ror"].values
            r_mean = "{:.4f}".format(x.mean())
            r_std = "{:.4f}".format(x.std())

            fig, ax = plt.subplots(figsize=(12,6))
            ax.hist(x, bins=30, alpha=0.75)
            ax.set_title(f"mean={r_mean}, std={r_std}")
            return fig

使い方

対象資産としてTOPIX Core30に含まれる内国株30銘柄を選び，これらに(最適な)投資比率を与えてバックテストしてみましょう．

まず，pandas_datareader.data.DataReaderでTOPIX Core30構成銘柄のヒストリカルデータを読み込んで，すこし整形します．¹

6502, 6752, 6758, 6954, 7201, 7203, 7267, 7751, 8031, 8058, 8306, 8316, 8411, 8604, 8766, 8802, 9021, 9432, 9433, 9437, 9984]`としてください．

# Get historical data
st = '2004/10/31' # start date
ed = '2020/10/31' # end date
stocks_topix30 = [2914, 3382, 4063, 4452, 4502,
                  4503, 5401, 6301, 6501, 6502,
                  6752, 6758, 6954, 7201, 7203,
                  7267, 7751, 8031, 8058, 8306,
                  8316, 8411, 8604, 8766, 8802,
                  9021, 9432, 9433, 9437, 9984] # list of tickers in TOPIX Core30
symbols =  [str(s)+'.T' for s in stocks_topix30]
dfs = []
for symbol in symbols:
    df = pandas_datareader.data.DataReader(symbol, 'yahoo', st, ed) # daily
    df = df.resample('M').mean() # daily -> monthly
    df = df.sort_values(by='Date', ascending=True)
    df = df.fillna(method='ffill') # 1つ前の行の値で埋める
    df = df[['Close']].rename(columns={'Close': symbol})
    dfs.append(df)
df_tpx30 = pd.concat(dfs, axis=1)

# fill nan
for col in df_tpx30.columns:
    st_idx = df_tpx30[col].first_valid_index()
    ed_idx = df_tpx30[col].last_valid_index()
    # for any columns (stocks)
    if df_tpx30[col].isnull().any():
        # New listing (新規上場)
        if st_idx != df_tpx30.index[0]:
            df_tpx30[col] = df_tpx30[col].fillna(df_tpx30[col][st_idx])
        # Delisting (上場廃止)
        if df_tpx30.index[-1] != ed_idx:
            df_tpx30[col] = df_tpx30[col].fillna(df_tpx30[col][ed_idx])

こんな感じのパネルデータができれば準備OK．

df_tpx30.tail()

Date        2914.T          3382.T          4063.T          4452.T          4502.T          4503.T          5401.T          6301.T          6501.T          6502.T      ...     8316.T      8411.T          8604.T          8766.T      8802.T      9021.T      9432.T      9433.T          9437.T          9984.T

2020-06-30      2147.159091     3710.272727     12471.136364    8774.045455     4024.818182     1824.386364     1063.240909     2220.500000     3561.590909     3275.681818     ...     3172.181818     1363.545455     486.763636      4795.681818     1701.840909     6502.181818     2500.454545     3184.863636     2913.454545     5287.318182
2020-07-31      1933.785714     3427.333333     12802.619048    8465.428571     3763.000000     1731.785714     998.023810      2239.047619     3371.714286     3450.714286     ...     3029.809524     1347.857143     491.138096      4699.238095     1576.000000     5405.428571     2523.428571     3289.142857     2944.547619     6311.333333
2020-08-31      1995.300000     3399.050000     12785.500000    8041.000000     3967.150000     1712.075000     1009.300000     2207.650000     3489.050000     3351.750000     ...     3023.050000     1402.250000     531.764998      4779.850000     1644.575000     5106.050000     2570.875000     3285.300000     3066.400000     6453.700000
2020-09-30      1970.425000     3357.000000     13804.250000    8053.550000     3898.200000     1622.550000     1073.164999     2352.600000     3631.650000     2941.300000     ...     3090.425000     1402.175000     522.770003      4871.900000     1638.575000     5578.100000     2313.800000     2851.150000     2879.875000     6278.600000
2020-10-31      1989.095238     3412.714286     14189.761905    7731.619048     3568.904762     1489.047619     1070.538095     2432.285714     3605.000000     2783.952381     ...     2969.428571     1311.571429     487.642857      4804.000000     1611.214286     4938.571429     2237.142857     2742.738095     3882.095238     6991.047619

あとは，自作クラスMarkowitzMinVarianceModel()のインスタンスオブジェクトmodelにパラメータと価格データdf_tpx30を食わせてバックテストを実行．

from datetime import datetime

# Const.
ST_BACKTEST = datetime(2011,10,31) # Investment period (start date)
ED_BACKTEST = datetime(2020,10,31) # Investment period (end date)

# Params
params = {
    "window_size": 12, # 収益率の特性量(平均，分散)の推定に使う期間 (ex. 運用時から過去36カ月)
    "rebalance_freq": 1, # リバランスの頻度 (1か月ごとにポートフォリオ内の投資比率を変更)
    "r_f": 0.0001 * (1/12) # リスクフリーレート (日本国債10年物利回り:0.01%を単利計算で月次に変換)
}

# Data
st = (ST_BACKTEST - relativedelta(months=params["window_size"])).strftime('%Y-%m-%d')
ed = ED_BACKTEST.strftime('%Y-%m-%d')
df = df_tpx30[st:ed]
params["r_e"]=  df_tpx[st:ed] # 要求期待収益率(r_e)は同時期のTOPIX Indexの収益率とする (df_tpx作成コードは省略)

# Create model
model = MarkowitzMinVarianceModel(df, **params)

# Backtest by model
df_bt = model.backtest()

ここからは，自作クラスMarkowitzMinVarianceModel()に用意したバックテスト評価用のメソッドを使う．(分析は無限大)

ポートフォリオのパフォーマンス評価

# Evaluate
model.evaluate_backtest(logging=True)

Portfolio Performance
=======================
Returns per month
  sharpe ratio     : 0.18788996
  mean of returns  : 0.00735206
  std of returns   : 0.03908527
    risk-free rate : 0.00000833
    capgain ratio  : 1.04714952
Returns per year
  sharpe ratio     : 0.65086993
  mean of returns  : 0.08822476
  std of returns   : 0.13539535

ポートフォリオの収益率・累積収益率プロット

fig = model.plot_returns() # Plot returns

ポートフォリオの月次収益率分布

fig = model.plot_returns_histgram()

ポートフォリオの年次パフォーマンス

df_yearly = model.get_yearly_performance()
df_yearly

date            ror         std             sharpe_ratio
2011-12-31      -0.0001 3.3888e-05      -3.6736
2012-12-31      -0.0444 1.2435e-02      -3.5695
2013-12-31      0.5524  6.5010e-02      8.4973
2014-12-31      0.2448  5.2800e-02      4.6357
2015-12-31      0.0952  4.1543e-02      2.2923
2016-12-31      -0.0970 4.0639e-02      -2.3871
2017-12-31      0.2486  3.0262e-02      8.2144
2018-12-31      -0.0097 3.6705e-02      -0.2644
2019-12-31      0.0254  3.1904e-02      0.7947
2020-12-31      -0.1793 7.3461e-02      -2.4404

ポートフォリオ内の各銘柄の収益率(%)

df_bt_r = model.get_dfbt_r() # rate_of_returns
df_bt_x = model.get_dfbt_x() # investment_ratio

df1 = df_bt_r * df_bt_x # (rate_of_returns) × (investment_ratio)

df1 = df1.resample("y").sum()
df1.columns = [c.replace(".T", "") for c in df1.columns]
df1 = df1.T * 100 # transpose && convert as pct.
df1.columns = [c.strftime('%Y') for c in df1.columns]

plt.figure(figsize=(12,12))
sns.heatmap(df1, cmap="RdBu", center=0, annot=True, fmt=".2f", cbar=True)
plt.show()

最後まで読んでいただき，ありがとうございます！

Pythonによるファイナンス 第2版 ―データ駆動型アプローチに向けて (オライリー・ジャパン)

ファイナンス機械学習―金融市場分析を変える機械学習アルゴリズムの理論と実践

Pythonによる ファイナンス入門 (実践Pythonライブラリー)

経済・ファイナンスデータの計量時系列分析 (統計ライブラリー)

ファイナンスのための計量分析

道具としてのファイナンス

---

1. stocks_topix30はTOPIX Core30構成銘柄の証券コードのリストです．構成銘柄は毎年10/31に更新されます．サンプルコードを再現したい場合`stocks_topix30 = [2914, 3382, 4063, 4452, 4502, 4503, 5401, 6301, 6501, ↩

Jupyter notebookの出力セルの大きさを無限にする

TL;DR

以下のマジックコマンド（Cell magic）をセルに入れて実行。

%%javascript
IPython.OutputArea.auto_scroll_threshold = 9999;

注意：%matplotlib inlineのようなLine magicではないので，独立したセルを用意して実行しないとエラーが発生する．詳しくはIPythonの公式ドキュメント 参照．

• % - All available line magic commands - check here
• %% - All available cell magic commands - check here

Cf.

• Magic functions - IPython公式ドキュメント
• comment:53708976 issue:2172 ipython github.com
• ipythonノートブックの出力ウィンドウのサイズを変更する
• Jupyter notebookで列をすべて表示したい - Qitta

EMアルゴリズム

　EM アルゴリズムは，不完全データに基づく統計モデル一般に適用される，最尤推定量を導出するためのアルゴリズムです． もともと，「不完全データ・完全データ」という概念は欠損データの問題に対処するために立てられましたが，定義を拡張することで，切断データ・打ち切りデータ・混合分布モデル・ロバスト分布モデル・潜在変数モデル・ベイズモデルなどにも適用できます．

　クラスタリングや教師なし学習に用いられる多くの手法（例：k-means，混合ガウス分布モデル）は，計算過程に着目するとEMアルゴリズムとして一般化できます．さらに，情報幾何の観点からEMアルゴリズムを解析した研究も盛んで，指数分布族をもつ確率モデルに対するEMアルゴリズムの適用は，e-射影/m-射影という形式でまとめられます．

1. 統計的推測

目的：ある変数 が従う確率分布 を求めたい．

このとき，パラメータで決定される確率モデルを考え，コのデータサンプル から最適なパラメータ を選ぶことで

$$ x \sim q(x) \approx p(x|\theta) $$

という近似式を成り立たせたい．これを統計的推測（推定）という．

2. 最尤推定

統計的推測の最も基本的なアルゴリズムは最尤推定である．対数尤度関数:

$$ \ell(\theta | x) := \log p(x | \theta) $$

を定義して，コのデータサンプル から，

$$ J(\theta) := \frac{1}{n} \sum_{i=1}^{n} \ell(\theta | x_i), ~~~ \hat{\theta}_{MLE} = \underset{\theta \in \Theta}{\rm argmax} ~ J(\theta) $$

を解けば，パラメータ の最尤推定量 を求めることができる．

3. EMアルゴリズム

• 完全データ :
  
  • 観測不可能だが，求めたい確率分布p(x)に完全に従うデータ．
• 不完全データ :
  
  • 観測可能だが，求めたい確率分布p(x)に完全に従わないデータ．

を考える．完全データ と不完全データの関係は一般に「１() 対 多()」となるが，ここでは応用上都合の良い仮定として，潜在変数 を用いてこれを表す．すなわち， と仮定する．

このとき，完全データ の確率モデル：

$$ p(x | \theta) = p(y, z | \theta) $$

を考える，ここで，変数 のデータサンプルは観測できないため尤度関数 は計算できないが，変数 のデータサンプルは観測できることを利用して，

$$ \begin{eqnarray} p(y | \theta) &=& \int_{Z} p(x | \theta) ~ dz \\ &=& \int_{Z} p(y, z | \theta) ~ dz \end{eqnarray} $$

という量を考える．このとき，

変数 が従う確率分布 を近似する確率モデル を定める

ための計算法としてEMアルゴリズムが登場する．具体的には以下の通り．

1. 初期値を与える．
2. For each step :
   

   • E step
     期待値（Expectation）を計算する． $$ Q(\theta | \theta^{(t)}) = \mathbb{E}_{x \sim p(x|\theta)} \left[ \log p(x|\theta) | y, \theta^{(t)} \right] $$

   • M step
     期待値 を最大化（Maximzation）するパラメータを求める． $$ \theta^{(t+1)} = \underset{\theta \in \Theta}{\rm argmax} ~ Q(\theta | \theta^{(t)}) $$

3. 収束した値 を推定値 とし，確率モデル を得る．

E step と M step で行う計算をまとめると，

• EM step
  $$ \begin{eqnarray} \theta^{(t+1)} &=& \underset{\theta \in \Theta}{\rm argmax} ~ \mathbb{E}_{x \sim p(x|\theta)} \left[ \log p(x | \theta) | y, \theta^{(t)} \right] \\ &=& \underset{\theta \in \Theta}{\rm argmax} ~ \mathbb{E}_{(y,z) \sim p(y,z|\theta)} \left[ \log p(y, z | \theta) | y, \theta^{(t)} \right] \\ &=& \underset{\theta \in \Theta}{\rm argmax} ~ \mathbb{E}_{z | {\theta}^{(t)} \sim \int_{Y} p(y,z | {\theta}^{(t)}) dy} \left[ \log p(y, z | \theta) \right] \\ \end{eqnarray} $$

となる．

参考文献

• 9章 EMアルゴリズム - 「21 世紀の統計科学」第 III 巻 日本統計学会, 2008
• 解説 EMアルゴリズムの幾何学 - 赤穂昭太郎, 電子技術総合研究所
• EMアルゴリズムと神経回路網, 2000, 統計数理研究所

続・わかりやすいパターン認識―教師なし学習入門―

EMアルゴリズムと不完全データの諸問題

計算統計学の方法―ブートストラップ・EMアルゴリズム・MCMC (シリーズ予測と発見の科学 5)

計算統計 I―確率計算の新しい手法 (統計科学のフロンティア 11)

統計科学のフロンティア 12　計算統計II　マルコフ連鎖モンテカルロ法とその周辺 (岩波オンデマンドブックス)

サーモス 真空断熱タンブラー 2個セット 400ml ステンレス JDI-400P S

2019上半期・買った本/読んだ本まとめ

2019年上半期に読んだ本。

新書・文庫本

問題解決の心理学―人間の時代への発想 (中公新書 (757))

「カッコいい」とは何か (講談社現代新書)

はじめて考えるときのように 「わかる」ための哲学的道案内 (PHP文庫)

自分を知るための哲学入門 (ちくま学芸文庫)

【新版】日本語の作文技術 (朝日文庫)

社会学史 (講談社現代新書)

話題・啓蒙

サピエンス全史(上)文明の構造と人類の幸福

ホモ・デウス 上: テクノロジーとサピエンスの未来

〈インターネット〉の次に来るもの　未来を決める１２の法則

ゲンロン0 観光客の哲学

ミクロ経済学の力

Google PageRankの数理 ―最強検索エンジンのランキング手法を求めて―

理工学

自己組織化と進化の論理―宇宙を貫く複雑系の法則 (ちくま学芸文庫)

経済・ファイナンスデータの計量時系列分析 (統計ライブラリー)

カーネル多変量解析―非線形データ解析の新しい展開 (シリーズ確率と情報の科学)

一般システム理論――その基礎・発展・応用

工学のための関数解析 (工学のための数学)

機械学習スタートアップシリーズ　Ｐｙｔｈｏｎで学ぶ強化学習　入門から実践まで (ＫＳ情報科学専門書)

ベイズ統計の理論と方法

入門 確率解析とルベーグ積分

統計力学〈1〉 (新物理学シリーズ)

数学ガール/フェルマーの最終定理 (数学ガールシリーズ 2)

数学ガール/ポアンカレ予想 (「数学ガール」シリーズ6)

「集合と位相」をなぜ学ぶのか ― 数学の基礎として根づくまでの歴史

オートポイエーシス―第三世代システム

情報系

UNIXという考え方―その設計思想と哲学

[試して理解]Linuxのしくみ ~実験と図解で学ぶOSとハードウェアの基礎知識

Webを支える技術 -HTTP、URI、HTML、そしてREST (WEB+DB PRESS plus)

詳解UNIXプログラミング 第3版

前処理大全[データ分析のためのSQL/R/Python実践テクニック]

機械学習のための特徴量エンジニアリング ―その原理とPythonによる実践 (オライリー・ジャパン)

退屈なことはPythonにやらせよう ―ノンプログラマーにもできる自動化処理プログラミング

リーダブルコード ―より良いコードを書くためのシンプルで実践的なテクニック (Theory in practice)

Ubuntu 16.04.6 LTS (GNU/Linux, x86_64) のGPUマシンの設定・TF1.13.1 / CUDA10.0 / cuDNN7.4.2

- 最終更新：2019/11/07

クリーンブートしたUbuntu16.04LTS マシンに，NVIDIA GPUを導入し，CuDA・cuDNNをセットアップしました． おもにtensorflow-gpuを使うためです．導入過程で色々とつまづいたので，得た知識をこのポストにまとめておきます．

実行環境

最終的に完成したマシンの動作環境は下記の通りです． latest update : 2019/05/15

• OS : Ubuntu 16.04.6 LTS (GNU/Linux 4.4.0-145-generic x86_64)
• Memory : 16 GB
• CPU(x8) : Intel Core i7-6700 CPU @ 3.40GHz
• GPU(x1) : NVIDIA Geforce GTX 1080
  • NVIDIA CUDA : 10.0.130 (/usr/local/cuda-10.0/)
  • NVIDIA cuDNN : 7.4.2.24 (/usr/lib/x86_64-linux-gnu/libcudnn.so.7.4.2)
  • Python3 : 3.6.9 (/usr/bin/python3.6)
  • Python2 : 2.7.12 (/usr/bin/python)
    • tensorflow : 1.13.1 ($HOME/.local/lib/python3.6/site-packages)
    • tensorflow-gpu : 1.13.1 ($HOME/.local/lib/python3.6/site-packages)
    • keras : 2.2.4 ($HOME/.local/lib/python3.6/site-packages)

1. OS

• 方法1: unameコマンドを使う

unameコマンドを使うと，「OS名,ホスト名,OSリリース,OSバージョン,マシンアーキテクチャ,CPUタイプ,プラットフォーム,OS名」が順に表示される．

$ uname -a

Linux XXXX 4.4.0-145-generic #171-Ubuntu SMP Tue Mar 26 12:43:40 UTC 2019 x86_64 x86_64 x86_64 GNU/Linux

• 方法2: /etc/issueをみる

マシンの「Linuxディストリビューション」が表示される．今回はUbuntu16.04．

$ cat /etc/issue

Ubuntu 16.04.6 LTS \n \l

• 方法3: /etc/lsb-releaseをみる

$ cat /etc/lsb-release

DISTRIB_ID=Ubuntu
DISTRIB_RELEASE=16.04 DISTRIB_CODENAME=xenial DISTRIB_DESCRIPTION="Ubuntu 16.04.6 LTS"

• 方法4: /etc/os-releaseをみる

$ cat /etc/os-release

NAME="Ubuntu"
VERSION="16.04.6 LTS (Xenial Xerus)" ID=ubuntu ID_LIKE=debian PRETTY_NAME="Ubuntu 16.04.6 LTS" VERSION_ID="16.04" HOME_URL="http://www.ubuntu.com/" SUPPORT_URL="http://help.ubuntu.com/" BUG_REPORT_URL="http://bugs.launchpad.net/ubuntu/" VERSION_CODENAME=xenial UBUNTU_CODENAME=xenial

• 方法5: /proc/versionをみる

/proc/versionをみると，Linuxカーネルの詳細が確認できる．

$ cat /proc/version

Linux version 4.4.0-159-generic (buildd@lgw01-amd64-042) (gcc version 5.4.0 20160609 (Ubuntu 5.4.0-6ubuntu1~16.04.10) ) #187-Ubuntu SMP Thu Aug 1 16:28:06 UTC 2019

2. HDD

2.1. HDDデバイスの確認

• dfコマンド

$ df -h

Filesystem Size Used Avail Use% Mounted on
udev 7.8G 0 7.8G 0% /dev tmpfs 1.6G 34M 1.6G 3% /run /dev/sda1 214G 101G 103G 50% / tmpfs 7.9G 0 7.9G 0% /dev/shm tmpfs 5.0M 4.0K 5.0M 1% /run/lock tmpfs 7.9G 0 7.9G 0% /sys/fs/cgroup tmpfs 1.6G 64K 1.6G 1% /run/user/1001 /dev/loop0 89M 89M 0 100% /snap/core/7270 /dev/loop1 384K 384K 0 100% /snap/patchelf/61 /dev/loop2 384K 384K 0 100% /snap/patchelf/69

3. メモリ

3.1. メモリデバイスの確認

• /proc/meminfoをみる

/proc/meminfoをみると，メモリ容量の詳細を確認できる．

$ cat /proc/meminfo

MemTotal: 16377200 kB
MemFree: 3077848 kB
MemAvailable: 15767804 kB
Buffers: 363052 kB
Cached: 12274992 kB
SwapCached: 66936 kB
Active: 8048088 kB
Inactive: 4689560 kB
Active(anon): 25860 kB
Inactive(anon): 86584 kB
...
HugePages_Total: 0
HugePages_Free: 0
HugePages_Rsvd: 0
HugePages_Surp: 0
Hugepagesize: 2048 kB
DirectMap4k: 1907316 kB
DirectMap2M: 14815232 kB
DirectMap1G: 0 kB

3.2. 仮想メモリの状態確認

• 方法1: freeコマンド

freeを使う．

$ free

total used free shared buff/cache available
Mem: 16377148 300020 6661176 9876 9415952 15688968 Swap: 16720892 0 16720892

• 方法2: vmstatコマンド

vmstatを使う．

$ vmstat

procs -----------memory---------- ---swap-- -----io---- -system-- ------cpu-----
r b swpd free buff cache si so bi bo in cs us sy id wa st
2 0 90724 1771068 363852 9020168 322 295 335 492 1 1 2 0 97 1 0

• 方法3: topコマンド

topを使う．

$ top

top - 20:17:14 up 56 days, 1:17, 5 users, load average: 2.02, 1.99, 1.66
Tasks: 180 total, 3 running, 177 sleeping, 0 stopped, 0 zombie %Cpu(s): 25.0 us, 0.0 sy, 0.0 ni, 75.0 id, 0.0 wa, 0.0 hi, 0.0 si, 0.0 st KiB Mem : 16377200 total, 1078612 free, 5914516 used, 9384072 buff/cache KiB Swap: 16720892 total, 16630168 free, 90724 used. 10049856 avail Mem

PID USER PR NI VIRT RES SHR S %CPU %MEM TIME+ COMMAND
14461 xxxxxxx 20 0 54.634g 1.768g 12740 R 100.0 11.3 18:30.96 python3
14499 xxxxxxx 20 0 54.634g 1.752g 12448 R 100.0 11.2 17:54.35 python3
1 root 20 0 119680 4616 3084 S 0.0 0.0 0:31.51 systemd
2 root 20 0 0 0 0 S 0.0 0.0 0:00.20 kthreadd
3 root 20 0 0 0 0 S 0.0 0.0 0:05.32 ksoftirqd/0
5 root 0 -20 0 0 0 S 0.0 0.0 0:00.00 kworker/0:0H
7 root 20 0 0 0 0 S 0.0 0.0 18:07.52 rcu_sched
8 root 20 0 0 0 0 S 0.0 0.0 0:00.00 rcu_bh
9 root rt 0 0 0 0 S 0.0 0.0 0:00.25 migration/0
...

4. CPU

4.1. CPUデバイスの確認

• 方法1: /proc/cpuinfoをみる

# CPUデバイスの確認
$ cat /proc/cpuinfo

processor : 0
vendor_id : GenuineIntel
cpu family : 6
model : 94
model name : Intel(R) Core(TM) i7-6700 CPU @ 3.40GHz
stepping : 3
microcode : 0xc6
cpu MHz : 800.062
cache size : 8192 KB
physical id : 0
siblings : 8
...
processor : 1
vendor_id : GenuineIntel
cpu family : 6
model : 94
model name : Intel(R) Core(TM) i7-6700 CPU @ 3.40GHz
...

5. GPU

5.1. GPUデバイスの確認

• lshwコマンド

# GPUデバイスの確認
$ sudo lshw -C display 

*-display
詳細: VGA compatible controller
製品: GP104 [GeForce GTX 1080]
ベンダー: NVIDIA Corporation
物理ID: 0
バス情報: pci@0000:01:00.0
バージョン: a1
幅: 64 bits
クロック: 33MHz
性能: pm msi pciexpress vga_controller bus_master cap_list rom
設定: driver=nvidia latency=0
リソース: irq:16 メモリー:de000000-deffffff メモリー:c0000000-cfffffff メモリー:d0000000-d1ffffff IOポート:e000(サイズ=128) メモリー:df000000-df07ffff

• lspciコマンド

lspciでハードウェアデバイス一覧が確認できる．

# GPUデバイスの確認
$ lspci  | grep -i nvidia 

01:00.0 VGA compatible controller: NVIDIA Corporation GP104 [GeForce GTX 1080] (rev a1)
01:00.1 Audio device: NVIDIA Corporation GP104 High Definition Audio Controller (rev a1)

5.2. NVIDIA ドライバ

下記のリンクから，自分のGPUにあうドライバを検索して，ダウンロードする．

• https://www.nvidia.co.jp/Download/index.aspx?lang=jp

今回，NVIDIA GeForce 1080に対応したドライバ情報は以下のようになった．

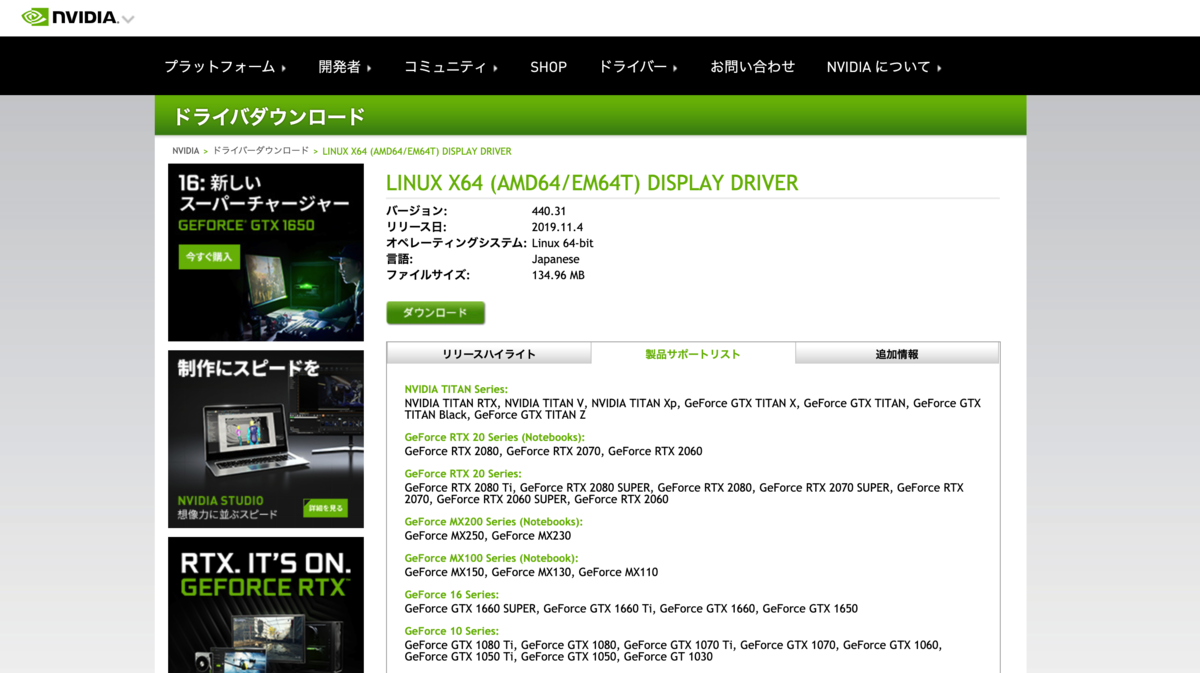
新しくGPUドライバ（NVIDIAドライバ）をインストールする前に，すでにインストールされているGPUドライバを確認する．

# マシンにインストール済みのNVIDIAドライバを一覧表示
$ dpkg -l | grep nvidia

# apt-getでインストールできるNVIDIAドライバの一覧表示
$ apt-cache search "^nvidia-[0-9]{3}$"

# NVIDIA ドライバを提供している xorg-edgers レポジトリを追加する
$ sudo add-apt-repository ppa:xorg-edgers/ppa -y
$ sudo apt-get update

# ドライバ nvidia-396 をインストール
$ sudo apt-get install -y nvidia-396
$ reboot

5.3. CUDA 10.0をマシンにインストール

• CUDA Toolkit Documentation > Release Notes > 1. CUDA Toolkit Major Components > CUDA Driver - https://docs.nvidia.com/cuda/cuda-toolkit-release-notes/index.html
• CUDA Toolkit Documentation - https://docs.nvidia.com/cuda/index.html

まず，CUDA・cuDNN・TensorFlow-GPUのバージョンを合わせる必要があります． 以下のリンクから，Tensorflow-gpuに対応するcuDNNとCUDAのバージョンを確認できます．

• https://www.tensorflow.org/install/source#linux

今回は，

• Python 3.6.9
• tensorflow-gpu 1.13.1
• CUDA 10.0
• cuDNN 7.4

で環境構築しようと思います．

以下のURLから，自分の環境にあったCUDA Toolkitパッケージをダウンロードし，マシンへインストールします．

• CUDA Toolkit Archive - https://developer.nvidia.com/cuda-toolkit-archive

注意：https://developer.nvidia.com/cuda-downloads は，最新バージョンのダウンロードリンクなので，ここから安易にダウンロードしてはいけない．特に，tensorflow-gpuは，最新のCUDA Toolkitに対応していないので注意する．CUDAとTensorflow-gpuのバージョンがあっていないと，たとえばImportError: libcublas.so.10.0が発生する． github.com

今回は，CUDA10.0で，マシンの環境として，

• Operating System: Linux
• Architecture: x86_64
• Distribution: Ubuntu
• Version: 16.04
• Installer Type: deb [network]

を選択しました．

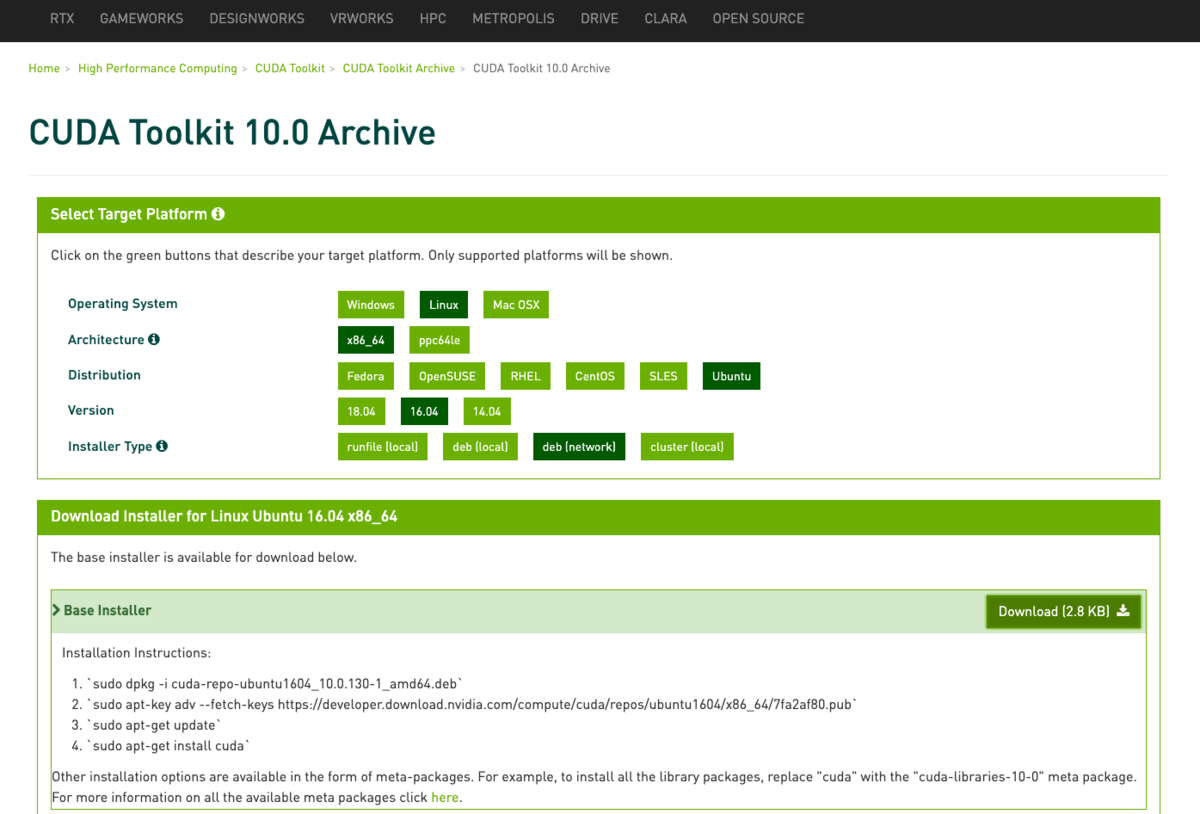
対応するCUDA Toolkit（CUDA 10.0）の.debファイル(network)は「cuda-repo-ubuntu1604_10.0.130-1_amd64.deb」です． この.debファイルをwgetコマンドを使って，マシンへダウンロードし，

$ wget https://developer.download.nvidia.com/compute/cuda/repos/ubuntu1604/x86_64/cuda-repo-ubuntu1604_10.0.130-1_amd64.deb

dpkgコマンドでパッケージとして保存します．さらに，aptコマンドでcudaパッケージをインストールします． 注意：公式に書かれているsudo apt-get install cudaを実行すると自動的に最新版のCUDAがインストールされる．

# CUDA Toolkit（CUDA 10.0）をマシンにインストールする
$ sudo dpkg -i cuda-repo-ubuntu1604_10.0.130-1_amd64.deb
$ sudo apt-key adv --fetch-keys https://developer.download.nvidia.com/compute/cuda/repos/ubuntu1604/x86_64/7fa2af80.pub
$ sudo apt-get update
$ sudo apt-get install cuda-10-0

これでCUDA Toolkit（10.0）のインストールは完了です． あとは，環境変数を設定しましょう．

• CUDAの確認

CUDA Toolkit（CUDA 10.0）が正常にインストールされているか確認します．

# CUDAがインストールされているか確認
$ ls -l /usr/local/ | grep cuda

lrwxrwxrwx 1 root root 9 11月 7 16:51 cuda -> cuda-10.0
drwxr-xr-x 16 root root 4096 11月 7 16:51 cuda-10.0

/usr/local/以下にcuda-10.0というディレクトリがあり，かつリンク cuda -> cuda-10.0が貼られています．

• CUDA Toolkit(cuda-10.0)のパス - /usr/local/cuda-10.0/bin
• NVIDIAドライバ(nvidia-418)のパス - /usr/lib/nvidia-418

次にnvccコマンドのPATHを通すために，~/.bashrcに以下を追加して，source ~/.bashrcで更新します．

# 環境変数$PATHにCUDA Toolkitのパスを追加
export PATH=/usr/local/cuda-10.0/bin:${PATH}

# 環境変数$LD_LIBRARY_PATHにCUDA Toolkitのパスを追加
export LD_LIBRARY_PATH=/usr/local/cuda-10.0/lib64:${LD_LIBRARY_PATH}

# 環境変数$LD_LIBRARY_PATHにNVIDIAドライバのパスを追加
export LD_LIBRARY_PATH=$LD_LIBRARY_PATH:/usr/lib/nvidia-418

• CUDAの詳細情報

CUDA Toolkitの詳細情報は，nvccコマンドで取得できます．

# CUDAの確認
$ nvcc -V

nvcc: NVIDIA (R) Cuda compiler driver
Copyright (c) 2005-2018 NVIDIA Corporation
Built on Sat_Aug_25_21:08:01_CDT_2018
Cuda compilation tools, release 10.0, V10.0.130

nvccコマンドは，CUDA Toolkitに対応して「/usr/local/cuda-10.1/bin/nvcc」にあればOK

$ which nvcc

/usr/local/cuda-10.0/bin/nvcc

• CUDAのバージョン確認

CUDAのバージョンを確認したい場合，/usr/local/cuda/version.txtをみればよい．

# CUDAのバージョン確認
$ cat /usr/local/cuda/version.txt

CUDA Version 10.0.130

5.4. cuDNN 7.4.2をマシンにインストール

• NVIDIA cuDNN - https://developer.nvidia.com/cudnn

• NVIDIA Deep Learning SDK Documentation - https://docs.nvidia.com/deeplearning/sdk/cudnn-install/index.html

• cuDNNのインストール

cuDNNのインストールには，NVIDIA accountを登録（無料）してログインする必要があります． （注：https://developer.nvidia.com/rdp/cudnn-download は，最新バージョンのダウンロードリンクなので，ここから安易にダウンロードしてはいけない．

• https://developer.nvidia.com/rdp/cudnn-archive

今回はCUDA10.0を使うので，「Download cuDNN v7.4.2 (Dec 14, 2018), for CUDA 10.0」を選択します．

インストールするマシンのOS（Ubuntu16.04）に合わせて，3つの.debファイルをダウンロードします．

• cuDNN Code Samples and User Guide for Ubuntu16.04 (Deb) - libcudnn7_7.4.2.24-1+cuda10.0_amd64.deb
• cuDNN Runtime Library for Ubuntu16.04 (Deb) - libcudnn7-dev_7.4.2.24-1+cuda10.0_amd64.deb
• cuDNN Developer Library for Ubuntu16.04 (Deb) - libcudnn7-doc_7.4.2.24-1+cuda10.0_amd64.deb

パッケージをダウンロードしたディレクトリで，パッケージをインストールします．

# cuDNN7.4.2 (for CUDA10.0)をインストール
$ sudo dpkg -i libcudnn7_7.4.2.24-1+cuda10.0_amd64.deb
$ sudo dpkg -i libcudnn7-dev_7.4.2.24-1+cuda10.0_amd64.deb
$ sudo dpkg -i libcudnn7-doc_7.4.2.24-1+cuda10.0_amd64.deb

注意：3つの.devファイルには依存関係があるので，「libcudnn7 > libcudnn7-dev > libcudnn7-doc」の順番でインストールする．

github.com

5.5. cuDNNの動作確認

CUDA Toolkit（CUDA10.0）に付属しているサンプルコードを実行して，cuDNNの動作確認をします．

$ cd /usr/local/cuda-10.0/bin
# ホームディレクトリにサンプルコードのあるディレクトリをコピー
$ cuda-install-samples-10.0.sh ~
Copying samples to /home/uchiumi/NVIDIA_CUDA-10.0_Samples now...
Finished copying samples.
$ cd ~/NVIDIA_CUDA-10.0_Samples
$ make
$ cd 2_Graphics/volumeRender
$ ./volumeRender # exeファイルを実行する
$ cd
$ rm -rfv ~/NVIDIA_CUDA-10.0_Samples/ # サンプルコードを消す。

5.6. cuDNNの確認

dpkg -lコマンドでインストール済みのパッケージを一覧表示する．

# マシンにインストール済みのcuDNNパッケージを一覧表示
$ dpkg -l | grep cudnn

ii libcudnn7 7.4.2.24-1+cuda10.0 amd64 cuDNN runtime libraries
ii libcudnn7-dev 7.4.2.24-1+cuda10.0 amd64 cuDNN development libraries and headers
ii libcudnn7-doc 7.4.2.24-1+cuda10.0 amd64 cuDNN documents and samples

5.7. cuDNNの保存場所

# debパッケージが保存されているディレクトリを確認(-Lオプション)
$ dpkg -L libcudnn7

/.
/usr
/usr/lib
/usr/lib/x86_64-linux-gnu
/usr/lib/x86_64-linux-gnu/libcudnn.so.7.4.2
/usr/share
/usr/share/doc
/usr/share/doc/libcudnn7
/usr/share/doc/libcudnn7/changelog.Debian.gz
/usr/share/doc/libcudnn7/copyright
/usr/share/lintian
/usr/share/lintian/overrides
/usr/share/lintian/overrides/libcudnn7
/usr/lib/x86_64-linux-gnu/libcudnn.so.7

5.9. CUDA（/usr/local/cuda-***/bin）のPATHチェック

# 出力に"/usr/local/cuda-10.0/bin"が含まれているか？
$ echo $PATH

5.10. CUDAとNVIDIAドライバ（/usr/lib/nvidia-***）のPATHチェック

# 出力に"/usr/local/cuda-10.0/lib64"と"/usr/lib/nvidia-418"が含まれているか？
$ echo $LD_LIBRARY_PATH  

5.11. CUDAとnvccコマンドのPATHチェック

# 出力が"/usr/local/cuda-10.0/bin/nvcc"になっているか？
$ which nvcc             
/usr/local/cuda-10.0/bin/nvcc

5.12. nvidia-smiコマンドのPATHチェック

# 出力が"/usr/bin/nvidia-smi"になっているか？
 $ which nvidia-smi
/usr/bin/nvidia-smi

# GPUの状態が表示されているか？
$ nvidia-smi             
Thu May 16 13:26:12 2019
+-----------------------------------------------------------------------------+
| NVIDIA-SMI 430.14       Driver Version: 430.14       CUDA Version: N/A      |
|-------------------------------+----------------------+----------------------+
| GPU  Name        Persistence-M| Bus-Id        Disp.A | Volatile Uncorr. ECC |
| Fan  Temp  Perf  Pwr:Usage/Cap|         Memory-Usage | GPU-Util  Compute M. |
|===============================+======================+======================|
|   0  GeForce GTX 1080    Off  | 00000000:01:00.0 Off |                  N/A |
| 32%   42C    P5    27W / 200W |      0MiB /  8118MiB |      0%      Default |
+-------------------------------+----------------------+----------------------+

+-----------------------------------------------------------------------------+
| Processes:                                                       GPU Memory |
|  GPU       PID   Type   Process name                             Usage      |
|=============================================================================|
|  No running processes found                                                 |
+-----------------------------------------------------------------------------+

6. Tensorflow-GPU

6.1. tensorflow インストール (1.10.0以上だとCUDAに対応していないかも)

以下のリンクから，Tensorflow-gpuに対応するcuDNNとCUDAのバージョンを確認する． - https://www.tensorflow.org/install/source#linux

なお，Version 1.16.4より最新のNumpyを使っている場合，import tensorflowとしたときに不具合が発生します． pip3 numpy install==1.16.4とすればOK．（下記参照） github.com

Ubuntuの場合，

• sudo pip3でインストールしたもの
  → /usr/local/lib/python3.?/site-packages/へ保存
• pip3でインストールしたもの
  → /home/<username>/.local/lib/python3.?/site-packages/へ保存

# tensorflow インストール
$ pip3 uninstall tensorflow-gpu
$ pip3 install tensorflow-gpu==1.13.1
$ pip3 show tensorflow-gpu # version check

pyteyon.hatenablog.com

$ python3
Python 3.6.9 (default, Jul  3 2019, 15:36:16) 
[GCC 5.4.0 20160609] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>> from tensorflow.python.client import device_lib
>>> device_lib.list_local_devices()
...

[name: "/device:CPU:0"
device_type: "CPU"
memory_limit: 268435456
locality {
}
incarnation: 12399580590058509262
, name: "/device:XLA_GPU:0"
device_type: "XLA_GPU"
memory_limit: 17179869184
locality {
}
incarnation: 8346102148670114463
physical_device_desc: "device: XLA_GPU device"
, name: "/device:XLA_CPU:0"
device_type: "XLA_CPU"
memory_limit: 17179869184
locality {
}
incarnation: 16269880268349154236
physical_device_desc: "device: XLA_CPU device"
, name: "/device:GPU:0"
device_type: "GPU"
memory_limit: 7938857370
locality {
bus_id: 1
links {
}
}
incarnation: 9065886904258284582
physical_device_desc: "device: 0, name: GeForce GTX 1080, pci bus id: 0000:01:00.0, compute capability: 6.1"
]

7.ディスプレイ

7.1 ディスプレイマネージャ(DM)を確認

$ cat /etc/X11/default-display-manager
/usr/sbin/lightdm

ja.clccomputers.com

7.2 GUI/CUIの切り替え

systemctlコマンドを使って，GUI/CUIの切り替えを行う．

#GUIログインが有効かどうか確認
$ sudo systemctl get-default
graphical.target #GUIログインが有効

# CUIログインに変更
$ sudo systemctl set-default multi-user.target 

# GUIログインに変更
$ sudo systemctl set-default graphical.target

bellsmarket.hatenablog.com

8.ディスクとファイルシステム

8.1. 現在のディレクトリ直下のファイル数を確認

lsコマンドの出力結果の行数をwcコマンドで数える．

# ファイル数を確認
$ ls -1 | wc -l

8.2. 現在のディレクトリ直下のファイルサイズを確認

ncduコマンドを使って，ファイルサイズを確認．

# ncduコマンドをインストール
$ sudo apt-get install ncdu -y (Debian/Ubuntu)
$ sudo yum install ncdu -y (RHEL系)

# ルート直下でncduコマンドを起動
$ cd /
$ ncdu

orebibou.com

duコマンドを使って，ファイルサイズを確認．duは，ディスク使用量をディレクトリごとに集計して表示するLinuxコマンド．

# カレントディレクトリ直下のファイルおよびディレクトリのディスク使用量とその合計を表示する
$ du -s -c *
84698948    Kaggle
1292748 NVIDIA_CUDA-10.1_Samples
705000  Research
107836  dataset
12  envinfo.txt
12  examples.desktop
9484    gym
7830428 workspace
1412    yt8m
686388  ダウンロード
4   テンプレート
4   デスクトップ
4   ドキュメント
4   ビデオ
4   ピクチャ
4   ミュージック
4   公開
95332296    合計

8.3. ディスクの空き領域を確認

dfコマンドを使って，ディスクの空き領域を確認．/dev/sda1が物理的な（ハードウェアレベルでの）データ容量．

# dfでディスクの空き領域を表示
# -hオプション: 読みやすいサイズ表記で表示する
$ df -h
Filesystem      Size  Used Avail Use% Mounted on
udev            7.8G     0  7.8G   0% /dev
tmpfs           1.6G  9.2M  1.6G   1% /run
/dev/sda1       214G  111G   92G  55% /
tmpfs           7.9G  184K  7.9G   1% /dev/shm
tmpfs           5.0M  4.0K  5.0M   1% /run/lock
tmpfs           7.9G     0  7.9G   0% /sys/fs/cgroup
/dev/loop0      384K  384K     0 100% /snap/patchelf/79
/dev/loop3       90M   90M     0 100% /snap/core/7713
/dev/loop2       89M   89M     0 100% /snap/core/7396
tmpfs           1.6G   36K  1.6G   1% /run/user/108
tmpfs           1.6G     0  1.6G   0% /run/user/1001
/dev/loop4      384K  384K     0 100% /snap/patchelf/87

9. Docker

9.1. Dockerをインストール

hirosanote.hatenablog.jp

9.2. Dockerチュートリアル

docs.docker.com

参考文献

• Linuxでコマンドラインからマシンスペックを確認する方法 https://qiita.com/DaisukeMiyamoto/items/98ef077ddf44b5727c29
• CUDA 9.0とcuDNN 7.0をUbuntu 16.04LTSにインストールする https://qiita.com/JeJeNeNo/items/b30597918db3781e20cf
• Ubuntu 16.04LTSにNVIDIAドライバ(nvidia-390)とCUDA 9.1を入れた時のメモ http://swytel.hatenablog.com/entry/2018/05/08/174943
• 環境構築 - Ubuntu 16.04 に NVIDIA ドライバをインストールする方法について http://pynote.hatenablog.com/entry/env-install-nvidia-driver-on-ubuntu1604

ARMA Process（自己回帰移動平均過程）

このポストでは，時系列データに対する基本的なモデル，ARMA過程についてまとめます．画像はAmazon.comの株価推移です．

経済・ファイナンスデータの計量時系列分析 (統計ライブラリー)

MA(q)過程: Moving average process

• モデル式：MA(q)

• 統計量

• 定常性

  MA(q)モデルでは統計量（）は，パラメータの値に依らず，常に定常となる．

AR(p)過程: Autoregressive process

• モデル：AR(p)

• 統計量

• 定常性

  AR(p)モデルでは統計量（）は，パラメータの値に対して，特性方程式： $$ 1 - \phi_1 {z}^1 - \cdots - \phi_p {z}^{p} = 0 $$ の複素数解の絶対値が1よりも大きい時，定常となる．

ARMA(p,q)過程: Autoregressive moving average process

• モデル：ARMA(p,q)

• 統計量

参考文献

• Autoregressive Moving Average ARMA(p, q) Models for Time Series Analysis - Part 1

経済・ファイナンスデータの計量時系列分析 (統計ライブラリー)