閃 き

閃き- blog

きらびやかに、美しく、痛烈に．

指数分布とワイブル分布をPythonでプロットしてみる

統計学 備忘


　生存時間解析など、応用範囲の広い指数分布についてまとめます。指数型分布族の仲間としては、ワイブル分布・ガンマ分布の他にも、ポアソン分布、レイリー分布、ラプラス分布（両側指数分布）などがあります。

1. 前提

1.1 確率分布の定義

　指数分布の確率密度関数 f と累積分布関数 F は、次のように定義されます。

  • 指数分布

$$ X \sim Exp(\lambda), ~~~ \lambda \geq 0 $$

$$ \begin{eqnarray} f(x | \lambda) & = & \lambda ~ exp \left( - \lambda x \right) ~~~ (x \geq 0) \\ F(x | \lambda) & = & 1 - exp \left( - \lambda x \right) ~~~ (x \geq 0) \\ \end{eqnarray} $$ $$ \begin{eqnarray} \mathbb{E}\left[ X \right] & = & \frac{1}{\lambda} \\ \mathbb{V}\left[ X \right] & = & \frac{1}{\lambda^{2}} \end{eqnarray} $$

　また、ワイブル分布は、次のように定義されます。なお、 \Gamma(~) は、ガンマ関数*1（階乗を一般化したもの）です。

  • ワイブル分布

$$ X \sim Weibull(\alpha, \beta), ~~~ \alpha \geq 0, ~~~ \beta \geq 0 $$

$$ \begin{eqnarray} f(x | \alpha, \beta) & = & \frac{\alpha}{\beta} { \left( \frac{x}{\beta} \right) }^{\alpha - 1} \left\{ - { \left( \frac{x}{\beta} \right) }^{\alpha} \right\} ~~~ (x \geq 0) \\ F(x | \alpha, \beta) & = & 1 - exp\left\{ - {\left( \frac{x}{\beta} \right) }^{a} \right\} ~~~ (x \geq 0) \\ \end{eqnarray} $$ $$ \begin{eqnarray} \mathbb{E}\left[ X \right] & = & \beta ~ \Gamma \left( 1 + \frac{1}{\alpha} \right) \\ \mathbb{V}\left[ X \right] & = & \beta^{\large \frac{2}{\alpha}} \left\{ \Gamma(1 + \frac{2}{\alpha}) - {\left( \Gamma(1 + \frac{1}{\alpha}) \right)}^{2} \right\} \end{eqnarray} $$


1. 2 指数分布とワイブル分布の関係

　ワイブル分布のパラメータをそれぞれ \alpha=1,~ \beta=\frac{1}{\lambda}とすると指数分布に一致します。つまり、ワイブル分布は、指数分布の一般に拡張したものになります。

$$ Exp(\lambda) = Weibull(1, \frac{1}{\lambda}) $$

ちなみに、以下で定義されるガンマ分布のパラメータをそれぞれ \alpha=1,~ \beta=\frac{1}{\lambda}とすると指数分布に一致します。

$$ Exp(\lambda) = Weibull(1, \frac{1}{\lambda}) = Gamma(1, \frac{1}{\lambda}) $$

  • ガンマ分布

$$ X \sim Gamma(\alpha, \beta) $$

$$ \begin{eqnarray} f(x | \alpha, \beta) & = & \frac{1}{\Gamma(\alpha)} \frac{1}{\beta} {\left( \frac{x}{\beta} \right) }^{\alpha - 1}~~~ (x \gt 0) \\ \end{eqnarray} $$ $$ \begin{eqnarray} \mathbb{E}\left[ X \right] & = & \alpha \beta \\ \mathbb{V}\left[ X \right] & = & \alpha {\beta}^{2} \end{eqnarray} $$


2. Pythonによる実装

2.1 指数分布

python で分布を定義して、グラフをプロットしてみます。

import math
import random
import numpy as np
import matplotlib.pyplot as plt

# 指数分布

class Exp():
    def __init__(self):
        pass
    
    # 密度関数f
    def f(self, x, la=1):
        return la * math.exp(-1 * la * x)
    
    # 分布関数F
    def F(self, x, la=1):
        return 1 - math.exp(-1 * la * x)
    
    # Fの逆関数(samplingに使う)
    def invF(self, y, la=1):
        return -1 * (1 / la) * math.log(1 - y)
    
    # サンプリング
    def sampling(self, num, la):
        sample=[]
        for i in range(num):
            rand = random.random()
            sample.append(self.invF(rand, la))
        return np.array(sample)
    
    # 散布図
    def scatter_pdf(self, ax, data, la, alpha=0.4):
        pdf=[]
        for d in data:
            pdf.append(self.f(d, la))

        ax.scatter(data, pdf, alpha=alpha)
        ax.set_title("Exponential (lambda={:.2f})".format(la))
        ax.set_xlabel("value")
        ax.set_ylabel("probability density")
        ax.set_ylim(0, 1)
        
    # グラフ
    def plot_pdf(self, ax, data, la):
        pdf=[]
        for d in data:
            pdf.append(self.f(d, la))

        ax.plot(data, pdf)
        ax.set_title("Exponential (lambda={:.2f})".format(la))
        ax.set_xlabel("value")
        ax.set_ylabel("probability density")
        ax.set_ylim(0, 1)

実際にグラフを描画してみます。パラメータ \lambda の値を変えて、分布の形状をみます。

# グラフをmatplotlibで描画してみる

data = np.linspace(0, 15, 100)

fig, ax = plt.subplots(3, 3, figsize=(18, 18))

Exp().plot_pdf(ax[0, 0], data, 0.2)
Exp().plot_pdf(ax[0, 1], data, 0.4)
Exp().plot_pdf(ax[0, 2], data, 0.6)
Exp().plot_pdf(ax[1, 0], data, 0.8)
Exp().plot_pdf(ax[1, 1], data, 1)
Exp().plot_pdf(ax[1, 2], data, 1.2)
Exp().plot_pdf(ax[2, 0], data, 1.4)
Exp().plot_pdf(ax[2, 1], data, 1.6)
Exp().plot_pdf(ax[2, 2], data, 1.8)

plt.show()
f:id:yumaloop:20190114000052p:plain:w1000

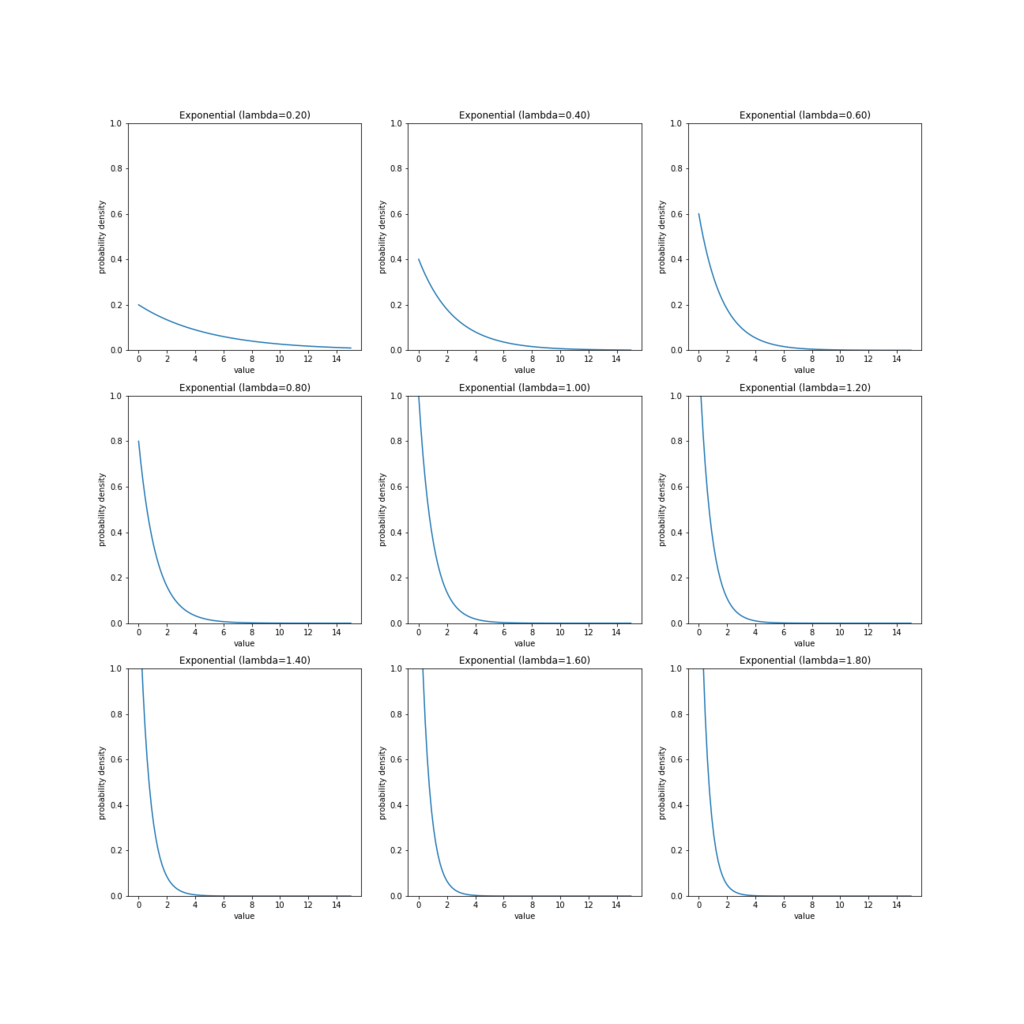
　プロットをみると、指数分布のパラメータ \lambda は、尺度（ばらつき）を表していることがわかります。分布は \lambda が大きくなるにつれ急峻になり、ばらつきが少なくなっていきます。平均について \frac{1}{\lambda} \to 0 ~ (\lambda \to \infty)、分散について \frac{1}{\lambda^{2}} \to 0 ~ (\lambda \to \infty) となることから、「指数分布はパラメータ \lambda を上げると、平均は０に接近し、分散は限りなく小さくなる（０になる）」ということがわかります。

2.2 ワイブル分布

python で分布を定義して、グラフをプロットしてみます。

import math
import random
import numpy as np
import matplotlib.pyplot as plt

# ワイブル分布

class Weibull():
    def __init__(self):
        pass
        
    # 密度関数f
    def f(self, x, a, b):
        return (a/b) * ( (x/b)**(a - 1) ) * math.exp(-1 * (x/b)**a )
    
    # 分布関数F
    def F(self, x, a, b):
        return 1 - math.exp(-1 * (x/b)**a )
    
    # Fの逆関数
    def invF(self, y, a, b):
        return b * ( -1 * math.log(1 - y) )**(1/a)
    
    # サンプリング
    def sampling(self, num, a, b):
        sample=[]
        for i in range(num):
            rand = random.random()
            sample.append(self.invF(rand, a, b))
        return np.array(sample)
    
    # 散布図
    def scatter_pdf(self, ax, data, a, b, alpha=0.4):
        pdf=[]
        for d in data:
            pdf.append(self.f(d, a, b))

        ax.scatter(data, pdf, alpha=alpha)
        ax.set_title("Weibull (alpha={:.2f}, beta={:.2f})".format(a, b))
        ax.set_xlabel("value")
        ax.set_ylabel("probability density")
        ax.set_ylim(0, 1)
        
    # グラフ
    def plot_pdf(self, ax, data, a, b):
        pdf=[]
        for d in data:
            pdf.append(self.f(d, a, b))

        ax.plot(data, pdf)
        ax.set_title("Weibull (alpha={:.2f}, beta={:.2f})".format(a, b))
        ax.set_xlabel("value")
        ax.set_ylabel("probability density")
        ax.set_ylim(0, 1)

実際にグラフを描画してみます。パラメータ \alpha, ~\beta の値を変えて、分布の形状をみます。

# グラフをmatplotlibで描画してみる

data = np.linspace(0, 15, 100)

fig, ax = plt.subplots(3, 3, figsize=(18, 18))

Weibull().plot_pdf(ax[0, 0], data, 1, 1)
Weibull().plot_pdf(ax[0, 1], data, 1, 2)
Weibull().plot_pdf(ax[0, 2], data, 1, 3)
Weibull().plot_pdf(ax[1, 0], data, 2, 1)
Weibull().plot_pdf(ax[1, 1], data, 2, 2)
Weibull().plot_pdf(ax[1, 2], data, 2, 3)
Weibull().plot_pdf(ax[2, 0], data, 3, 1)
Weibull().plot_pdf(ax[2, 1], data, 3, 2)
Weibull().plot_pdf(ax[2, 2], data, 3, 3)

plt.show()
f:id:yumaloop:20190114000114p:plain:w1000

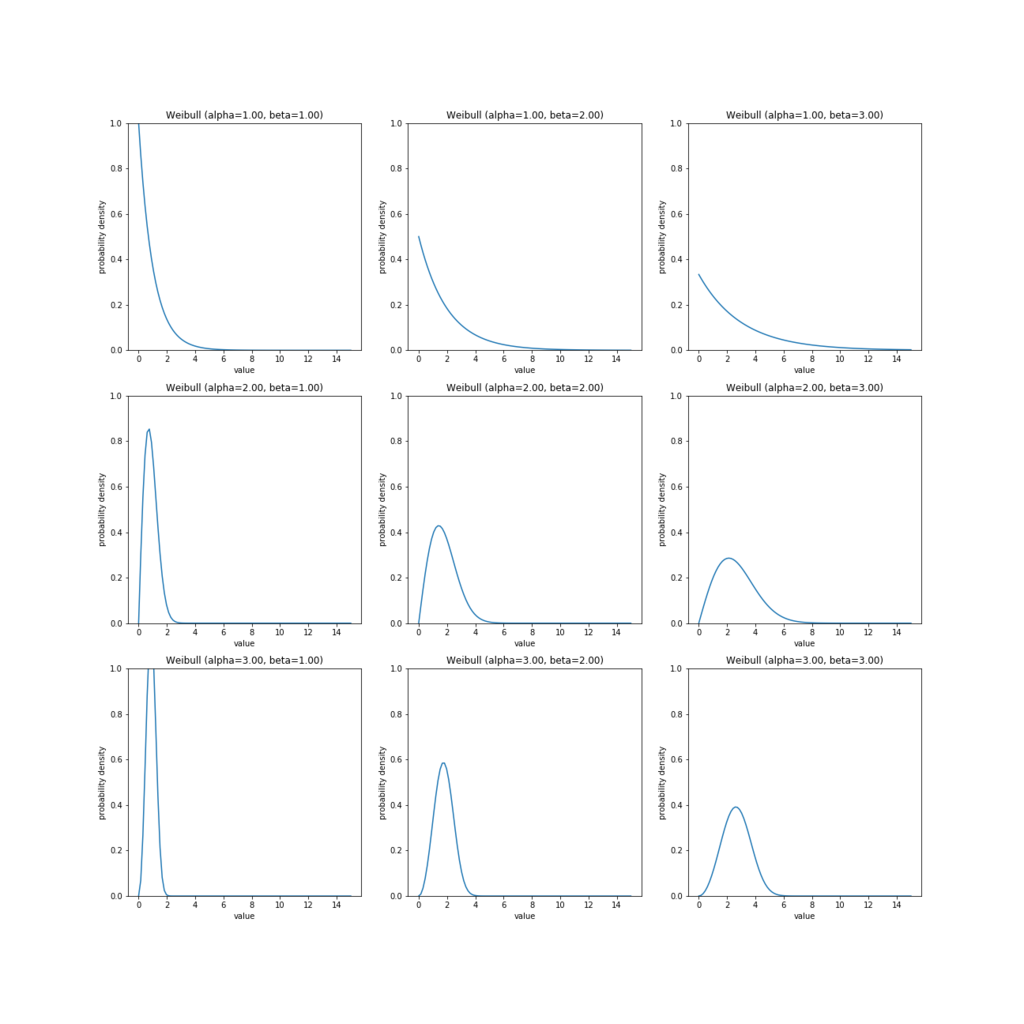
　プロットをみると、ワイブル分布のパラメータ \alpha は分布の形状を表し、パラメータ \beta は、尺度（ばらつき）を表していることがわかります。実際、分布の形状は \alpha によって支配されており、ワイブル分布は \alpha=1 のとき指数分布、 \alpha=2 のときレイリー分布と一致します。分布は \beta が大きくなるにつれ急峻になり、ばらつきが少なくなっていきます。

*1:ガンマ関数は、$$ \Gamma(n):=\int_{0}^{\infty} y^{n - 1} e^{-y} dy $$と定義され、 n が自然数ならば \Gamma(n)=(n-1)! が成り立つ。