最尤推定量とワルド検定・スコア検定・尤度比検定

1. パラメータの尤もらしさに関する統計的仮説検定

　何らかのパラメトリックな確率モデル とコのデータサンプル（標本） に対して定義される対数尤度関数 を用いて、「あるパラメータ が最尤推定量 と一致しているかどうか」に真偽を与える統計的仮説検定を考えます。すなわち、仮説：

・帰無仮説
・対立仮説

を設けて、帰無仮説 を有意水準 で棄却する条件を、データ（標本）に基づく統計量とその分布から求めます。

　このポストでは、上記の検定方式として、Wald検定・Score検定・尤度比検定の3つを紹介します。これらは、パラメータ空間 から への写像である対数尤度関数 を中心に考えると、自然な導出であることがわかります。（下図参照）

1.1 ワルド検定（Wald test）

ワルド検定では、現在のパラメータ と最尤推定量 との差を基に検定を行います。

最尤推定量 に対するワルド検定（Wald test）

最尤推定量の漸近正規性（Asymptotic normality）：

が成り立つとき、仮説：

・帰無仮説
・対立仮説

における帰無仮説 の有意水準 の棄却域 は、

で与えられる。

1.2 スコア検定（Score test）

スコア検定では、現在のパラメータ の対数尤度関数における傾き（スコア関数）を基に検定を行います。

最尤推定量 に対するスコア検定（Score test）

スコア関数 とフィッシャー情報量 の定義

より、スコア関数 の平均と分散が

であることから、中心極限定理（CLT, Central Limit Theorem）を用いて、

が成り立つ。よって、仮説：

・帰無仮説
・対立仮説

における帰無仮説 の有意水準 の棄却域 は、

で与えられる。

1.3 尤度比検定（Likelihood ratio test）

尤度比検定では、現在のパラメータ の対数尤度と最尤推定量 との対数尤度の差を基に検定を行います。

最尤推定量 に対する尤度比検定（Likelihood ratio test）

尤度比検定統計量 を

と定義すると、仮説：

・帰無仮説
・対立仮説

において、帰無仮説 の下で、

が成り立つことから、帰無仮説 の有意水準 の棄却域 は、

で与えられる。

2. KL-divergenceとFischer情報量の関係

2.1 スコア関数とFischer情報量の定義

　スコア関数 を以下のように定義します．

対数関数の微分に注意すると，スコア関数 の期待値は0になります．

さらに，スコア関数の分散は，Fischer情報量 といい，以下のように計算されます．

パラメータ がn次元の場合，スコア関数は を用いて定義されるn次元ベクトル，Fischer情報量 は 行列となります．

2.2 KL-divergence

ここで、パラメータ の尤度 と、パラメータ の値を微小量 だけ変化させたときの尤度 との乖離度として、KL-divergenceを考えます。

さらに、 を の関数とみて、 のまわりでテイラー展開（マクローリン展開）をすると、

となります。よって、パラメータ の微小変化に対する KL-divergence：

の局所二次近似は、

となります。すなわち、パラメータ のFischer情報量は、パラメータ の微小変化に対する KL-divergenceと密接に関連した量であることがわかります。以上の結果は、次の定理にまとめられます。

の対数尤度関数 に基づいて導かれる検定および統計量をまとめると下図のようになります。

　最尤推定は、さまざまな確率モデルに対する最適化（学習）の基本であり、尤度関数（損失関数）の挙動を正確に把握することがとても重要です。Deep learningなど、高次元のパラメータ空間をもつ確率モデルの場合でも、二次の偏導関数（ヘッセ行列）によって、尤度関数の凸性・曲率が全て記述*1され、これはパラメータに対するFischer情報量行列と密に関連します。すなわち、Fischer情報量行列が正則行列でない*2場合、尤度関数はパラメータに対して非凸で複雑な関数となり、最尤推定量を探索することはより難しくなります。

Fischer情報量行列の定義やhessianとの関連については，以下のブログ記事が参考になります．

wiseodd.github.io

3. 参考書籍

新装改訂版 現代数理統計学

現代数理統計学の基礎 (共立講座 数学の魅力)

Statistics

*1:線形空間では基底ベクトルに対する微分さえわかれば、あらゆる方向に対する勾配がその線形結合として表現可能です。

*2:すべての固有値が正である行列のことを、正則行列といいます。これに対し，正則行列ではない行列を特異行列ということがあります。

ガウス過程と回帰モデル（線形~線形基底~ガウス過程）

※ このポストの内容は、PRML下巻6章とGPML2章を参考にしています。

www.microsoft.com www.gaussianprocess.org

1. ガウス過程（GP, Gaussian Process）

1.1 ガウス分布の共役性

　任意の確率モデル に対して の事前分布 としてガウス分布を仮定した場合、ベイズの定理によって求められる の事後分布 もガウス分布に従います。つまり、ガウス分布に従うパラメータ について、任意の確率モデル とデータサンプル から、事後分布 を求める操作はガウス分布の中で閉じています。一般に、「事前分布としてある確率分布を仮定すると、事後分布も同じ確率分布に従う」という性質を共役性といい、ガウス分布は共役性をもちます。

$$ \begin{eqnarray} (Posterior~of~w) & = & \frac{(likelihood ~of~ X^{n})\times(Prior~of~w)}{(Evidence~of~the~model)} \\ \\ p(w|X^{n}) & = & \frac{p(X^{n}|w)p(w)}{\int p(X^{n}|w)p(w) ~dw} \end{eqnarray} $$ $$ p(w) \sim N(\mu, s) ~ \Rightarrow ~ p(w|X^{n}) \sim N(\mu', s') $$

1.2 ガウス分布の切断と周辺化

　それぞれがガウス分布に従う「互いに独立でない」確率変数列 を考えます。このとき、確率変数列 はNコの確率変数 のペアであるため、確率変数列 そのものを 次元の確率変数として扱うことができます。同様に、確率変数列 における「任意の コの部分列」は 次元の確率変数として扱えます。

　平均が で、共分散行列が のN次元ガウス分布に従う確率変数 ：

に対して、（）による分割を考えます。

このとき、 は以下のようなガウス分布に従います。

さらに、「 の共分散行列 は半正定値対称行列である」ことから、次式が成り立ちます。

ここで、「 は独立ではない」ことに注意すると、条件つき確率 は次のように与えられ、条件つき平均 と条件つき共分散行列 からなるガウス分布に従うことがわかります。

を手元にあるデータサンプル、 を新しいデータサンプルと捉えると、これらを結合した に対してガウス過程を導入することができます。

1.3 ガウス過程の定義

　任意の組が同時ガウス分布（joint Gaussian distribution）に従うような確率変数の集合 を，ガウス過程（Gaussian Process, GP）と定義します。ガウス分布とガウス過程を比較すると以下のようになります。

• ガウス分布（Gaussian distribution）
  • 任意のガウス分布 は、平均 と共分散行列 によって完全に記述される。

• ガウス過程（Gaussian Process, GP）
  • 任意のガウス過程 は、平均関数 と共分散関数 によって完全に記述される。

2. さまざまな回帰モデルの比較

2.1 回帰問題とは？

　まず、回帰（Regression）に一般的な定義を与えてみます。

　確率変数 の実現値からなるNコのデータサンプル：

$$ \mathcal{D} := \left\{ \left( \begin{array}{c} {\bf x}_1 \\ y_1 \end{array} \right), \dots, \left( \begin{array}{c} {\bf x}_N \\ y_N \end{array} \right) \right\} $$

を用いて、 の値から の値を推定（予測）するモデル：

$$ f: X \in \mathbb{R}^{d} \to Y \in \mathbb{R} $$

を作りたい。

ここで、モデル による推定値 と真値 との推定誤差 を次のように定義し、

$$ \varepsilon_i := y_i - f({\bf x}_i) ~~~ (i=1, \dots, N) $$

さらに、各 はそれぞれ独立に同じパラメータをもつガウス分布に従うと仮定すると、

$$ y_i = f({\bf x}_i) + {\varepsilon}_i ~~~ (i=1, \dots N) \\ {\varepsilon}_i \sim N \left( 0, \frac{1}{\beta} \right) $$

という等式が得られます。これをまとめると、

$$ p( y_i | {\bf x}_i, f) = N \left( f({\bf x}_i), \frac{1}{\beta} \right) $$

となり、回帰問題の目的を、「を定めることで，任意のに対する条件付き確率 を定めること」とベイズ的に解釈することも可能です。すなわち、次式（ベイズの定理）で、 はデータサンプル への「当てはまりの良さ（=尤度）」を表しますが、同時に、 によって、データサンプル から の事後確率と予測分布が決定されます。

$$ p( f | y_i, {\bf x}_i ) = \frac{ p( y_i | {\bf x}_i, f ) p(f) } {p( y_i | {\bf x}_i )} $$

　一般化に、回帰問題では、データサンプル とモデル に対して

$$ p( f | {\bf y}, {\bf X} ) = \frac{ p( {\bf y} | {\bf X}, f ) p(f) } {p( {\bf y} | {\bf X} )}, ~~ i.e. ~~ p( f | \mathcal{D} ) = \frac{ p( \mathcal{D} | f ) p(f) } {p( \mathcal{D} )} $$

という構造が現れます。次章以降で、具体的な回帰モデルについて、解説したいと思います。

2.2 線形回帰モデル

2.2.1 線形回帰モデルの準備

　もっとも　素朴な回帰モデルとして「線形回帰モデル」を考えます。モデルパラメータとして、重みベクトル を想定します。

$$ y_i = f({\bf x}_i) + \varepsilon_i, \\ f({\bf x}_i) = {\bf x}_i^{\rm T} {\bf w} = \left( \begin{array}{c} x_{i1}, \dots, x_{id} \end{array} \right) \cdot \left( \begin{array}{c} w_{1} \\ \vdots \\ w_{d} \end{array} \right), ~~~ \varepsilon_i \sim N \left( 0, \frac{1}{\beta} \right) $$

これらの関係式をまとめると、各 に対する の推定値は、次式のように「ばらつきを持った確率モデル」として表現されます。

$$ p( y_i | x_i, {\bf w} ) = N \left( y_i | f({\bf x}_i), \frac{1}{\beta}{\bf I} \right) = N \left( {\bf x}_i^{\rm T} {\bf w}, \frac{1}{\beta} \right) $$

さらに、個々データではなくデータセット 全体に対して、回帰モデル はどのように作用するのかをまとめて考えます。計画行列（design matrix） と、ベクトル を以下のように定義します。

$$ {\bf X} := \left( {\bf x}_1, {\bf x}_2, \dots, {\bf x}_N \right)= \left( \begin{array}{cccc} x_{11} & x_{21} & \dots & x_{N1}\\ x_{12} & x_{22} & \dots & x_{N2}\\ \vdots & \vdots & \dots & \vdots \\ x_{1N} & x_{2N} & \dots & x_{NN} \end{array} \right), ~~~ {\bf y} := \left( \begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_N \end{array} \right), ~~~ {\boldsymbol \varepsilon} := \left( \begin{array}{c} \varepsilon_1 \\ \varepsilon_2 \\ \vdots \\ \varepsilon_N \end{array} \right) $$

すると、「線形回帰モデル」は以下のように記述され、

$$ {\bf y} = f({\bf X}) + {\boldsymbol \varepsilon}, \\ f({\bf X}) = {\bf X}^{\rm T}{\bf w}, ~~~ \boldsymbol \varepsilon \sim N \left( {\bf 0}, \frac{1}{\beta}{\bf I}\right) $$

これらの関係式をまとめると、 データセット における の推定値は、次式のように「ばらつきを持った確率モデル」として表現されます。

$$ p( {\bf y} | {\bf X}, {\bf w} ) = N \left( {\bf y} | f({\bf X}), \frac{1}{\beta}{\bf I} \right) = N \left( {\bf X}^{\rm T} {\bf w}, \frac{1}{\beta}{\bf I} \right) $$

2.2.2 線形回帰モデルのベイズ的解釈

　線形回帰モデルにおいて、 を推定する確率モデル の性能はパラメータ の値によって左右されます。確率モデル をベイズの枠組み:

$$ p({\bf w} | {\bf y}, {\bf X} ) = \frac{ p({\bf y} | {\bf X}, {\bf w}) p({\bf w}) } {p({\bf y} | {\bf X} )} = \frac{ p({\bf y} | {\bf X}, {\bf w}) p({\bf w}) } { \int p({\bf y} | {\bf X}, {\bf w}) p({\bf w}) ~ d{\bf w}} $$

によって拡張し、パラメータ の事後分布 を導出することで、N+1 番目の未知のデータサンプル に対する「ばらつきを持った確率モデル」である予測分布を導出しましょう。

（１） の事前分布

$$ p({\bf w}) = N \left( {\bf w} ~ | ~ {\bf 0}, ~ \frac{1}{\alpha} {\bf I} \right) $$

（２）尤度

$$ \begin{eqnarray} p({\bf y} | X, {\bf w}) & = &\prod_{i=1}^{N} p(y_i | {\bf x}_i, {\bf w}) \\ & = & \prod_{i=1}^{N} \frac{1}{ \sqrt{ 2 \pi \beta^{-1}}} \exp \left( - \frac{{\left( y_i - {{\bf x}_i}^{\rm T}{\bf w} \right)}^{2}}{2 \beta^{-1}} \right) \\ & = & \frac{1}{ {\left( 2 \pi \beta^{-1} \right)}^{n/2}} \exp \left( - \frac{{\left( {\bf y} - X^{\rm T}{\bf w} \right)}^{2}}{2 \beta^{-1}} \right) \\ & = & N \left( {\bf y} ~ | ~ X^{\rm T}{\bf w}, ~ \frac{1}{\beta}{\bf I} \right) \end{eqnarray} $$

（３） の事後分布

$$ \begin{eqnarray} p({\bf w} | {\bf X}, {\bf y}) & \propto & \exp \left( - \frac{1}{2} { ( {\bf y} - {\bf X}^{\rm T}{\bf w} ) }^{\rm T} { \left( \frac{1}{\beta} {\bf I} \right) }^{-1} ( {\bf y} - {\bf X}^{\rm T}{\bf w} ) \right) \exp \left( - \frac{1}{2} {\bf w}^{\rm T} { \left( \frac{1}{\alpha} {\bf I} \right) }^{-1} {\bf w} \right) \\ & \propto & \exp \left( { ( {\bf w} - {\hat{\bf w}}_{MAP} ) }^{\rm T} \left( \beta {\bf X}{\bf X}^{\rm T} + \alpha {\bf I} \right) ( {\bf w} - {\hat{\bf w}}_{MAP} ) \right) \\ & = & N \left( {\bf w} ~ | ~ {\hat{\bf w}}_{MAP}, ~ {\bf A}^{-1} \right) \end{eqnarray} $$

　ただし、

$$ \begin{eqnarray} {\hat{\bf w}}_{MAP} & := & \beta {\bf A }^{-1} {\bf X}{\bf y} \\ {\bf A} & := & \beta {\bf X}{\bf X}^{\rm T} + \alpha {\bf I} \end{eqnarray} $$

（４） の予測分布

$$ \begin{eqnarray} p^{*}(y^{*} | {\bf x}^{*}, {\bf X}, {\bf y}) & = & \int p(y^{*} | {\bf x}^{*}, {\bf w}) p( {\bf w} | X, {\bf y}) ~ d{\bf w} \\ & = & N \left( y^{*} ~|~ \beta {{\bf x}^{*}}^{\rm T} { \bf A }^{-1} {\bf X} {\bf y}, ~ { {\bf x}^{*}}^{\rm T} { \bf A }^{-1} {\bf x}^{*} \right) \end{eqnarray} $$

2.3 線形基底モデル

2.3.1 線形基底モデルの準備

　素朴な線形回帰モデルでは，入力ベクトル のあるデータ空間（data space） の中で，出力 を推定します．しかし，この場合，データ空間を構成する基底ベクトルの線形結合によって を推定するため, モデルの表現力が制約されてします。そこで，入力ベクトル を，基底関数（basis function） によって特徴量 へと変換し，高次元の特徴空間 （feature space）から の値を推定することを考えます．ここで，基底関数 による変換は線形でも非線形でもよいとします．

$$ {\bf x}_i \in \mathbb{R}^d \to \phi({\bf x}_i) \in \mathbb{R}^M \underset{\large \bf w}{\longrightarrow} f({\bf x}_i) \in \mathbb{R} \underset{ {\large \varepsilon_i} } {\longleftrightarrow} y_i \in \mathbb{R}, ~~~ (i=1, \dots, N) \\ $$

基底関数 は、データを表現する基底を変える（空間を変える）関数と考えることができます。また、一般に、 であることから、 はデータサンプルを高次元空間に写像する（mapping）関数であることがわかります。

• のデータ空間 における表現： $$ {\bf x}_i = \left( x_{i1}, x_{i2}, \dots, x_{id} \right) $$
• の特徴空間 における表現： $$ \phi({\bf x}_i) = \left( \phi_{1}({\bf x}_i), \phi_{2}({\bf x}_i), \dots, \phi_{M}({\bf x}_i) \right) $$

実際に，「線形基底モデル」を構築しましょう．モデルパラメータとして，重みベクトル を想定します．

$$ y_i = f({\bf x}_i) + \varepsilon_i \\ f({\bf x}_i) = { \phi ( {\bf x}_i ) }^{\rm T} {\bf w} = \left( \begin{array}{c} \phi_{1}({\bf x}_i), \dots, \phi_{M}({\bf x}_i) \end{array} \right) \cdot \left( \begin{array}{c} w_{1} \\ \vdots \\ w_{M} \end{array} \right), ~~~ \varepsilon_i \sim N \left( 0, \frac{1}{\beta} \right) $$

これらの関係式をまとめると、各 に対する の推定値は、次式のように「ばらつきを持った確率モデル」として表現されます。

$$ p( y_i | x_i, {\bf w} ) = N \left( y_i | f( {\bf x}_i ), \frac{1}{\beta} \right) = N \left( y_i | {\phi ( {\bf x}_i ) }^{\rm T} {\bf w}, \frac{1}{\beta} \right) $$

さらに、個々データではなくデータセット 全体に対して、回帰モデル はどのように作用するのかをまとめて考えます。計画行列（design matrix） と、ベクトル を以下のように定義します。

$$ \Phi({\bf X}) := \left( \phi({\bf x}_1), \phi({\bf x}_2), \dots, \phi({\bf x}_N) \right)= \left( \begin{array}{cccc} \phi_{1}({\bf x}_1) & \phi_{1}({\bf x}_2) & \dots & \phi_{1}({\bf x}_N) \\ \phi_{2}({\bf x}_1) & \phi_{2}({\bf x}_2) & \dots & \phi_{2}({\bf x}_N) \\ \vdots & \vdots & \dots & \vdots \\ \phi_{M}({\bf x}_1) & \phi_{M}({\bf x}_2) & \dots & \phi_{M}({\bf x}_N) \end{array} \right), ~~~ {\bf y} := \left( \begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_N \end{array} \right), ~~~ {\boldsymbol \varepsilon} := \left( \begin{array}{c} \varepsilon_1 \\ \varepsilon_2 \\ \vdots \\ \varepsilon_N \end{array} \right) $$

すると、「線形基底回帰モデル」は以下のように記述され、

$$ {\bf y} = f({\bf X}) + {\boldsymbol \varepsilon}, \\ f({\bf X}) = {\Phi({\bf X})}^{\rm T}{\bf w}, ~~~ \boldsymbol \varepsilon \sim N \left( {\bf 0}, \frac{1}{\beta}{\bf I}\right) $$

これらの関係式をまとめると、 データセット における の推定値は、次式のように「ばらつきを持った確率モデル」として表現されます。

$$ p( {\bf y} | {\bf X}, {\bf w} ) = N \left( {\bf y} ~|~ f({\bf X}), \frac{1}{\beta}{\bf I} \right) = N \left( {\bf y} ~|~ {\Phi({\bf X})}^{\rm T}{\bf w}, \frac{1}{\beta}{\bf I} \right) $$

2.3.2 線形基底モデルのベイズ的解釈

　確率モデル をベイズの枠組み:

$$ p({\bf w} | {\bf y}, {\bf X} ) = \frac{ p({\bf y} | {\bf X}, {\bf w}) p({\bf w}) } {p({\bf y} | {\bf X} )} = \frac{ p({\bf y} | {\bf X}, {\bf w}) p({\bf w}) } { \int p({\bf y} | {\bf X}, {\bf w}) p({\bf w}) ~ d{\bf w}} $$

によって拡張し、パラメータ の事後分布 を導出することで、N+1 番目の未知のデータサンプル に対する「ばらつきを持った確率モデル」である予測分布を導出しましょう。

（１） の事前分布

$$ p({\bf w}) = N \left( {\bf w} ~ | ~ {\bf 0}, ~ \frac{1}{\alpha} {\bf I} \right) $$

（２）尤度

$$ \begin{eqnarray} p({\bf y} | \Phi({\bf X}), {\bf w}) & = &\prod_{i=1}^{N} p(y_i | \phi({\bf x}_i), {\bf w}) \\ & = & \prod_{i=1}^{N} \frac{1}{ \sqrt{ 2 \pi \beta^{-1}}} \exp \left( - \frac{{\left( y_i - {\phi({\bf x}_i)}^{\rm T}{\bf w} \right)}^{2}}{2 \beta^{-1}} \right) \\ & = & \frac{1}{ {\left( 2 \pi \beta^{-1} \right)}^{n/2}} \exp \left( - \frac{{\left( {\bf y} - {\Phi({\bf X})}^{\rm T}{\bf w} \right)}^{2}}{2 \beta^{-1}} \right) \\ & = & N \left( {\bf y} ~ | ~ {\Phi({\bf X})}^{\rm T}{\bf w}, ~ \frac{1}{\beta}{\bf I} \right) \end{eqnarray} $$

（３） の事後分布

$$ \begin{eqnarray} p({\bf w} | \Phi({\bf X}), {\bf y}) & \propto & \exp \left( - \frac{1}{2} { ( {\bf y} - {\Phi({\bf X})}^{\rm T}{\bf w} ) }^{\rm T} { \left( \frac{1}{\beta} {\bf I} \right) }^{-1} ( {\bf y} - {\Phi({\bf X})}^{\rm T}{\bf w} ) \right) \exp \left( - \frac{1}{2} {\bf w}^{\rm T} { \left( \frac{1}{\alpha} {\bf I} \right) }^{-1} {\bf w} \right) \\ & \propto & \exp \left( { ( {\bf w} - {\hat{\bf w}}_{MAP} ) }^{\rm T} \left( \beta {\Phi({\bf X})}{\Phi({\bf X})}^{\rm T} + \alpha {\bf I} \right) ( {\bf w} - {\hat{\bf w}}_{MAP} ) \right) \\ & = & N \left( {\bf w} ~ | ~ {\hat{\bf w}}_{MAP}, ~ { A }^{-1} \right) \end{eqnarray} $$

　ただし、

$$ \begin{eqnarray} {\hat{\bf w}}_{MAP} & := & \beta { \bf A }^{-1} {\bf X}{\bf y} \\ A & := & \beta {\Phi({\bf X})}{\Phi({\bf X})}^{\rm T} + \alpha {\bf I} \end{eqnarray} $$

（４） の予測分布

$$ \begin{eqnarray} p^{*}(y^{*} | {\bf x}^{*}, \Phi({\bf X}), {\bf y}) & = & \int p(y^{*} | {\bf x}^{*}, {\bf w}) p( {\bf w} | \Phi({\bf X}), {\bf y}) ~ d{\bf w} \\ & = & N \left( y^{*} ~|~ \beta {{\bf x}^{*}}^{\rm T} { \bf A}^{-1} \Phi({\bf X}) {\bf y}, ~ { {\bf x}^{*}}^{\rm T} { \bf A}^{-1} {\bf x}^{*} \right) \end{eqnarray} $$

2.4 ガウス過程による線形基底モデルの表現

2.4.1 ガウス過程による回帰モデルの準備

　ガウス過程による回帰では、基底関数 ではなく、回帰モデル の確率分布 の共分散行列 を事前に定めます。 をグラム行列（Gram Matrix）といいます。

$$ {\bf K}_{XX} = \left( \begin{array}{cccc} k({\bf x}_1, {\bf x}_1) & k({\bf x}_1, {\bf x}_2) & \dots & k({\bf x}_1, {\bf x}_N) \\ k({\bf x}_2, {\bf x}_1) & k({\bf x}_2, {\bf x}_2) & \dots & k({\bf x}_2, {\bf x}_N) \\ \vdots & \vdots & \ddots & \vdots \\ k({\bf x}_N, {\bf x}_1) & k({\bf x}_N, {\bf x}_2) & \dots & k({\bf x}_N, {\bf x}_N) \\ \end{array} \right) $$ ただし、 $$ \begin{eqnarray} k({\bf x}_i, {\bf x}_j) & = & C o v \left[ f( {\bf x}_i ), f( {\bf x}_j ) \right] \\ & = & { \phi( {\bf x}_i )}^{\rm T} \left( \frac{1}{\alpha} {\bf I} \right) \phi( {\bf x}_j ) \\ & = & \frac{1}{\alpha} \phi_{1}( {\bf x}_i ) \phi_{1}( {\bf x}_j ) + \cdots + \frac{1}{\alpha} \phi_{M}( {\bf x}_i ) \phi_{M}( {\bf x}_j ) \end{eqnarray} $$

　定義から、グラム行列 は と の分散からなる行列（=共分散行列）です。すなわち、グラム行列 は、基底関数（basis function） と計画行列（design matrix） および重みベクトル の事前分布 によっても記述されます。

$$ \begin{eqnarray} {\bf K}_{XX} & = & \left( \begin{array}{cccc} C o v \left[ f({\bf x}_1), f({\bf x}_1) \right] & C o v \left[ f({\bf x}_1), f({\bf x}_2) \right] & \dots & C o v \left[ f({\bf x}_1), f({\bf x}_N) \right] \\ C o v \left[ f({\bf x}_2), f({\bf x}_1) \right] & C o v \left[ f({\bf x}_2), f({\bf x}_2) \right] & \dots & C o v \left[ f({\bf x}_2), f({\bf x}_N) \right] \\ \vdots & \vdots & \ddots & \vdots \\ C o v \left[ f({\bf x}_N), f({\bf x}_1) \right] & C o v \left[ f({\bf x}_N), f({\bf x}_2) \right] & \dots & C o v \left[ f({\bf x}_N), f({\bf x}_N) \right] \\ \end{array} \right) \\ \\ & = & {\Phi({\bf X})}^{\rm T} \left( \frac{1}{\alpha}{\bf I} \right) \Phi({\bf X}) \\ & = & \frac{1}{\alpha} \Phi({\bf X}) { \Phi({\bf X}) }^{\rm T} \end{eqnarray} $$

すなわち、同一の線形基底モデルは，以下の2つの視点から記述することが可能です．ガウス過程を含む「カーネル法」は，後者の関数空間による視点（function space view）に根ざした多変量解析手法です．

1. 基底関数 と計画行列 によって表現する（weight space view）
   • モデル設計者は，基底関数 を事前に定める．
2. グラム行列 によって表現する（function space view）
   • モデル設計者は，カーネル関数 を事前に定める．

以上より，モデルの出力値 と変数 の確率分布は，次のように導出されます，

$$ \begin{eqnarray} p \bigl( f({\bf X}) \bigr) & = & N \left( f({\bf X}) ~|~ {\bf 0}, \frac{1}{\alpha}\Phi({\bf X}) {\Phi({\bf X})}^{\rm T} \right) \\ & = & N \Bigl( f({\bf X}) ~|~ {\bf 0}, {\bf K}_{XX} \Bigr) \\ \\ p \bigl( {\bf y} \bigr) & = & N \left( {\bf y} ~|~ {\bf 0}, \frac{1}{\alpha}\Phi({\bf X}) {\Phi({\bf X})}^{\rm T} + \frac{1}{\beta} {\bf I} \right) \\ & = & N \Bigl( {\bf y} ~|~ {\bf 0}, {\bf K}_{XX} + \frac{1}{\beta} {\bf I} \Bigr) \\ \end{eqnarray} $$

2.4.2 ガウス過程による回帰モデルによる予測

　ここで、N+1 番目の未知のデータ に対する の予測値 を導出しましょう。

$$ y^{*} = f( {\bf x}^{*} ) + {\varepsilon}^{*} \\ f( {\bf x}^{*} ) = { \phi( {\bf x}^{*} ) }^{\rm T} {\bf w}, ~~~ {\varepsilon}^{*} \sim N \left( 0, \frac{1}{\beta} \right) $$

2.3.2 の結果から、 の予測分布は以下のように記述されます。

$$ f ( {\bf x}^{*} ) \sim N \Bigl( \mathbb{E} \left[ f ( {\bf x}^{*} ) \right] , \mathbb{V} \left[ f ( {\bf x}^{*} ) \right] \Bigr) $$ $$ \begin{eqnarray} \left\{ \begin{array}{c} \mathbb{E} \left[ f ( {\bf x}^{*} ) \right] & = & { {\bf k}^{*} }^{\rm T} { \left( {\bf K}_{XX} + \frac{1}{\beta} {\bf I} \right) }^{-1} {\bf y} \\ \mathbb{V} \left[ f ( {\bf x}^{*} ) \right] & = & k ( {\bf x}^{*}, {\bf x}^{*} ) - { {\bf k}^{*} }^{\rm T} { \left( {\bf K}_{XX} + \frac{1}{\beta} {\bf I} \right) }^{-1} {\bf k}^{*} \end{array} \right. \end{eqnarray} $$

未知のデータ をガウス過程 に加えると、

$$ \begin{eqnarray} {{\bf K}_{XX}}^{*} & = & \left( \begin{array}{cccc} k( {\bf x}_1, {\bf x}_1 ) & \dots & k( {\bf x}_1, {\bf x}_N ) & k( {\bf x}_1, {\bf x}^{*} ) \\ \vdots & \ddots & \vdots & \vdots \\ k( {\bf x}_N, {\bf x}_1 ) & \dots & k( {\bf x}_N, {\bf x}_N ) & k( {\bf x}_N, {\bf x}^{*} ) \\ k( {\bf x}^{*}, {\bf x}_1 ) & \dots & k( {\bf x}^{*}, {\bf x}_N ) & k( {\bf x}^{*}, {\bf x}^{*} ) \\ \end{array} \right) \\ \\ & = & \left( \begin{array}{cc} {\bf K}_{XX} & {\bf k}^{*} \\ { {\bf k}^{*} }^{\rm T} & k( {\bf x}^{*}, {\bf x}^{*} ) \end{array} \right) \end{eqnarray} $$

ただし、 は以下のように記述されるベクトルです。 $$ \begin{eqnarray} {\bf k}^{*} & := & \left( \begin{array}{c} k( {\bf x}_1, {\bf x}^{*} ) \\ \vdots \\ k( {\bf x}_N, {\bf x}^{*} ) \end{array} \right) \\ \\ & = & \left( \begin{array}{c} C o v \left[ f( {\bf x}_1 ), f( {\bf x}^{*} ) \right] \\ \vdots \\ C o v \left[ f( {\bf x}_N ), f( {\bf x}^{*} ) \right] \end{array} \right) \\ \\ & = & \left( \begin{array}{c} { \phi( {\bf x}_1 )}^{\rm T} \left( \frac{1}{\alpha} {\bf I} \right) \phi( {\bf x}^{*} ) \\ \vdots \\ { \phi( {\bf x}_N )}^{\rm T} \left( \frac{1}{\alpha} {\bf I} \right) \phi( {\bf x}^{*} ) \end{array} \right) \\ \\ & = & \left( \begin{array}{c} \frac{1}{\alpha} \phi_{1}( {\bf x}_1 ) \phi_{1}( {\bf x}^{*} ) + \cdots + \frac{1}{\alpha} \phi_{M}( {\bf x}_1 ) \phi_{M}( {\bf x}^{*} ) \\ \vdots \\ \frac{1}{\alpha} \phi_{1}( {\bf x}_N ) \phi_{1}( {\bf x}^{*} ) + \cdots + \frac{1}{\alpha} \phi_{M}( {\bf x}_N ) \phi_{M}( {\bf x}^{*} ) \end{array} \right) \\ \\ & = & { \phi( {\bf x}^{*} ) }^{\rm T} \frac{1}{\alpha} {\bf I} ~ \Phi( {\bf X} ) \end{eqnarray} $$

3. ガウス過程回帰をPythonで実装

　実際に、ある関数からデータサンプルを作成して、ガウス過程による回帰モデル によってこれを近似します。今回は、以下のような平均関数 と共分散関数 を用いたガウス過程 と、それに従う回帰モデル を考えます。ここで、共分散関数としてRBFカーネル（Radial basis function kernel, Gaussian kernel）を採用しています。

$$ f(x) \sim \mathcal{GP} \left( m(x), k(x, x') \right) $$

この回帰モデルを用いて、関数：

$$ y = \sin(2 \pi x) + \cos(1.7 \times 2 \pi x) ~~~ (0 \leq x \leq 1) $$

を、生成されるデータサンプルから予測してみましょう。なお実装は、こちらのQuitta記事を参考にさせてもらいました。

3.1 RBFカーネルのためのクラス

class RBFKernel(object):
    
    def __init__(self, sigma):
        self.sigma = sigma
        
    def get_sigma(self):
        return np.copy(self.sigma)

    def __call__(self, x1, x2):
        return np.exp( (-1. / (self.sigma ** 2) ) *  (x1 - x2) ** 2)

    def derivatives(self, x1, x2):
        dif_sigma = np.exp( (-1. / (self.sigma ** 2) ) *  (x1 - x2) ** 2) * ( (x1 - x2) ** 2 ) / ( self.sigma ** 3)
        return dif_sigma

    def update_sigma(self, update):
        self.sigma += update

3.2 ガウス過程回帰を行うためのクラス

class GaussianProcessRegression(object):

    def __init__(self, kernel, x, y, beta=1.):
        self.kernel = kernel
        self.x = x
        self.y = y
        self.beta = beta
        
        # グラム行列を計算
        self.fit_kernel()

    def fit_kernel(self):
        ''' グラム行列を計算 '''
        
        # グラム行列 K
        self.gram = self.kernel(*np.meshgrid(self.x, self.x))
        # 共分散行列 K + 1/beta I
        self.covariance = self.gram + np.identity(len(self.x)) / self.beta
        # 精度行列 (共分散行列の逆行列)
        self.precision = np.linalg.inv(self.covariance)
    
    def predict_y(self, x_new):
        ''' y_new の予測値と分散を出力 '''
        
        # k*
        k = np.array([self.kernel(xi, x_new) for xi in self.x])

        # 平均と分散
        y_mean = k.dot(self.precision.dot(self.y))
        y_var = self.kernel(x_new, x_new) - k.dot(self.precision.dot(k))
        
        return y_mean, y_var

3.3 グラフの描画（100フレームのアニメーション）を作成する

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation

def func(x):
    ''' 回帰モデルによって近似を行う関数 '''
    return np.sin(2 * np.pi * x) + np.cos(1.7 * 2 * np.pi * x)


def create_data_sample(func, low=0, high=1., n=10, std=1.):
    ''' n 組のデータサンプル (x, y) を作成する '''
    x = np.random.uniform(low, high, n)
    y = func(x) + np.random.normal(scale=std, size=n)
    return x, y
    
def _update(frame, x_data, y_data):
    ''' フレームごとにグラフを描画する '''
        
    # 現在のグラフを消去する
    plt.cla()
    
    # データサンプルのframe数分の取得
    x = x_data[:frame]
    y = y_data[:frame]
    
    # 回帰モデルをつくる
    kernel = RBFKernel(sigma=0.5)
    regression = GaussianProcessRegression(kernel, x, y, beta=100)
    
    # 描画用にxのデータを生成
    x_test = np.linspace(0, 1, 100)
    
    # yの予測値の平均と分散を導出
    y_test=[]
    y_var=[]
    for x_new in x_test:
        y_new_mean, y_new_var = regression.predict_y(x_new)
        y_test.append(y_new_mean)
        y_var.append(y_new_var)
        
    # list を numpy.ndarrayに変換
    y_test = np.array(y_test)
    y_var = np.array(y_var)
    
    # グラフを描画
    plt.scatter(x, y, alpha=0.4, color="blue", label="data sample")
    plt.plot(x_test, func(x_test), color="blue", linestyle="dotted", label="actual function")
    plt.plot(x_test, y_test, color="red", label="predicted function")
    plt.fill_between(x_test, y_test - 3 * np.sqrt(y_var), y_test + 3 * np.sqrt(y_var), color="pink", alpha=0.5, label="95% confidence interval (2 * std)")
    plt.legend(loc="lower left")
    plt.xlabel("x")
    plt.ylabel("y")
    plt.xlim([-0, 1])
    plt.ylim([-2.1, 2.1])
    plt.title("Gaussian Process Regression \n (RBF kernel, sigma=0.5, sample size = " + str(frame) + ")")
    
def main():
    # 描画領域
    fig = plt.figure(figsize=(8, 6))

    # データサンプルを作成
    x_data, y_data = create_toy_data(func, low=0, high=1, n=100, std=0.1)

    params = {
        'fig': fig,
        'func': _update,  # グラフを更新する関数
        'fargs': (x_data, y_data),  # 関数の引数 (フレーム番号を除く)
        'interval': 1,  # 更新間隔 (ミリ秒)
        'frames': np.arange(1, 101, 1),  # フレーム番号を生成するイテレータ, 1~100
        'repeat': False,  # 繰り返さない
    }

    # アニメーションを作成する
    ani = animation.FuncAnimation(**params)

    # アニメーションを保存する
    ani.save("./gpr_rbf.gif")
    # アニメーションを表示する
    # plt.show()

3.4 結果：アニメーションの描画

　 　サンプルサイズ（データ点の数）が増えると、徐々に回帰モデルで予測した関数（predicted function）が真の関数（actual function）に近づいていることがわかります。

4. 参考書籍

Gaussian Processes for Machine Learning (Adaptive Computation and Machine Learning series)

Pattern Recognition and Machine Learning (Information Science and Statistics)

ガウス過程の基礎 - 赤穂昭太郎, 2018

指数分布とワイブル分布をPythonでプロットしてみる

　生存時間解析など、応用範囲の広い指数分布についてまとめます。指数型分布族の仲間としては、ワイブル分布・ガンマ分布の他にも、ポアソン分布、レイリー分布、ラプラス分布（両側指数分布）などがあります。

1. 前提

1.1 確率分布の定義

　指数分布の確率密度関数 と累積分布関数 は、次のように定義されます。

• 指数分布

$$ X \sim Exp(\lambda), ~~~ \lambda \geq 0 $$

$$ \begin{eqnarray} f(x | \lambda) & = & \lambda ~ exp \left( - \lambda x \right) ~~~ (x \geq 0) \\ F(x | \lambda) & = & 1 - exp \left( - \lambda x \right) ~~~ (x \geq 0) \\ \end{eqnarray} $$ $$ \begin{eqnarray} \mathbb{E}\left[ X \right] & = & \frac{1}{\lambda} \\ \mathbb{V}\left[ X \right] & = & \frac{1}{\lambda^{2}} \end{eqnarray} $$

　また、ワイブル分布は、次のように定義されます。なお、 は、ガンマ関数*1（階乗を一般化したもの）です。

• ワイブル分布

$$ X \sim Weibull(\alpha, \beta), ~~~ \alpha \geq 0, ~~~ \beta \geq 0 $$

$$ \begin{eqnarray} f(x | \alpha, \beta) & = & \frac{\alpha}{\beta} { \left( \frac{x}{\beta} \right) }^{\alpha - 1} \left\{ - { \left( \frac{x}{\beta} \right) }^{\alpha} \right\} ~~~ (x \geq 0) \\ F(x | \alpha, \beta) & = & 1 - exp\left\{ - {\left( \frac{x}{\beta} \right) }^{a} \right\} ~~~ (x \geq 0) \\ \end{eqnarray} $$ $$ \begin{eqnarray} \mathbb{E}\left[ X \right] & = & \beta ~ \Gamma \left( 1 + \frac{1}{\alpha} \right) \\ \mathbb{V}\left[ X \right] & = & \beta^{\large \frac{2}{\alpha}} \left\{ \Gamma(1 + \frac{2}{\alpha}) - {\left( \Gamma(1 + \frac{1}{\alpha}) \right)}^{2} \right\} \end{eqnarray} $$

1. 2 指数分布とワイブル分布の関係

　ワイブル分布のパラメータをそれぞれ とすると指数分布に一致します。つまり、ワイブル分布は、指数分布の一般に拡張したものになります。

$$ Exp(\lambda) = Weibull(1, \frac{1}{\lambda}) $$

ちなみに、以下で定義されるガンマ分布のパラメータをそれぞれ とすると指数分布に一致します。

$$ Exp(\lambda) = Weibull(1, \frac{1}{\lambda}) = Gamma(1, \frac{1}{\lambda}) $$

• ガンマ分布

$$ X \sim Gamma(\alpha, \beta) $$

$$ \begin{eqnarray} f(x | \alpha, \beta) & = & \frac{1}{\Gamma(\alpha)} \frac{1}{\beta} {\left( \frac{x}{\beta} \right) }^{\alpha - 1}~~~ (x \gt 0) \\ \end{eqnarray} $$ $$ \begin{eqnarray} \mathbb{E}\left[ X \right] & = & \alpha \beta \\ \mathbb{V}\left[ X \right] & = & \alpha {\beta}^{2} \end{eqnarray} $$

2. Pythonによる実装

2.1 指数分布

python で分布を定義して、グラフをプロットしてみます。

import math
import random
import numpy as np
import matplotlib.pyplot as plt

# 指数分布

class Exp():
    def __init__(self):
        pass
    
    # 密度関数f
    def f(self, x, la=1):
        return la * math.exp(-1 * la * x)
    
    # 分布関数F
    def F(self, x, la=1):
        return 1 - math.exp(-1 * la * x)
    
    # Fの逆関数(samplingに使う)
    def invF(self, y, la=1):
        return -1 * (1 / la) * math.log(1 - y)
    
    # サンプリング
    def sampling(self, num, la):
        sample=[]
        for i in range(num):
            rand = random.random()
            sample.append(self.invF(rand, la))
        return np.array(sample)
    
    # 散布図
    def scatter_pdf(self, ax, data, la, alpha=0.4):
        pdf=[]
        for d in data:
            pdf.append(self.f(d, la))

        ax.scatter(data, pdf, alpha=alpha)
        ax.set_title("Exponential (lambda={:.2f})".format(la))
        ax.set_xlabel("value")
        ax.set_ylabel("probability density")
        ax.set_ylim(0, 1)
        
    # グラフ
    def plot_pdf(self, ax, data, la):
        pdf=[]
        for d in data:
            pdf.append(self.f(d, la))

        ax.plot(data, pdf)
        ax.set_title("Exponential (lambda={:.2f})".format(la))
        ax.set_xlabel("value")
        ax.set_ylabel("probability density")
        ax.set_ylim(0, 1)

実際にグラフを描画してみます。パラメータ の値を変えて、分布の形状をみます。

# グラフをmatplotlibで描画してみる

data = np.linspace(0, 15, 100)

fig, ax = plt.subplots(3, 3, figsize=(18, 18))

Exp().plot_pdf(ax[0, 0], data, 0.2)
Exp().plot_pdf(ax[0, 1], data, 0.4)
Exp().plot_pdf(ax[0, 2], data, 0.6)
Exp().plot_pdf(ax[1, 0], data, 0.8)
Exp().plot_pdf(ax[1, 1], data, 1)
Exp().plot_pdf(ax[1, 2], data, 1.2)
Exp().plot_pdf(ax[2, 0], data, 1.4)
Exp().plot_pdf(ax[2, 1], data, 1.6)
Exp().plot_pdf(ax[2, 2], data, 1.8)

plt.show()

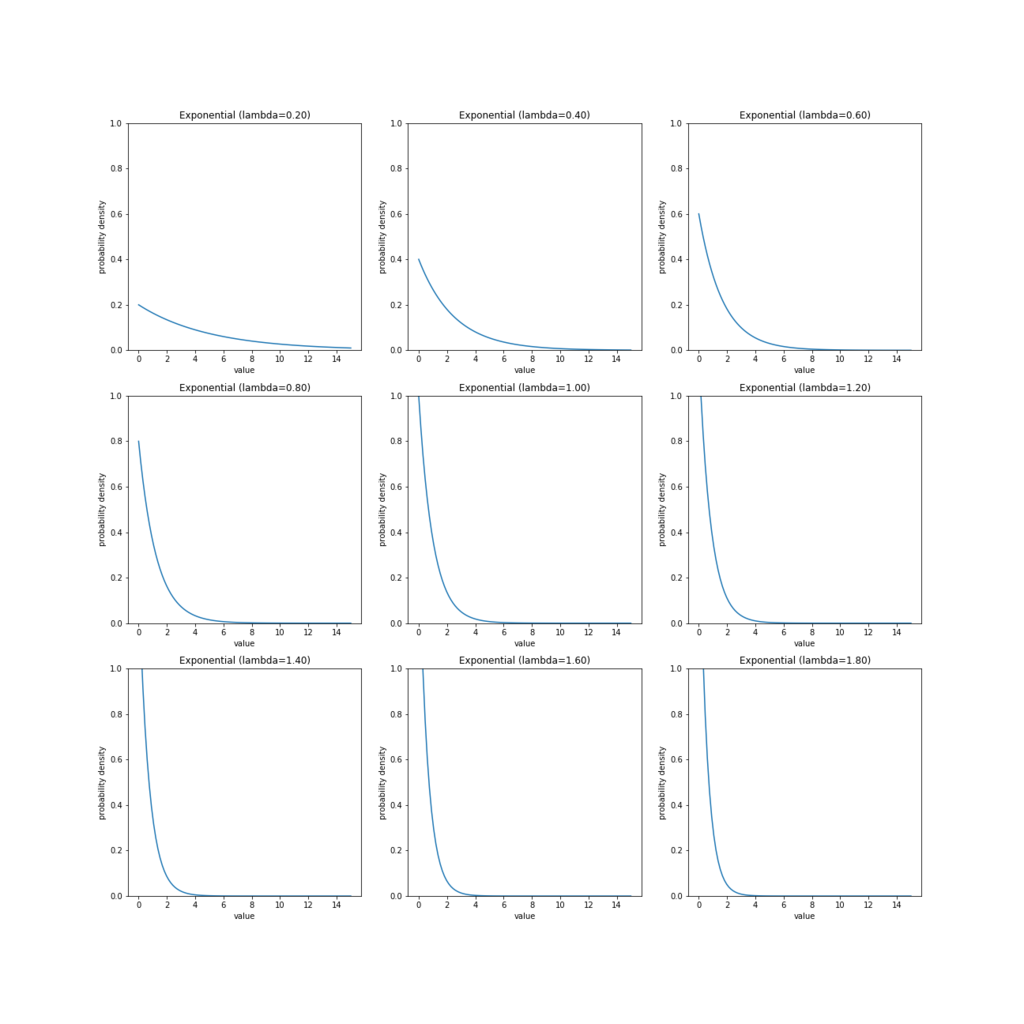
　プロットをみると、指数分布のパラメータ は、尺度（ばらつき）を表していることがわかります。分布は が大きくなるにつれ急峻になり、ばらつきが少なくなっていきます。平均について 、分散について となることから、「指数分布はパラメータ を上げると、平均は０に接近し、分散は限りなく小さくなる（０になる）」ということがわかります。

2.2 ワイブル分布

python で分布を定義して、グラフをプロットしてみます。

import math
import random
import numpy as np
import matplotlib.pyplot as plt

# ワイブル分布

class Weibull():
    def __init__(self):
        pass
        
    # 密度関数f
    def f(self, x, a, b):
        return (a/b) * ( (x/b)**(a - 1) ) * math.exp(-1 * (x/b)**a )
    
    # 分布関数F
    def F(self, x, a, b):
        return 1 - math.exp(-1 * (x/b)**a )
    
    # Fの逆関数
    def invF(self, y, a, b):
        return b * ( -1 * math.log(1 - y) )**(1/a)
    
    # サンプリング
    def sampling(self, num, a, b):
        sample=[]
        for i in range(num):
            rand = random.random()
            sample.append(self.invF(rand, a, b))
        return np.array(sample)
    
    # 散布図
    def scatter_pdf(self, ax, data, a, b, alpha=0.4):
        pdf=[]
        for d in data:
            pdf.append(self.f(d, a, b))

        ax.scatter(data, pdf, alpha=alpha)
        ax.set_title("Weibull (alpha={:.2f}, beta={:.2f})".format(a, b))
        ax.set_xlabel("value")
        ax.set_ylabel("probability density")
        ax.set_ylim(0, 1)
        
    # グラフ
    def plot_pdf(self, ax, data, a, b):
        pdf=[]
        for d in data:
            pdf.append(self.f(d, a, b))

        ax.plot(data, pdf)
        ax.set_title("Weibull (alpha={:.2f}, beta={:.2f})".format(a, b))
        ax.set_xlabel("value")
        ax.set_ylabel("probability density")
        ax.set_ylim(0, 1)

実際にグラフを描画してみます。パラメータ の値を変えて、分布の形状をみます。

# グラフをmatplotlibで描画してみる

data = np.linspace(0, 15, 100)

fig, ax = plt.subplots(3, 3, figsize=(18, 18))

Weibull().plot_pdf(ax[0, 0], data, 1, 1)
Weibull().plot_pdf(ax[0, 1], data, 1, 2)
Weibull().plot_pdf(ax[0, 2], data, 1, 3)
Weibull().plot_pdf(ax[1, 0], data, 2, 1)
Weibull().plot_pdf(ax[1, 1], data, 2, 2)
Weibull().plot_pdf(ax[1, 2], data, 2, 3)
Weibull().plot_pdf(ax[2, 0], data, 3, 1)
Weibull().plot_pdf(ax[2, 1], data, 3, 2)
Weibull().plot_pdf(ax[2, 2], data, 3, 3)

plt.show()

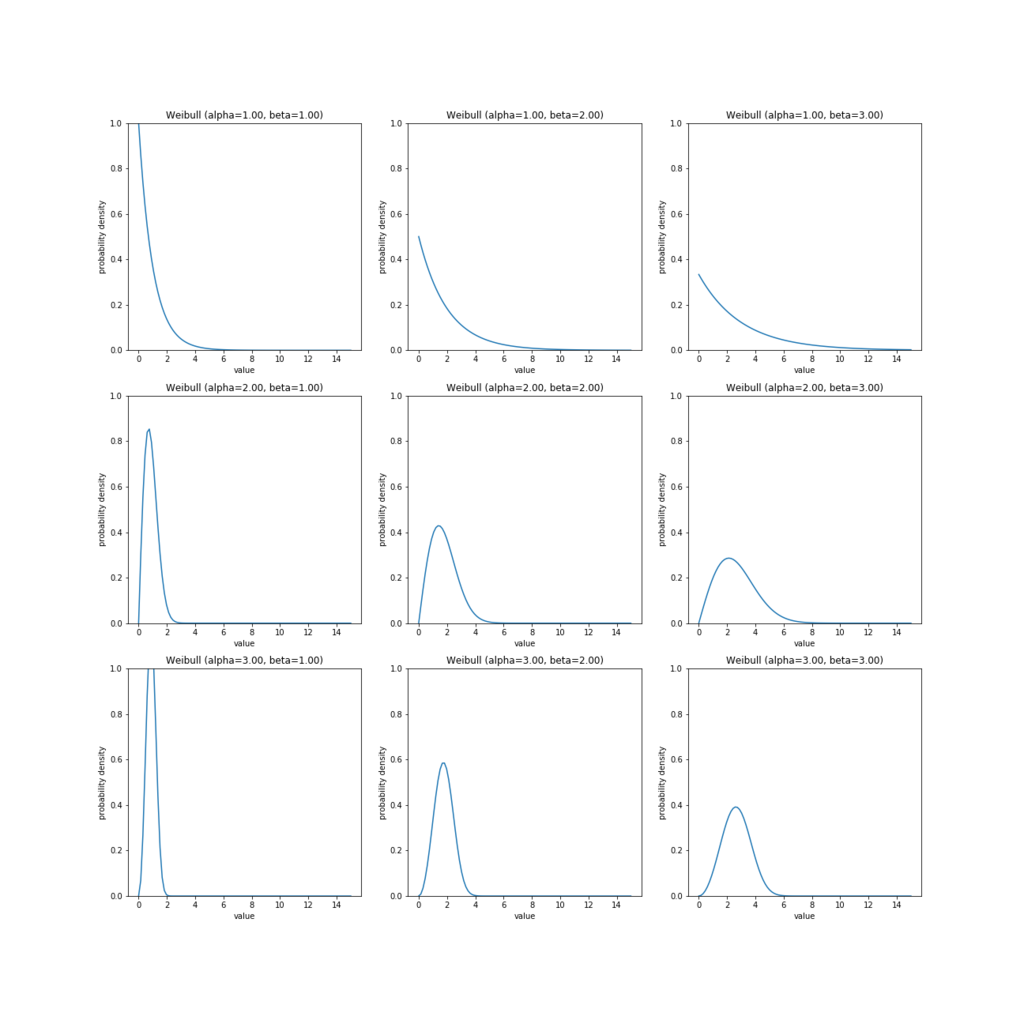
　プロットをみると、ワイブル分布のパラメータ は分布の形状を表し、パラメータ は、尺度（ばらつき）を表していることがわかります。実際、分布の形状は によって支配されており、ワイブル分布は のとき指数分布、 のときレイリー分布と一致します。分布は が大きくなるにつれ急峻になり、ばらつきが少なくなっていきます。

*1:ガンマ関数は、$$ \Gamma(n):=\int_{0}^{\infty} y^{n - 1} e^{-y} dy $$と定義され、 が自然数ならば が成り立つ。

Kullback-Leibler Divergenceについてまとめる

!! お知らせ（2020.06.10） * こちらの記事の英語版を公開しました．よければご覧ください．
Here is the english translation of this post. Please check it if you want.

1. KL-divergenceとは?

　統計学や情報理論をはじめとした広い分野で、KL-divergence*1はたびたび登場します。KL-divergenceは、「尤度比（尤もらしさを比較する尺度）を log 変換し（乗算操作を線形結合に直す、凸関数だから最適化との相性良い）、期待値（確率密度の重み付きの積分、ルベーグ積分）をとったもの」として定義されます。

1.1 定義

　一般に、確率分布 が確率密度関数 をもつとき、KL-divergence（Kullback-Leibler divergence）は、以下のように定義されます。

\begin{eqnarray} D_{KL}( Q \mid\mid P ) := \int q(x) \log \frac{q(x)}{p(x)} ~dx \tag{1} \end{eqnarray}

1.2 基本的な性質

　KL-divergenceは以下のような性質をもちます。

• （非負性）非負の値域をもつ。

\begin{align} 0 \leq D_{KL}( Q \mid\mid P ) \leq \infty \tag{2.1} \end{align}

• （完備性）値が 0 のとき、2つの確率分布 P と Q は同等。

\begin{align} D_{KL}( Q \mid\mid P ) = 0 ~~ \Leftrightarrow ~~ P = Q \tag{2.2} \end{align}

• （非対称性）値は P と Q に対して対称性を持たない。

\begin{align} D_{KL}( Q \mid\mid P ) \neq D_{KL}( P \mid\mid Q ) \tag{2.3} \end{align}

• （絶対連続性）値が発散しない限り、Q は P に関して絶対連続である。

\begin{align} D_{KL}( Q \mid\mid P ) \lt \infty ~~ \Rightarrow ~~ P \gg Q \tag{2.4} \end{align}

　例として、2つの正規分布間でKL-divergenceを計算*2すると、以下のような値になります。分布のズレが大きくなるほど、値が増加していることがわかります。

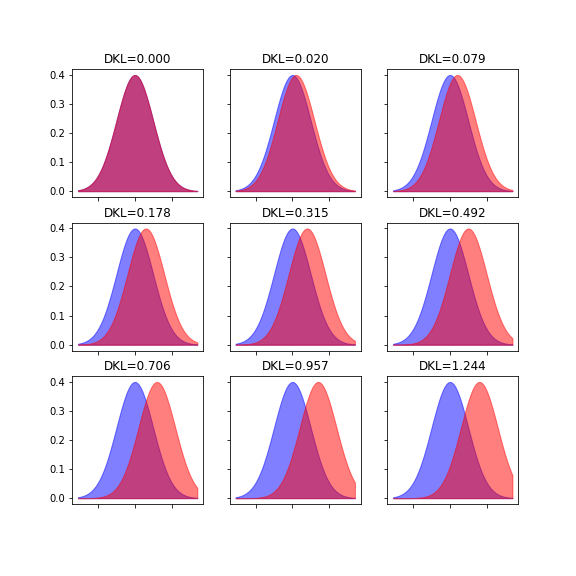
1.3 KL-divergenceは距離なのか？

　KL-divergenceは、確率や情報を考える際にとても重要な量であるため、分野や文脈によって様々な名称で呼ばれます。

"KL-divergence"
"KL-metrics"
"KL-information"
"Information divergence"
"Information gain"
"Relative entropy"

　KL-divergenceはつねに非負の値をとるため、これは確率分布 P と Q が存在する空間における距離(metrics)を示していると解釈することができます。しかし、KL-divergenceは次の距離の公理のうち「非負性」と「完備性」しか満たさないため、厳密には 距離(metrics) ではありません。

距離 の公理

1. 非負性　　　　
2. 完備性　　　　
3. 対称性　　　　
4. 三角不等式　　

　例えば、ユークリッド距離、二乗距離、マハラビノス距離、ハミング距離などは、この4つの条件をすべて満たすため、明らかに距離(metrics)として扱うことができます。一方で、KL-divergenceは距離(metrics)ではなくdivergenceです。"divergence"とは、距離の公理における４つの条件のうち「非負性」「対称性」のみを採用したものであり、"距離(metrics)"の拡張概念です。距離の公理による制約を減らし、抽象度の高い議論をしようというわけです。

　なお、このdivergenceという語は発散と訳されることが一般的で、例えば物理学ではベクトル作用素 div として登場します。divergenceのイメージに該当する日本語はありませんが、相違度、分離度、逸脱度、乖離度などが使われているようです。

　実例として、2つの正規分布 （青）と （赤）の間のKL-divergenceを測ってみましょう。左が青からみた赤とのKL距離、右が赤からみた青とのKL距離となっており値が異なることがわかります。なお「等分散正規分布間のKL-divergence」という特殊な条件下では、対称性が成り立ちます。

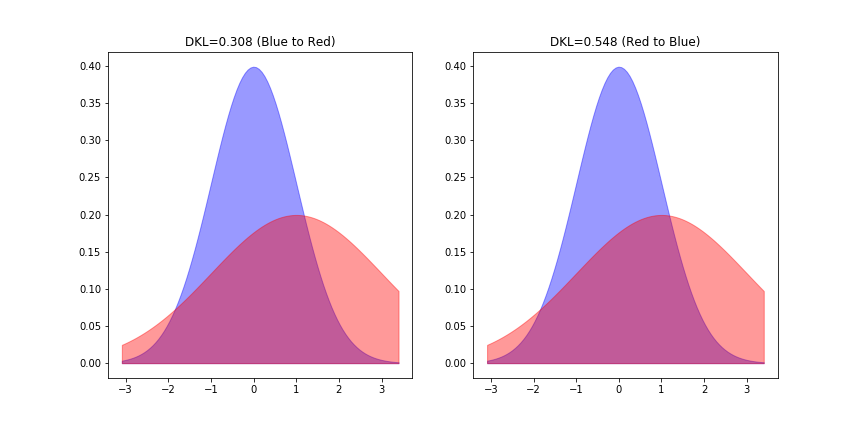
また，確率分布間の近さを測る尺度としては，KL情報量の他にも次のようなものが知られています．

確率分布 間の"距離"を測る量

• 　　　　　　　　 統計量

• 　　　　　　 -ノルム

• 　　　　　 -ノルム

• 　　 ヘリンジャー距離

• 　　　　　　 -ダイバージェンス 　

• 　 　 一般化情報量(Kawada, 1987)

• 　　 　　 KL情報量

2. 諸量との関係

2.1 KL-divergenceと相互情報量

　エントロピー 、結合エントロピー 、条件つきエントロピー 、相互情報量 は、確率密度 を用いて以下のように定義されます。*3

\begin{align} H(X) & := - \int Pr(x) \log Pr(x) ~dx \tag{3.1} \\ H(X,Y) & := - \int Pr(x,y) \log Pr(x,y) ~dy~dx \tag{3.2} \\ H(X|Y) & := - \int Pr(x,y) \log Pr(x|y) ~dx~dy \tag{3.3} \\ MI(X,Y) & := \int \int Pr(x,y) \log \frac{Pr(x,y)}{Pr(x)Pr(y)} ~dxdy \tag{3.4} \end{align}

2つの確率変数 X, Y について、相互情報量 MI（: Mutual Information）によって相互の関係性が明示されます。

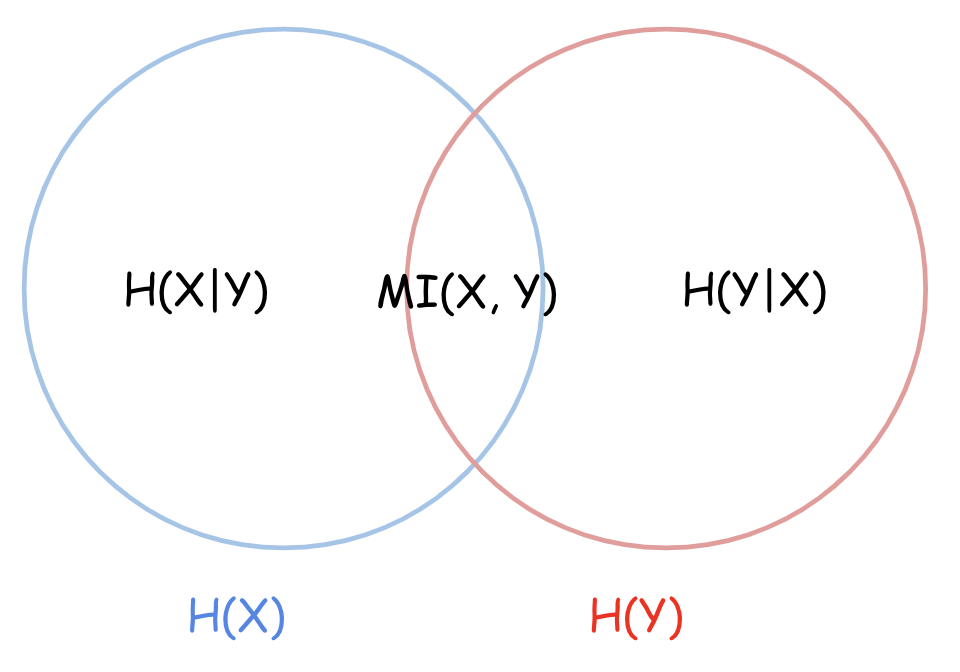
\begin{align} MI(X,Y) & = H(X) - H(X|Y) \tag{3.5.1} \\ & = H(Y) - H(Y|X) \tag{3.5.2} \\ & = H(X) + H(Y) - H(X,Y) \tag{3.5.3} \end{align}

　ここで、KL-divergenceと相互情報量 MI には以下の関係が成り立ちます。つまり、相互情報量 MI(X, Y) は、「確率変数 X と Y が独立でない場合の同時分布 P(X, Y)」と「独立である場合の同時分布 P(X)P(Y)」 の離れ具合（平均的な乖離度合い）を示しているのだと解釈できます。

\begin{align} MI(X, Y) & = D_{KL} \bigl( Pr(x, y) \mid\mid Pr(x)Pr(y) \bigr) \tag{3.6.1} \\ & = \mathbb{E}_{Y} \bigl[ D_{KL} \bigl( Pr(x|y) \mid\mid Pr(x) \bigr) \bigr] \tag{3.6.2} \\ & = \mathbb{E}_{X} \bigl[ D_{KL} \bigl( Pr(y|x) \mid\mid Pr(y) \bigr) \bigr] \tag{3.6.3} \\ \end{align}

（例）3.6.2の式展開

\begin{eqnarray} MI(X,Y) & = & \int \int Pr(x,y) \log \frac{Pr(x,y)}{Pr(x)Pr(y)} ~dxdy \\ & = & \int \int Pr(x|y)Pr(y) \log \frac{Pr(x|y)Pr(y)}{Pr(x)Pr(y)} ~dxdy \\ & = & \int Pr(y) \int Pr(x|y) \log \frac{Pr(x|y)}{Pr(x)} ~dx~dy \\ & = & \int Pr(y) \cdot D_{KL} \bigl( Pr(x|y) \mid\mid Pr(x) \bigr) ~dy \\ & = & \mathbb{E}_{Y} \bigl[ D_{KL} \bigl( Pr(x|y) \mid\mid Pr(x) \bigr) \bigr] \end{eqnarray}

2.2 KL-divergenceと対数尤度比

　ベイズ推定や統計モデリングでは、しばしば「真の分布 を、（パラメータの推定値 と確率モデル の組み合わせ）推定する」というモチベーションが起こります。そのため、２つの分布のズレを測りたいとき、あるいは推定誤差を損失関数やリスク関数に組み込んでパラメータに対する最適化問題をときたいときに、KL-divergenceを使います。

　KL-divergenceは最尤法をベースに、尤度比検定（Likelihood ratio test）、ベイズ因子（Bayse factor）、赤池情報量基準（AIC, Akaike's Information Critation）などのモデル選択手法*4と深い関わりを持ちます。

• 　真の分布 に対する推定分布 のKL-divergence： は次式のように、「 と の対数尤度比に対して、真の分布 で平均操作をおこなった値」です。

\begin{align} \left( 対数尤度比 \right) = \log \frac{q(x)}{p(x)} \tag{4} \end{align}

\begin{eqnarray} D_{KL}( Q \mid\mid P ) & := & \int q(x) \log \frac{q(x)}{p(x)} ~dx \\ & = & \mathbb{E}_{X} \left[ \log \frac{q(x)}{p(x)} \right] \left(: 平均対数尤度比 \right) \tag{5.1} \\ \end{eqnarray}

　　モデル比較・選択の評価値としてKL-divergenceを用いる場合、次式のように「KL-divergenceを最小にすること」と「平均対数尤度を最大にする」ことは等価になります。

\begin{eqnarray} D_{KL}( Q \mid\mid P ) & = & \mathbb{E}_{X} \bigl[ \log q(x) \bigr] - \mathbb{E}_{X} \bigl[ \log p(x) \bigr] \tag{5.2} \\ & \propto & - \mathbb{E}_{X} \bigl[ \log p(x) \bigr] \left(: - 平均対数尤度 \right) \tag{5.3} \end{eqnarray}

• パラメトリックな確率モデル （例えば線形回帰モデル）を考えた場合、何らかの損失関数 に対して最適なパラメータ と、その推定値 に対して、確率モデルの誤差は以下のようにKL-divergenceで表現されます。（ただし、 を対数尤度関数とする。）

\begin{align} \left( 対数尤度比 \right) = \log \frac{f(x|\theta_{0})}{f(x|\hat{\theta})} \tag{6} \end{align}

\begin{eqnarray} \hat{\theta} & :=& \underset{\theta \in \Theta}{\rm argmin} ~ L(\theta) \tag{7} \\ \\ D_{KL}( \theta_{0} \mid\mid \hat{\theta} ) & := & \int f(x|\theta_{0}) \log \frac{f(x|\theta_{0})}{f(x|\hat{\theta})} ~dx \\ & = & \mathbb{E}_{X} \left[ \log \frac{ f(x|\theta_{0}) }{ f(x|\hat{\theta}) } \right] \tag{8.1} \\ & = & \mathbb{E}_{X} \bigl[ \ell( \theta_{0}|x ) \bigr] - \mathbb{E}_{X} \bigl[ \ell( \hat{\theta}|x ) \bigr] \tag{8.2} \end{eqnarray}

2.3 KL-divergenceとFisher情報量

　確率モデル を仮定したとき、パラメータ のFisher情報量 は以下のように定義されます。（ただし、 を対数尤度関数とする。）

\begin{eqnarray} I(\theta) & := & \mathbb{E}_{X} \left[ { \left\{ \frac{d}{dx}\ell(\theta | x) \right\} }^{2} \right] \tag{9.1} \\ & = & \mathbb{E}_{X} \left[ { \left\{ \frac{d}{dx}\log f(x|\theta) \right\} }^{2} \right] \tag{9.2} \end{eqnarray}

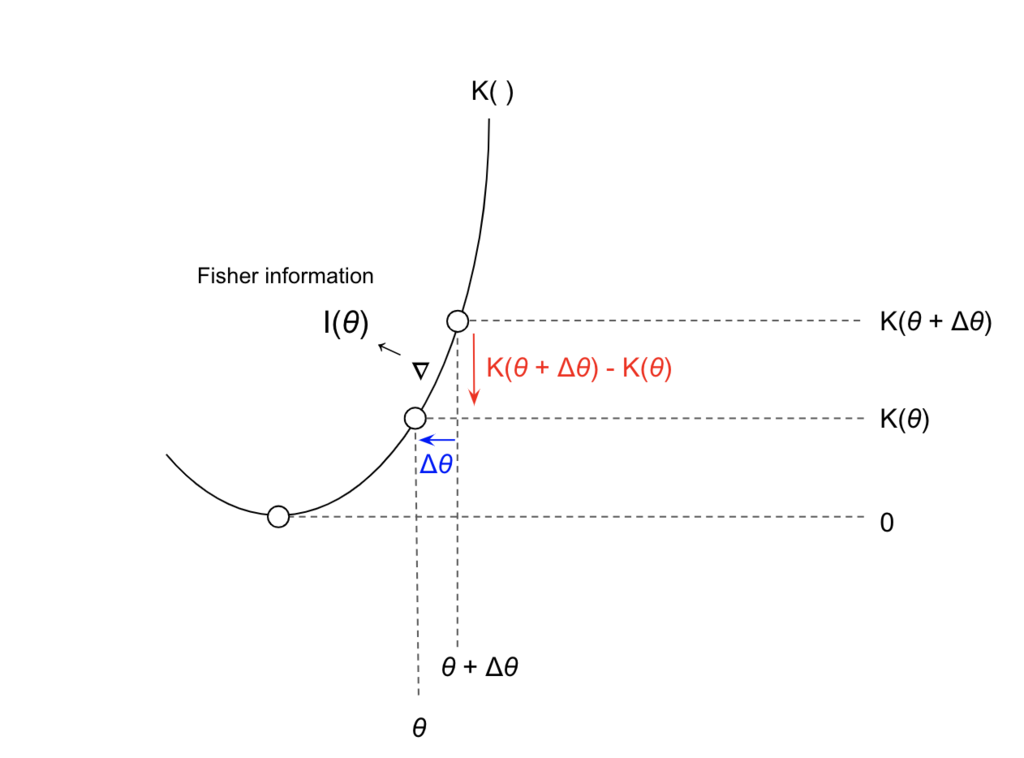
　 　確率モデル を仮定したとき、KL-divergenceとFisher情報量 の間には、次のような関係*5が成り立ちます。

\begin{eqnarray} \lim_{h \to 0} \frac{1}{h^{2}} D_{KL} \bigl( f(x|\theta) \mid\mid f(x|\theta+h) \bigr) = \frac{1}{2} I(\theta) \tag{10} \end{eqnarray}

　この式は、 の近傍でのKL-divergence： は、 における確率モデル のFisher情報量 に比例することを示しています。つまり、Fisher情報量 は確率モデル が の近傍でもつ局所的な情報量を表していることがわかります。

つまり，パラメトリックな確率モデルに対するKL-divergenceの微小変化はFisher情報行列を計量行列として計算できます．

\begin{eqnarray} D_{KL}(p_{\theta}, p_{\theta + \Delta \theta}) &= \int p(x|\theta) \log \frac{p(x|\theta)}{p(x|\theta+\Delta \theta)} dx \ &\approx \frac{1}{2} {\Delta \theta}^T I(\theta) \Delta \theta \end{eqnarray}

3. 参考書籍

新装改訂版 現代数理統計学

現代数理統計学の基礎 (共立講座 数学の魅力)

数理統計学 (数学シリーズ)

Elements of Information Theory (Wiley Series in Telecommunications and Signal Processing)

情報量規準 (シリーズ・予測と発見の科学)

*1:一般化するとf-divergenceというクラスが定義できます。汎関数微分などの関数解析の知識が必要。。

*2:pythonのライブラリ関数scipy.stats.entropyを使いました。

*3:熱力学的なエントロピーはボルツマン発祥ですが、シャノンの情報量に関する歴史的背景については以下で言及されています。ハートレー→ナイキスト→シャノンという流れがあるみたい。http://www.ieice.org/jpn/books/kaishikiji/200112/200112-9.html

*4:情報量規準についての文献→ https://www.ism.ac.jp/editsec/toukei/pdf/47-2-375.pdf

*5:この式は、KL-divergenceをテイラー展開して二次形式で近似すると導出されます。$$ \ell(\theta + h) - \ell(\theta) = {\ell}^{'}(\theta)h + \frac{1}{2} {\ell}^{''}(\theta) h^{2} + O(h^{3}) $$

最尤推定・MAP推定・ベイズ推定を比較する

1. 推定のモチベーション

　確率変数 の真の分布 に対して、

$$ \begin{cases} 確率モデル　 ：　p(X|w) \\ 事前分布　　 ：　\varphi(w) \end{cases} $$

を仮定したとき、

$$ データサンプル 　　：　X^{n} := \left\{ X_1, \dots ,X_n \right\} $$

を用いて、 を推定したい。

2. 最尤推定（ML）

2.1 パラメータ の対数尤度

ベイズの定理： $$ \begin{eqnarray} p(w | X^{n}) = \frac{ p(X^{n}|w) \varphi(w) }{ \int_{W} p(X^{n}|w) \varphi(w) dw} \end{eqnarray} $$

において、以下で定義される対数尤度 は、手元にあるサンプルデータ に対する 、確率モデル の尤もらしさを示します。対数尤度 の示す値は、サンプルデータ がもつ"ばらつき"が加味されておらず、手元にあるデータの値に大きく依存するということに注意してください。

$$ \begin{eqnarray} \ell(w | \cdot) & := & \log p(\cdot | w) \\ \\ \ell(w | X^{n}) & := & \log p(X^{n} | w) \\ & = & \log \prod_{i=1}^{n} p(X_i | w) \end{eqnarray} $$

2.2 パラメータの推定（最尤推定量）

　最尤推定では、対数尤度 が最大となるようなパラメータ を選び、これを確率モデル におけるパラメータ の推定量とします。推定量 を最尤推定量と呼びます。

$$ \begin{eqnarray} \hat{w}_{ML} := \underset{w \in W}{\rm argmax} ~ \ell(w|X^{n}) \end{eqnarray} $$

以上から、最尤推定では、確率変数 の真の分布 は、サンプルデータ から求めた最尤推定量 と確率モデル によって次式のように推定されます。

$$ \begin{eqnarray} q(X) \approx p( X | \hat{w}_{ML} ) \end{eqnarray} $$

3. 事後確率最大化推定（MAP）

3.1 パラメータ の事後確率

ベイズの定理：

$$ \begin{eqnarray} p(w | X^{n}) = \frac{ p(X^{n}|w) \varphi(w) }{ \int_{W} p(X^{n}|w) \varphi(w) dw} \end{eqnarray} $$

において、以下で定義される事後確率 は、手元にあるサンプルデータ に対する 、確率モデル ・事前分布 の尤もらしさを示します。事後確率 の示す値は、サンプルデータ がもつ"ばらつき"が加味されておらず、その値に大きく依存するということに注意してください。

$$ \begin{eqnarray} p(w | \cdot) & := & \frac{1}{Z} \log p(\cdot | w)\varphi(w) \\ \\ p(w | X^{n}) & := & \frac{1}{Z_n} \log p(X^{n} | w)\varphi(w) \\ & = & \frac{1}{Z_n} \log \prod_{i=1}^{n} p(X_i | w)\varphi(w) \end{eqnarray} $$

• ただし、 は、それぞれベイズの定理における右辺の分子に対して で積分した値（正規化定数）を表す。

3.2 パラメータの推定（MAP推定量）

　MAP推定では、事後確率が最大となるようなパラメータ を選び、これを確率モデル におけるパラメータ の推定量とします。推定量 をMAP推定量と呼びます。

$$ \begin{eqnarray} \hat{w}_{MAP} := \underset{w \in W}{\rm argmax} ~ p(w|X^{n}) \end{eqnarray} $$

　以上から、MAP推定では、確率変数 の真の分布 は、サンプルデータ から求めたMAP推定量 と確率モデル によって次式のように推定されます。
$$ \begin{eqnarray} q(X) \approx p( X | \hat{w}_{MAP} ) \end{eqnarray} $$

4. ベイズ推定（Bayse）

4.1 パラメータ の平均対数尤度

ベイズの定理： $$ \begin{eqnarray} p(w | X^{n}) = \frac{ p(X^{n}|w) \varphi(w) }{ \int_{W} p(X^{n}|w) \varphi(w) dw} \end{eqnarray} $$

において、以下で定義される平均対数尤度 は、 に対して期待値をとった（ のばらつきによる偶然誤差を排除した）上での、確率モデル の尤もらしさを示します。

$$ \begin{eqnarray} K(w) & := & \mathbb{E}_{X} \left[ \log p(X | w) \right] \tag{期待対数尤度} \\ \\ K_n(w) & := & \frac{1}{n} \sum_{i=1}^{n} \log p(X_i | w) \tag{経験対数尤度} \end{eqnarray} $$

パラメータの推定量を求めるため、平均対数尤度を符号反転したものを、損失関数 として定義します。

$$ \begin{eqnarray} L(w) & := & - K(w) = \mathbb{E}_{X} \left[ - \log p(X | w) \right] \tag{期待損失関数} \\ \\ L_n(w) & := & - K_{n}(w) = \frac{1}{n} \sum_{i=1}^{n} \left\{ - \log p(X_i | w) \tag{経験損失関数} \right\} \end{eqnarray} $$

4.2 確率分布 の推定（予測分布）

　ベイズ推定では、損失関数が最小となるようなパラメータ を選び、これを確率モデル と事前分布 によって求められる事後分布 の平均値の推定量とみなします。ここで、最尤推定やMAP推定では、「確率モデル に対して与えるパラメータ はある1つの値に決まる」と仮定していますが、ベイズ推定では「パラメータ は事前分布 によって確率的に変動する値（=確率変数）である」と仮定していることに注意します。推定量 をベイズ推定量*1と呼びます。

$$ \begin{eqnarray} \hat{w}_{0} := \underset{w \in W}{\rm argmax} ~ L_{n}(w) \end{eqnarray} $$

　推定量 は「事後分布において がとり得ると期待される（尤もらしい）値」と考えられます。しかし、ベイズ推定において、確率変数 の真の分布 を、 によって推定することはしません。その代わり、推定量 を平均にもつ事後分布 から求められる予測分布 を用いて真の分布 を推定します。

$$ \begin{eqnarray} q(X) \approx p^{*}(X) & := & \int_{W} p(X|w)p(w|X^{n}) dw \end{eqnarray} $$

　上図は、確率モデル・事前分布・事後分布がすべて正規分布に従う場合の各分布を表す。Prior（事前分布）の「ばらつき」に対して、Likelihood（尤度, 最尤推定で用いる）と Posterior（事後分布, MAP推定で用いる）は、より小さい「ばらつき」をもつ。

5. 参考図書

StanとRでベイズ統計モデリング (Wonderful R)

データ解析のための統計モデリング入門――一般化線形モデル・階層ベイズモデル・MCMC (確率と情報の科学)

ベイズ統計の理論と方法

*1:他の言い方もあるようです。

確率変数に関する4つの「収束概念」

　確率変数の収束（Convergence of random variables） についてまとめてみました。数理統計学において極限現象の解析は特に重要で、漸近理論、極値理論、大偏差理論などで収束概念は欠かせません。
　解析学において、数列の極限から関数の極限を定義したように、統計学（確率論）においても確率変数列の極限から確率変数の極限を定義します。

1. 確率収束 : convergence in probability

確率変数列 に対して、任意の(どんなに小さな) について、 $$ \begin{eqnarray} \lim_{n \to \infty} P(~|U_n-U|{\geq}{\varepsilon}~) = 0 \end{eqnarray} $$ が成り立つとき、「確率変数列 は、確率変数 に確率収束する」といい、これを $$ \begin{eqnarray} U_n \underset{~~~~~p}{\to} U \end{eqnarray} $$ と表記する。

2. p次平均収束 : convergence in mean

確率変数列 に対して、 $$ \begin{eqnarray} \lim_{n \to \infty} E \left[~{|U_n-U|}^{~p} \right] = 0 \end{eqnarray} $$ が成り立つとき，「確率変数列 は、確率変数 にp次平均収束する」という。 　
　

3. 分布収束（法則収束）: convergence in distribution (law)

確率変数列 に対して、確率変数 の分布関数 の任意の連続点 で、 $$ \begin{eqnarray} \lim_{n \to \infty} P( U_n \leq x ) & = & P( U \leq x) \\ & = & F_U(x) \end{eqnarray} $$ が成り立つとき、「確率変数列 は、確率変数 に分布収束（法則収束）する」といい、これを、 $$ \begin{eqnarray} U_n \underset{~~~~~d}{\to} U \end{eqnarray} $$ と表記する。 　
　

4. 概収束 : almost sure convergence

確率変数列 に対して、 $$ \begin{eqnarray} P\left( \omega~{\large |}~{\lim_{n \to \infty} \left| U_n(\omega)-U( \omega ) \right| =0} \right) = 1 \end{eqnarray} $$

が成り立つとき，「確率変数列 は、確率変数 に概収束する」といい，これを、 $$ \begin{eqnarray} U_n \to U ~~~ a.s. \end{eqnarray} $$ と表記する。 　 　 　 　 　

参考文献

現代数理統計学の基礎 (共立講座 数学の魅力)

現代数理統計学 (創文社現代経済学選書)

入門確率過程

ベイズ推定の流れをまとめる（尤もらしさと不確実性）

ベイズ推定とは？

ベイズ推定の目的と主眼をまとめると、次のようになります。

• ベイズ推定の目的
  確率変数 の真の分布 を、予測分布 で推定する。
  また、推定プロセスで生じる誤差や、推定結果に対する信頼性を評価したい。

このポストでは、『ベイズ統計の理論と方法』（渡辺澄夫, 2012）の内容を基に、ベイズ推定の基本の流れを整理するとともに、ベイズ推定で行われる「尤度最大化」と「情報量最小化」は同じであることを軸に、各統計量についての解説・解釈を述べたいと思います。

ベイズ統計の理論と方法

これから言及する「ベイズ推定の流れ」を、簡単にまとめました。

「ベイズ推定の流れ」

• 真の分布 　　　:　

に対して、

• 確率モデル　　：　
• 事前分布　　　：　

を仮定したとき、

• データ（標本）

を用いて、以下の分布・統計量を求める。

• 事後分布　　　：　
• 予測分布　　　：　
• 期待損失関数　：　
• 経験損失関数　：　
• 期待誤差関数　：　
• 経験誤差関数　：　
• 汎化損失　　　：　
• 経験損失　　　：　

1. 事後分布

　まず、確率モデル と事前分布 から、パラメータ の事後分布 を導出します。ベイズの定理より、

$$ \begin{eqnarray} p(w|X_n) & = & \frac{ p(X_{n}|w)\varphi(w) }{ p(X_{n}) } \\ \\ p(w|X_n) & = & \frac{ p(X_{n}|w)\varphi(w) }{ \int_{w} p(X_{n}|w)\varphi(w) dw } \end{eqnarray} $$

となります。さらに、右辺の分母を正規化定数 とおけば、事後分布は以下のように定義することができます。

$$ \begin{eqnarray} p(w|X_n):=\frac{1}{Z} p(X_n|w)\varphi(w) \end{eqnarray} $$ ただし、 $$ \begin{eqnarray} Z:=\int_{w} p(X_{n}|w)\varphi(w) dw \end{eqnarray} $$

2. 予測分布

　事前分布 を事後分布 におきかえて、再び確率モデル のパラメータ に対する期待値をとります。

$$ \begin{eqnarray} p^{*}(x)=p(x|X_n):=\int_{w} p(x|w)p(w|X_n) dw \end{eqnarray} $$

ここまでの流れをまとめると、次のようになります。

1. 確率モデル と事前分布 を設定する。
2. 確率モデル と事前分布 によって、事後分布 を導出する。
3. 確率モデル と事後分布 によって、予測分布 を導出する。
4. 予測分布 によって、真の分布 を推定する。

次に、確率モデルの推定誤差を定量化する統計量（標本に対する関数）や、推定誤差を小さくするパラメータ の推定量 を求めてみましょう。

3. 損失関数

　「パラメータ の対数尤度の に対する期待値」として、損失関数 を定義します。損失関数 は、確率モデル とパラメータ によって、決定されます。 を期待損失関数、 を経験損失関数と呼びます。実際には、真の分布 がわからず期待損失関数 を求められないので、データ を用いて、経験損失関数 を導出することになります。

$$ \begin{eqnarray} L(w) & := & E_{X} \left[ -\log p(X|w) \right] \\ \\ L_n(w) & := & \frac{1}{n} \sum_{i=1}^{n} -\log p(X_i|w) \end{eqnarray} $$

よって、データ から導出される経験損失関数 に対して、パラメータ の最適化問題を考えることができます。確率モデル における、パラメータ の推定量 を以下で定めます。

$$ \begin{eqnarray} w_0:=\underset{w \in W}{\rm argmin} ~ L_n(w) \end{eqnarray} $$

• 推定量 について：
  　 は、確率モデル によって推定された「データ に対する情報量（曖昧さ、不確実性）」を示しています。すなわち、ベイズ推定における推定量 は、「データ に対する不確実性を、平均的に最小化するようなパラメータ 」であると意味づけられます。

• 損失関数 について：
  　 は、「あるパラメータ を与えたとき、確率モデル がデータ に対してもつ平均的な不確実性」を表していると解釈できます。

4. 誤差関数

「任意のパラメータ に対する推定量 との誤差」として誤差関数 を定義します。まず、パラメータ と その推定量 との誤差を、次の対数尤度比で定義します。

$$ \begin{eqnarray} f(x,w):= \log \frac{ p(x|w_0) }{ p(x|w) } \end{eqnarray} $$

　対数尤度比 を用いて、誤差関数 を定義します。 を期待誤差関数、 を経験誤差関数と呼びます。ここで、実際には真の分布 がわからず期待誤差関数 を求められないから、データ を用いて、経験誤差関数 を導出することになります。

$$ \begin{eqnarray} K(w) & := & E_{X} \left[ f(X,w) \right]=E_{X} \left[ \log \frac{ p(X|w_0) }{ p(X|w) } \right] \\ \\ K_{n}(w) & := & \frac{1}{n} \sum_{i=1}^{n} f(X_i, w)=\frac{1}{n} \sum_{i=1}^{n} \log \frac{p(X_i|w_0)}{p(X_i|w)} \end{eqnarray} $$

• 対数尤度比 について：
  対数尤度比を分解すると、 $$ \begin{eqnarray} f(x, w) := \log \frac{ p(x|w_0) }{ p(x|w) } = \left[ -\log p(x|w) \right] - \left[ -\log p(x|w_0) \right] \geq 0 \end{eqnarray} $$ と表されるため、これは、あるパラメータ を与えたときの確率モデル がもつ「尤もらしさ」を、「尤もらしさの上限」で正規化した値を示します。別の見方をすると、対数尤度比： は、確率モデル がもつ「データ に対する不確実性」を、「最小の不確実性」で正規化した値とも考えられます。
• 誤差関数 について：
  は、「あるパラメータ を与えたとき、確率モデル がデータ に対してもつ平均的な（正規化された）尤もらしさ」を表していると解釈できます。

5. 汎化損失・経験損失

　「予測分布 と真の分布 との誤差」として、「推定方法」がもつ損失を定義します。 を汎化損失、 を経験損失と呼びます。

$$ \begin{eqnarray} G_{n} & := & E_{X} \left[ -\log p^{*}(X) \right] \\ \\ T_{n} & := & \frac{1}{n} \sum_{i=1}^{n} - \log p^{*}(X_i)　 \end{eqnarray} $$

• 汎化損失 について：
  は、予測分布 によって推定された「データ に対する情報量（曖昧さ、不確実性）」を示します。すなわち、汎化損失 は、「パラメータ とデータ を与えたとき、確率モデル から推定された予測分布 が、データ に対してもつ平均的な不確実性」を表していると解釈できます。

• 汎化損失 と KL-距離 の比例関係
  $$ \begin{eqnarray} G_n &=& E_{X} [ -\log p^{*}(X) ] \\ \\ &=& \int_{X} q(x) \cdot -\log p^{*}(X) dx \\ \\ &=& - \int_{X} q(x) \log q(x) dx + \int_{X} q(x) \log \frac{q(x)}{p^{*}(x)} dx \\ \\ &=& H(X)+D_{KL}(q \parallel p^{*}) \end{eqnarray} $$ ここで、確率モデル と上式の関係を考えると、は、確率モデル に依らないから無視できます。つまり、汎化損失 は の真の分布 と予測分布 の間のカルバック・ライブラー距離（Kullback–Leibler divergence）は、確率モデル に対して比例関係にあります。

$$ \begin{align} G_n \propto D_{KL}(q \parallel p^{*}) \end{align} $$

• KL-距離 について：
  真の分布 と予測分布 の間のカルバック・ライブラー距離（Kullback–Leibler divergence）の定義式は、 $$ \begin{eqnarray} D_{KL}(q \parallel p^{*}) := \int_{X} q(x) \log \frac{q(x)}{p^{*}(x)} dx \end{eqnarray} $$ ですから、これは「対数尤度比 の確率変数 に対する期待値」として解釈できます。例として、下図右は、2つの正規分布 と について、それぞれの分布に従う確率変数 の各値を横軸に、それによって計算される対数尤度比を縦軸にとったグラフを示しています。よって、 は、その期待値ですから、下図右で青く塗りつぶされた部分の「確率重みつき面積（期待値）」となります。