閃 き

閃き- blog

きらびやかに、美しく、痛烈に．

Johnson and Lindenstrauss Lemmaとその構成論的証明

数学 統計学

f:id:yumaloop:20190620010600p:plain:w500

ランダム行列理論（Random projection）の基本定理であるJohnson and Lindenstrauss Lemmaについて解説します． JL-補題は「変換前後でサンプル点どうしのユークリッド距離を変えない」ような関数 f の存在を主張しており，これは具体的にランダム行列 A を用いた線形写像として構成できます．

JL-補題

d次元空間 Q \subset {\mathbb{R}}^{d}上にある n 個のサンプル点を考える．任意の \epsilon \in (0,1) について，

$$ k \geq \frac{4 \log n}{ {\epsilon}^{2}/2 - {\epsilon}^{3}/{3}} $$

をみたす整数 k に対して，以下をみたす f: \mathbb{R}^{d} \to \mathbb{R}^{k} が存在する．

$$ \newcommand{\norm}[1]{\left\lVert#1\right\rVert} \forall u,v \in Q \subset {\mathbb{R}}^{d}, \\ (1 - \epsilon)\norm{u - v}^{2} \leq \norm{ f(u) - f(v) }^{2} \leq (1 + \epsilon) \norm{ u - v }^{2} $$

構成論的証明

写像 f: \mathbb{R}^{d} \to \mathbb{R}^{k} として， k \times d のランダム行列 A で定義される線形写像 f_Aを考える．

$$ {f}_{A}(x) = \frac{1}{\sqrt{k}} Ax \\ where~A_{ij} ~ {\scriptsize i.i.d.} \sim \mathcal{N}(0,1) $$

まず，正規分布の線形性・再生性*1より，

$$ \newcommand{\norm}[1]{\left\lVert#1\right\rVert} \begin{eqnarray} A_{ij}(x_{j}) &\sim& \mathcal{N}\left( 0, {x_{j}}^{2} \right) \\ {\{Ax\}}_{j} &\sim& \mathcal{N}\left( 0, \norm{ x }^{2} \right) \end{eqnarray} $$

が成り立つ．正規化して変数 Z_jを定義すれば，これは標準正規分布に従う．

$$ Z_j = \frac{{\{Ax\}}_{j}}{\norm{x}} \sim \mathcal{N}\left( 0, 1 \right) $$

さらに，

$$ \norm{Ax}^{2} = \sum_{j=1}^{k} {\{Ax\}}_{j}^{2} $$

が成り立つことに注意すると，

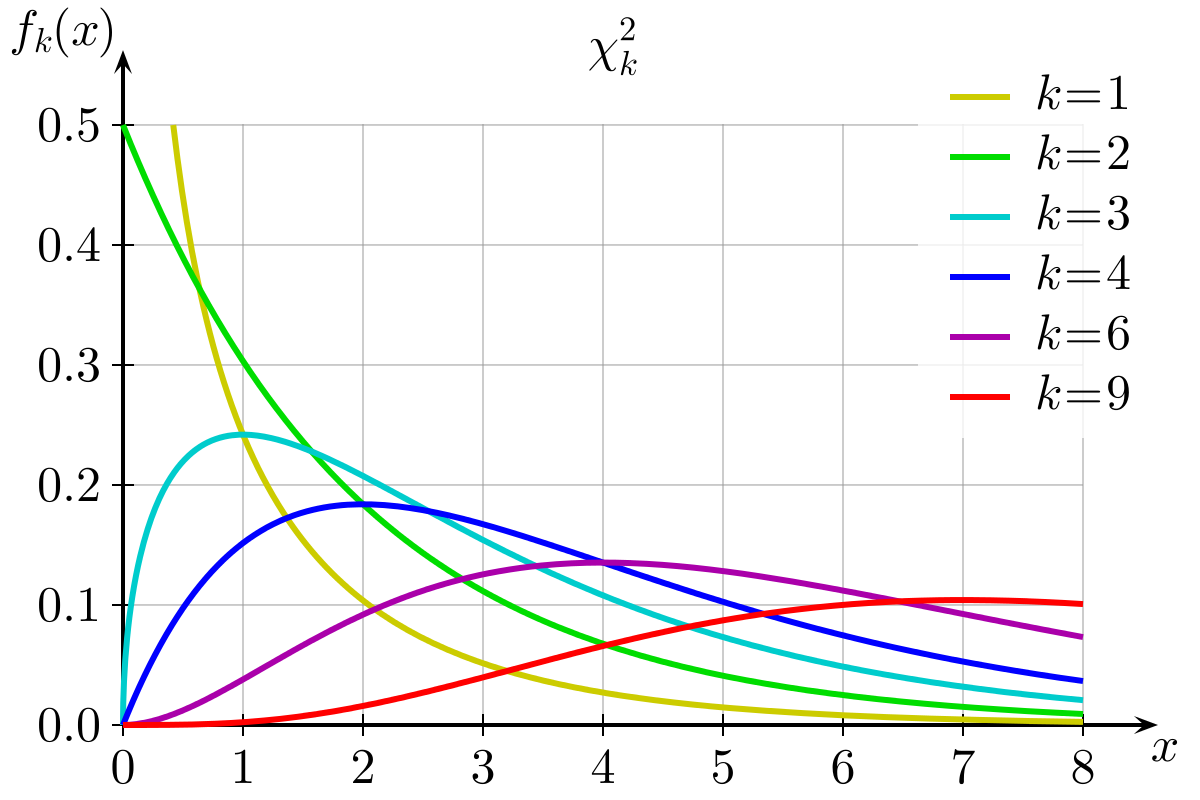
$$ \frac{\norm{Ax}^{2}}{\norm{x}^{2}} = \sum_{j=1}^{k} \frac{{\{Ax\}}_{j}^{2}}{\norm{x}^{2}} = \sum_{j=1}^{k} {Z_j}^{2} \sim \chi_{k}^{2} $$

となる．すなわち，行列 A による線形変換の前後で，ノルムを考えるとき，これはカイ二乗分布によって評価できる．

$$ \begin{eqnarray} Pr\left( \norm{f_{A}(x)}^{2} \lt (1 + \varepsilon) \norm{x}^{2} \right) &=&Pr\left( \norm{ \frac{1}{\sqrt{k}} Ax }^{2} \lt (1 + \varepsilon) \norm{x}^{2} \right) \\ &=& Pr\left( \norm{ Ax }^{2} \gt (1 + \varepsilon) k \norm{x}^{2} \right) \\ &=& Pr\left( \frac{\norm{ Ax }^{2}}{\norm{x}^{2}} \gt (1 + \varepsilon) k \right) \\ &=& Pr\left( \sum_{j=1}^{k} {Z_j}^{2} \gt (1 + \varepsilon)k \right) \\ &=& Pr\left( \chi_{k}^{2} \geq (1 + \varepsilon)k \right) \end{eqnarray} $$

次に自由度 k のカイ二乗分布 \chi_{k}^{2} を表す確率密度関数を考え，上式の右辺を上から抑えたい．

$$ p(\cdot | k) = \frac{1}{{2}^{\frac{k}{2}} \Gamma \left( \frac{k}{2} \right) } {x}^{\frac{k}{2} - 1} {e}^{- \frac{x}{2}} $$

https://upload.wikimedia.org/wikipedia/commons/thumb/3/35/Chi-square_pdf.svg/1200px-Chi-square_pdf.svg.png

ややテクニカルだが，確率密度分布から不等式を整理していく．途中で定数 \lambda \in (0, \frac{1}{2}) を導入している．

$$ \begin{eqnarray} Pr \left( \chi_{k}^{2} \geq (1 + \varepsilon)k \right) & = & Pr \left( \sum_{i=1}^{k} Z_{i}^{2} \gt (1 + \varepsilon)k \right) \\ & = & Pr \left( e^{\sum_{i=1}^{k} Z_{i}^{2}} \gt e^{(1 + \varepsilon)k} \right) \\ & = & Pr \left( e^{\lambda \sum_{i=1}^{k} Z_{i}^{2}} \gt e^{ \lambda (1 + \varepsilon)k} \right) ~~~ (0 \lt \lambda \lt \frac{1}{2}) \\ & \leq & \frac{\mathbb{E}[e^{\lambda \sum_{i=1}^{k} Z_{i}^{2}}] }{e^{(1 + \varepsilon)k \lambda}} \\ & = & \frac{{ \left( \mathbb{E}[ e^{\lambda {Z_{1}^{2}}} ] \right) }^{k}}{e^{(1 + \varepsilon)k \lambda}} \\ & = & e^{-(1 + \varepsilon) k \lambda } {\left( \frac{1}{1 - 2 \lambda} \right)}^{\frac{k}{2}} \end{eqnarray} $$

ここで， \lambda = \frac{\varepsilon}{2(1 + \varepsilon)} を代入すれば，

$$ \begin{eqnarray} Pr \left( \chi_{k}^{2} \geq (1 + \varepsilon)k \right) & = & {\left( (1 + \varepsilon)e^{- \varepsilon} \right) }^{\frac{k}{2}} \\ & \leq & \exp \left( - \frac{k}{4} ( {\varepsilon}^{2} - {\varepsilon}^{3} ) \right) \end{eqnarray} $$

が求められる．ただし．

$$ 1 + \varepsilon \leq \exp \left( \varepsilon - \frac{{\varepsilon}^{2} - {\varepsilon}^{3}}{2} \right) $$

を使った．以上をまとめると，ランダム行列 A を用いて構成される写像

$$ {f}_{A}(x) = \frac{1}{\sqrt{k}} Ax \\ where~A_{ij} ~ {\scriptsize i.i.d.} \sim \mathcal{N}(0,1) $$

に対して，

$$ \begin{eqnarray} Pr\left( \norm{f_{A}(x)}^{2} \geq (1 + \varepsilon) \norm{x}^{2} \right) & \leq & \exp \left( - \frac{k}{4} ( {\varepsilon}^{2} - {\varepsilon}^{3} ) \right) \\ Pr\left( \norm{f_{A}(x)}^{2} \leq (1 + \varepsilon) \norm{x}^{2} \right) & \geq & \exp \left( - \frac{k}{4} ( {\varepsilon}^{2} - {\varepsilon}^{3} ) \right) \end{eqnarray} $$

が成り立つ．よって，JL-補題をみたす写像 f が構成された．


参考文献

*1:http://www.sguc.ac.jp/i/st/learning/statistics/hosoku/%E6%AD%A3%E8%A6%8F%E5%88%86%E5%B8%83%E3%81%AE%E5%86%8D%E7%94%9F%E6%80%A7.pdf

機械学習でよく使う評価指標まとめ

機械学習 統計学 Kaggle 備忘

f:id:yumaloop:20190528210419p:plain:w600


　このポストでは，機械学習でよく使われる評価指標を，回帰・分類に分けて整理します．また，各評価指標の定義だけではなく，その性質や使用上の注意点などにも言及しました．なお，"網羅性"を過度に追求して，世にある評価指標を片っ端からリストアップすると，ポストとしての目的が分からず，何より煩雑で見づらくなってしまうと思ったので，紹介する評価指標については，重要で汎用度の高いものに絞りました．

なお，このポストの内容は，CourseraにあるKaggle講座「How to Win a Data Science Competition: Learn from Top Kagglers」をまとめたものです． ja.coursera.org

　※ 評価指標については随時，追加・更新していく予定です．このポストの内容には多分に不足/不備が含まれていると思われますが，些細な点でも，コメントなどにてご指摘いただけるととても嬉しいです．

1. 回帰

  • Notation
    • N - number of data samples
    • y \in \mathbb{R}^{N} - target vector (data set)
    • \hat{y} \in \mathbb{R}^{N} - predicted vector (data set)
    • y_i \in \mathbb{R} - target value (data)
    • \hat{y}_{i} \in \mathbb{R} - predicted value (data)

1.1. MSE, RMSE, R2

  • MSE (Mean Square Error, 平均二乗誤差)

$$ MSE(\hat{y}) := \frac{1}{N}\sum_{i=1}^{N} { ( y_i - \hat{y}_{i} ) }^{2} $$

  • RMSE (Root Mean Square Error, 二乗平均平方根誤差)

$$ RMSE(\hat{y}) := \sqrt{ \frac{1}{N}\sum_{i=1}^{N} { ( y_i - \hat{y}_{i} ) }^{2} } $$

  • R2 (R-squared, 決定係数)

$$ {R^{2}}( \hat{y} ) := 1 - \frac{ \frac{1}{N} \sum_{i=1}^{N} { ( {y}_i - \hat{y}_{i} ) }^{2} }{ \frac{1}{N} \sum_{i=1}^{N} { ( {y}_i - \bar{y}) }^{2} } = 1 - \frac{M S E(\hat{y})}{Var(y)} $$

  • MSEについて
    • MSEは，回帰における最も基本的な評価指標
    • 予測値 \hat{y}の各要素を定数 \alphaで固定した場合（ \hat{y}_i = \alpha），最適な定数 \alpha^{*}_{MSE} は観測データ y の平均値 \bar{y}になる． $$ \alpha^{*}_{MSE} := \bar{y} = \frac{1}{N}\sum_{i=1}^{N} y_i $$
  • MSE, RMSE, R2の相違点
    • 損失関数としての性質
      • モデルの予測値 \hat{y}に対するモデルパラメータ \thetaの最適化を考える．MSE・RMSE・R2はいずれも同じ． $$ \begin{eqnarray} MSE(\hat{y}_{\theta_1}) & > & MSE(\hat{y}_{\theta_2}) \\ \Leftrightarrow RMSE(\hat{y}_{\theta_1}) & > & RMSE(\hat{y}_{\theta_2}) \\ \Leftrightarrow \hspace{1.37em} {R^{2}}(\hat{y}_{\theta_1}) & > & {R^{2}}(\hat{y}_{\theta_2}) \end{eqnarray} $$
      • パラメータの更新に，勾配法を使う場合は注意．
        • RMSEを損失関数にした場合，MSEよりも更新幅が小さくなる． $$ \frac{\partial RMSE}{\partial \hat{y}_{i}} = \frac{1}{2 \sqrt{MSE}} \frac{\partial MSE}{\partial \hat{y}_{i}} $$
    • モデルの絶対評価を行う際は，MSEではなくR2(決定係数)がよく使われる．


1.2. MAE

  • MAE (Mean Absolute Error, 平均絶対誤差)

$$ MAE(\hat{y}) := \frac{1}{N}\sum_{i=1}^{N} \left| y_i - \hat{y}_{i} \right| $$

  • MAEについて

    • 予測値 \hat{y}の各要素を定数 \alpha で固定した場合（ \hat{y}_i = \alpha），最適な定数 \alpha^{*}_{MAE}は観測データ yの中央値median(y)になる． $$ \alpha^{*}_{MAE} := median(y) $$
    • 損失関数としての性質
      • MAEを損失関数とする場合，勾配法はあまり使われない
      • 予測値 \hat{y}の各要素を定数 \alphaで固定した場合（ \hat{y}_i = \alpha），
        • \frac{\partial MAE}{\partial \hat{y}_{i}} ~ : ステップ関数 (原点では微分不可能)
        • \frac{{\partial}^{2} MAE}{\partial {\hat{y}_{i}}^{2}} : 常に0 (原点では微分不可能)
    • MSEよりも，データに対するロバスト性が高い．
      • データに外れ値があった場合，MSEが評価する誤差は，MAEの2倍．
      • データの平均値は外れ値に影響されるが，中央値は外れ値に対して頑健．
    • MSEよりも，指標としての解釈性が高い．

  • Huber損失

    • ：MSEとMAEをミックスさせた評価指標として，Huber損失*2がある．ロバスト推定やSVMの損失関数に用いられる． $$ Huber~loss := \frac{1}{N} \sum_{i=1}^{N} {L}_{\delta}(y_i, \hat{y}_{i}) \\ {L}_{\delta}(y_i, \hat{y}_{i}) = \left\{ \begin{array}{c} \frac{1}{2} {( y_{i} - \hat{y}_{i} )}^{2} \hspace{4em} ( |y_{i} - \hat{y}_{i}| \leq \delta ) \\
      \delta \cdot ( |y_{i} - \hat{y}_{i}| - \frac{1}{2}\delta) \hspace{1em} ( |y_{i} - \hat{y}_{i}| \gt \delta )
      \end{array} \right. $$
  • Quantile Regression (分位点回帰)


1.3. (R)MSPEとMAPE

  • MSPE (Mean Square Percentage Error, 平均平方二乗誤差率)

$$ MSPE(\hat{y}) := \frac{100}{N} \sum_{i=1}^{N} { \left( \frac{y_i - \hat{y}_{i} }{y_i} \right) }^{2} $$

  • MSAE (Mean Absolute Percentage Error, 平均絶対誤差率)

$$ MSAE(\hat{y}) := \frac{100}{N} \sum_{i=1}^{N} \left| \frac{y_i - \hat{y}_{i} }{y_i} \right| ~~~~~~~~ $$

  • 相対誤差と絶対誤差*4
    • 絶対誤差 = y_i - \hat{y}_{i}
    • 相対誤差 = (y_i - \hat{y}_{i}) ~/~ y_{i}
  • MSPEについて
    • MSEを相対誤差で評価したもの．
    • %表示（百分率）にすることが多い．
    • 例：観測値 y_iと予測値 \hat{y}_{i}（ N=1）が以下のような場合
      • If ({y}_{1} = 90, ~~~ \hat{y}_{1} = 100)~~ then, MSE=100,~~~~~MSPE=1
      • If ({y}_{2} = 900, ~ \hat{y}_{2} = 1000) then, MSE=10000,~MSPE=1
    • 損失関数としての性質
      • 予測値 \hat{y}の各要素を定数 \alphaで固定した場合（ \hat{y}_{i} = \alpha），最適な定数 \alpha^{*}_{MSPE} は観測データ y の重み付き平均値 w(\bar{y}) になる．
      • 値が小さいデータに対して過剰にfitしようとする．（バイアス）
  • MAPEについて
    • MAEを相対誤差で評価したもの．
    • %表示（百分率）にすることが多い．
    • 例：観測値 y_iと予測値 \hat{y}_{i}（ N=1）が以下のような場合
      • If ( y_1 = 90, ~~~ \hat{y}_1 = 100)~~ then, MAE=10,~~~MAPE=1
      • If ( y_2 = 900, ~ \hat{y}_2 = 1000) then, MAE=100,~MAPE=1
    • 損失関数としての性質
      • 予測値 \hat{y}の各要素を定数 \alphaで固定した場合（ \hat{y}_{i} = \alpha），最適な定数 \alpha^{*}_{MAPE} は観測データ yの重み付き中央値 w(med(y))になる．
      • 値が小さいデータに対して過剰にfitしようとする．（バイアス）


1.4. RMSLE

  • RMSLE (Root Mean Square Logarithmic Error, 平均平方二乗対数誤差)

$$ \begin{eqnarray} RMSLE(\hat{y}) &:=& \sqrt{ \frac{1}{N}\sum_{i=1}^{N} { \left\{ \log(y_i + 1) - \log(\hat{y}_{i} + 1) \right\} }^{2} } \\ &=& \sqrt{ MSE(\log(y_i + 1), \log(\hat{y}_{i} + 1) ) } \end{eqnarray} $$

  • RMSLEについて
    • MSEをlogスケールで表現したもの
    • 絶対誤差を，相対誤差(MSPE, MAPE)ではなくlogスケールで表現．
      y_i の大小を考慮して誤差評価
    • 損失関数として用いる場合， \hat{y} に対して凸かつ非対称
      • \hat{y} > 極小値 → 傾きが小さい
      • \hat{y} < 極小値 → 傾きが大きい



2. 分類

  • Notation
    • N - number of data samples
    • L - number of classes
    • y_i - ground truth (data)
    • \hat{y}_{i} - predictions (data)
    • y_{il} - probability that i-th sample belongs l-th label
    • \hat{y}_{il} - confidence that i-th sample belongs l-th label
    • [ a = b] - indicator factor
  • 混同行列 (Confusion matrix)*5
    • 二値分類(Binary classification)タスクのみに使う．
      • True Positive (TP)
        • Positiveサンプルのうち，正しくPositiveと分類されたもの
      • False Positive (FP)
        • Negativeサンプルのうち，間違ってPositiveと分類されたもの
      • False Negative (FN)
        • Positiveサンプルのうち，間違ってNegativeと分類されたもの
      • True Negative (TN)
        • Negativeサンプルのうち，正しくNegativeと分類されたもの

          f:id:yumaloop:20190601010758p:plain:w500

    • 代表的な評価指標*6
      • 正答率 (Accuracy) = (TP+TN) / (TP+FP+TN+FN)
      • 精度 (Precision) = TP / (TP+FP)
      • 検出率 (Recall) = TP / (TP+FN)
      • F値 (F-Measures) = \frac{2}{\frac{1}{Recall}+\frac{1}{Precision}}
    • ROC曲線 (Receiver Operating Curve, 受信者操作曲線)
      • しきい値 bを変化させたときの真陽性率 (TP Rate)と偽陽性率 (FP Rate)の関係を曲線でプロットしたもの
        • 真陽性率 (TP Rate) = TP / (TP+FN) = 感度 (Sensitivity) = 検出率 (Recall)
        • 偽陽性率 (FP Rate) = FP / (FP+TN)
        • 偽陰性率 (FN Rate) = FN / (TP+FN)
        • 真陰性率 (TN Rate) = TN / (FP+TN) = 特異度 (Specificity)

参考：Pang-Ning Tan, Introduction to Data Mining (2ndEdition), Chapter 3 "Classification: Basic Concepts and Techniques"


2.1. Accuracy

  • Accuracy (正答率)

$$ Accuracy := \frac{1}{N}\sum_{i=1}^{N} [ y_i = \hat{y}_{i} ] $$

  • Error (誤り率)

$$ Error := \frac{1}{N}\sum_{i=1}^{N} [ y_i \neq \hat{y}_{i} ] $$

  • Soft prediction と Hard prediction
    • soft labels (soft predictions)
      • f(x) \in \mathbb{R}^{L} - 分類モデル fの出力スコア
    • hard labels (hard predictions)
      • \underset{i}{\rm argmax} ~ f_{i} (x) - 分類モデル fが最大スコアを出力したラベル
      • \left[ b \lt f(x) \in \mathbb{R}^{L} \right]，b - しきい値
  • Accuracyについて
    • Hard predictionなので，解釈が難しい．
      • 分類モデル fの出力値そのものではなくて， argmaxで評価する．
    • 損失関数として用いると，最適化が難しい．
    • best conts. \alpha^{*}(x)：最も頻度の高いクラスに固定する．
    • 例（ N = 100）
      • Dataset
        • 10 cats
        • 90 dogs
      • \alpha^{*}(x) = "dogs"


2.2. LogLoss

  • Binary LogLoss

$$ Losloss := - \frac{1}{N}\sum_{i=1}^{N} \left\{ y_i \log \hat{y}_{i} + (1 - y_i) \log (1 - \hat{y}_i) \right\}, ~~ y_i, \hat{y}_{i} \in \mathbb{R} $$

  • Multiclass LogLoss

$$ Logloss := - \frac{1}{N} \sum_{i=1}^{N} \sum_{l=1}^{L} y_{il} \log \hat{y}_{il}, ~~ y_i, \hat{y}_{i} \in \mathbb{R}^{L} $$

  • LogLoss (Logarithmic loss)について
    • Soft prediction．
    • 損失関数として用いると，最適化が簡単．
    • best conts. \alpha^{*}_{i}(x)：i-th クラスの頻度（経験分布）
    • 例（ N = 100）
      • Dataset
        • 10 cats
        • 90 dogs
      • \alpha^{*}(x) = [0.1, 0.9 ]

2.3. AUC (ROC)

  • AUC (Area Under Roc)

AUC := Area under the ROC Curve

  • AUC (ROC) について
    • AUC*7は，二値分類(Binary classification)タスクのみに使う
    • サンプルに対する識別結果の"順序"にのみ依存，分類モデルの"出力値"には非依存．
    • best consts. \alpha^{*}_{i}(x)：任意の定数に固定してもAUCの値は同じ．
    • AUCの説明
      • ROC(Receiver Operating Curve)曲線の下側面積
        • Wilcoxon-Mann-Whitney検定 (WMW検定)
        • Brunner-Munzel検定
      • サンプルペアの順序
        • 正しい順序に分類されたサンプルペアの割合
        • AUC := \frac{correctly~orderd~pairs}{total~number~of~pairs}
    • pythonの場合，sklearn.metrics.roc_curve()とsklearn.metrics.auc()を使って計算できる．

2.4. Cohen’s Kappa

  • Cohen’s Kappa ( \kappa係数, \kappa統計量)

$$ Kappa := 1 - \frac{1 - accuracy}{1 - p_{e}} = 1 - \frac{error}{baseline~error} $$ $$ p_{e} := \frac{1}{N^{2}} \sum_{k} n_{k1} n_{k2} $$

　　　　　・ i - 評価者

　　　　　・ k - 識別するクラス

　　　　　・ n_{ki} - 評価者 iがクラス kであると識別したサンプルの数

　　　　　・ N - サンプルの数

　　　　　・ p_{e} - 各サンプルをランダムに識別した場合の平均正答率


  • Weighted Kappa (重み付けカッパ係数)

$$ Weighted~Kappa := 1 - \frac{weighted~error}{weighted~baseline~error} $$ $$ weighted~error := \frac{1}{Z} \sum_{i,j} c_{ij} w_{ij} $$

　　　　　・ c_{ij} - 混同行列 Cの (i, j)成分

　　　　　・ w_{ij} - 重み行列 Wの (i, j)成分

　　　　　・ Z - 規格化定数

  • Cohen's Kappa について
    • Jacob Cohenが1960年に発表．
    • 基準となるスコア(baseline)を0に正規化して，任意のモデルの性能を表現．
      • 「Kappa - Accuracy の関係性」は，「R2 - MSE の関係性」に似ている．
  • Weighted Kappaについて
    • Accuracy(Error)に重みづけを行ってKappaを計算．
      • weighted~error := \frac{1}{Z} \sum_{i,j} c_{ij} w_{ij}
      • c_{ij}：混同行列 C \in \mathbb{R}^{L \times L}の (i, j)成分　※ L - 識別するクラス数
      • w_{ij}：重み行列 W \in \mathbb{R}^{L \times L}の (i, j)成分　※ L - 識別するクラス数
    • 混同行列 C
      • TP, FP, FN, FP
    • 重み行列 W
      • "順序つき"クラスラベルの分類に使う．
      • 例：病気のレベルに応じたクラス分類
    • 重み行列 Wの構成法
      • Linear weights： w_{ij} = |i - j|
      • Quadratic weights： w_{ij} = {(i - j)}^{2}
    • Quadratic Weighted Kappaを損失関数に使う場合，典型的には，MSEで近似する*8．
    • 例（ N = 100）
      • Dataset
        • 10 cats
        • 90 dogs
        • 20 tigers

Kaggleで勝つデータ分析の技術

Kaggleで勝つデータ分析の技術

Python実践データ分析100本ノック

Python実践データ分析100本ノック

統計学入門 (基礎統計学Ⅰ)

統計学入門 (基礎統計学Ⅰ)

  • 発売日: 1991/07/09
  • メディア: 単行本

Pythonではじめる機械学習 ―scikit-learnで学ぶ特徴量エンジニアリングと機械学習の基礎

Pythonではじめる機械学習 ―scikit-learnで学ぶ特徴量エンジニアリングと機械学習の基礎

［第2版］Python機械学習プログラミング 達人データサイエンティストによる理論と実践 impress top gearシリーズ

［第2版］Python機械学習プログラミング 達人データサイエンティストによる理論と実践 impress top gearシリーズ

サーモス 真空断熱タンブラー 2個セット 400ml ステンレス JDI-400P S

サーモス 真空断熱タンブラー 2個セット 400ml ステンレス JDI-400P S

  • 発売日: 2017/03/01
  • メディア: ホーム&キッチン

*1:線形回帰モデルにのみ適用可能

*2:Huber, Peter J. (1964). “Robust Estimation of a Location Parameter”. Annals of Statistics 53 (1): 73–101. doi:10.1214/aoms/1177703732. JSTOR 2238020.

*3:"QUANTILE REGRESSION", Roger Koenker, http://www.econ.uiuc.edu/~roger/research/rq/rq.pdf

*4:参考：相対誤差の計算方法と意義

*5:参考：Understanding Confusion Matrix - Towards Data Science

*6:参考：Accuracy, Precision, Recall or F1? - Towards Data Science

*7:奥村先生によるAUC (ROC)の解説ページ：https://oku.edu.mie-u.ac.jp/~okumura/stat/ROC.html

*8:解析的に解く方法もある．"On The Direct Maximization of Quadratic Weighted Kappa"

Markdownエディタ "Typora" の紹介とショートカット [macOS Mojave 10.14.4]

備忘 計算機環境

Typoraの紹介

Typoraは，高機能＆シンプルなMarkdownエディタです．最大の特徴は，Markdownコードを書くと，エディタ上で即座にレンダリングされ，インタラクティブにプレビューが表示されることです．Markdownで表や数式をよく書く場合，この機能は思った以上に有用で，簡単なメモをサクッと書くときに便利です．また，PDFへのエクスポート機能も優秀で，Pandocで煩雑な設定をする必要なくドキュメントを印刷できます．

f:id:yumaloop:20190528120527p:plain:w600



ダウンロード

Typoraのインストーラ(.dmg)は，以下のURLからダウンロードできます．Macにダウンロードする場合は，画面下にある「Download Beta (OS X)」ボタンをクリックすればOKです．

https://typora.io/

f:id:yumaloop:20190528121014p:plain:w600


Typoraの詳しい紹介/解説としては，

qiita.com

qiita.com

などがありますが，Mac OS向けのショートカットがなかったので，このポストに載せておきます．


ショートカット (Mac OS)

macOSで動作するショートカットです．※ Typora OS X版 (β 0.9.9.24.6)

  • カーソル操作
    ショートカット 処理
    Command + / 編集モードを切替
    Command + D 単語を選択
    Command + F 単語を検索
    Command + shift + D 単語を削除
    Command + L 行を選択
    Command + enter 行を追加
    Command + E スコープ/セルを選択
    Command + J 次章にジャンプ
    Command + {↑, ↓} ファイルの最上行/最下行にジャンプ
    Command + {=, -} 見出しレベル（<p>から<h1>まで）を上下
    Command + ^ + {↑, ↓, ←, →} 表のセル内を移動
  • フォーマットの挿入
    ショートカット 処理
    Command + {1~5} 見出しh1~h5を挿入
    Command + {=, -} 見出しレベルをする
    Command + I 斜体**を挿入
    Command + B 太字****を挿入
    Command + U 下線<u></u>を挿入
    Command + K ハイパーリンク[](url)を挿入
    Command + option + L リンク[]: urlを挿入
    Command + option + Q 引用符>を挿入
    Command + option + B 数式ブロックを挿入
    Command + option + C コードブロックを挿入
    Command + option + T 表を挿入
    Command + control + I 画像![]を挿入
    [toc] 目次を挿入
    $$ 数式を挿入
  • ファイル操作
    ショートカット 処理
    Command + N 新しいファイルを開く
    Command + T 新しいタブを開く
    Command + shift + N 新しいウィンドウを開く
    Command + O 既存のファイルを選択して開く
    Command + W 現在のウィンドウを閉じる
    Command + S 現在のファイルを保存する
    Command + shit + L ファイル内のアウトラインを表示
    Command + shift + O ファイル名で検索


ショートカットの表をMarkdownファイルにコピペしたい方のために，生のmarkdownスクリプトを載せておきます！どうぞ． 

# Short cut (MacOS)

- カーソル操作

  | ショートカット             | 処理                                      |
  | -------------------------- | ----------------------------------------- |
  | Command + /                | 編集モードを切替                          |
  | Command + D                | 単語を選択                                |
  | Command + F                | 単語を検索                                |
  | Command + shift + D        | 単語を削除                                |
  | Command + L                | 行を選択                                  |
  | Command + enter            | 行を追加                                  |
  | Command + E                | スコープ/セルを選択                       |
  | Command + J                | 次章にジャンプ                            |
  | Command + {↑, ↓}           | ファイルの最上行/最下行にジャンプ         |
  | Command + {=, -}           | 見出しレベル（`<p>`から`<h1>`まで）を上下 |
  | Command + ^ + {↑, ↓, ←, →} | 表のセル内を移動                          |

- フォーマットの挿入

  | ショートカット        | 処理                          |
  | --------------------- | ----------------------------- |
  | Command + {1~5}       | 見出し`h1~h5`を挿入           |
  | Command + {=, -}      | 見出しレベルをする            |
  | Command + I           | 斜体`**`を挿入                |
  | Command + B           | 太字`****`を挿入              |
  | Command + U           | 下線`<u></u>`を挿入           |
  | Command + K           | ハイパーリンク`[](url)`を挿入 |
  | Command + option + L  | リンク`[]: url`を挿入         |
  | Command + option + Q  | 引用符`>`を挿入               |
  | Command + option + B  | 数式ブロックを挿入            |
  | Command + option + C  | コードブロックを挿入          |
  | Command + option + T  | 表を挿入                      |
  | Command + control + I | 画像`![]`を挿入               |
  | [toc]                 | 目次を挿入                    |
  | $$                    | 数式を挿入                    |

- ファイル操作

  | ショートカット      | 処理                           |
  | ------------------- | ------------------------------ |
  | Command + N         | 新しいファイルを開く           |
  | Command + T         | 新しいタブを開く               |
  | Command + shift + N | 新しいウィンドウを開く         |
  | Command + O         | 既存のファイルを選択して開く   |
  | Command + W         | 現在のウィンドウを閉じる       |
  | Command + S         | 現在のファイルを保存する       |
  | Command + shit + L  | ファイル内のアウトラインを表示 |
  | Command + shift + O | ファイル名で検索               |

Donsker-Varadhan representation（DV下限）

数学 統計学

定理（DV表現）

連続確率変数 X に対して，確率密度関数 q(x), p(x) が定義されているとき，以下の関係式が成り立ちます．この式を，Donsker-Varadhan representation*1といい，右辺をDV下限と言います．

$$ \mathbb{D}_{KL}(q || p) = \underset{T: X \to \mathbb{R} }{\rm sup} ~ \mathbb{E}_{q} [T(x)] - \log \left( \mathbb{E}_{p} [ {e}^{T(x)} ] \right) $$

この関係式は，任意の実関数 T による近似で，KL情報量に下限を与えられることを保証しており，かつ一致解の存在を示しています．以下で，簡単な証明を記します．

証明

まず，確率密度 q(x) に対して，近似分布 g(x) を考えます． 近似分布 g(x)は，確率密度 p(x) と T(x) をエネルギー関数とみたときのギブス分布*2によって導かれます． 関数 T: X \to \mathbb{R} は任意の実関数*3です．

$$ g(x) = \frac{{e}^{T(x)}}{ \mathbb{E}_{p}[{e}^{T(x)}] } \cdot p(x) \\ \\ $$

次に， q(x) に対する， p(x) と g(x) の擬距離（KL情報量）を考えます．

$$ \begin{eqnarray} \mathbb{D}_{KL}(q || p) &=& \mathbb{E}_{q} \left[ \log \frac{q(x)}{p(x)} \right] \\ \mathbb{D}_{KL}(q || g) &=& \mathbb{E}_{q} \left[ \log \frac{q(x)}{g(x)} \right] \\ \end{eqnarray} $$

これらの差を計算すると．

$$ \begin{eqnarray} \mathbb{D}_{KL}(q || p) - \mathbb{D}_{KL}(q || g) &=& \mathbb{E}_{q} \left[ \log \frac{g(x)}{p(x)} \right] \\ &=& \mathbb{E}_{q} \left[ \log \frac{\frac{{e}^{T(x)}}{\mathbb{E}_{p}[{e}^{T(x)}]} \cdot p(x)}{p(x)} \right] \\ &=& \mathbb{E}_{q} \left[ \log \frac{{e}^{T(x)}}{\mathbb{E}_{p}[{e}^{T(x)}]} \right] \\ &=& \mathbb{E}_{q} [T(x)] - \log \left( \mathbb{E}_{p} [ {e}^{T(x)} ] \right) &\geq& 0 \end{eqnarray} $$

となり，DV下限が導出されました．つまり，ある関数 Tを用いてDV下限を計算したとき，

$$ \mathbb{D}_{KL}(q || p) = (DV下限) + \mathbb{D}_{KL}(q || g) $$

が成り立つので，誤差項 \mathbb{D}_{KL}(q || g) を考慮すれば，KL情報量 \mathbb{D}_{KL}(q || p) はDV下限で下から測ることができます．

*1:Donsker, M. and Varadhan, S. Asymptotic evaluation of certain markov process expectations for large time, iv. Communications on Pure and Applied Mathematics, 36(2):183?212, 1983.

*2:ボルツマン分布とも呼ばれる． 朱鷺の杜Wiki - "Bolzmann分布"

*3:厳密には，値が発散しないことなどが条件になる．

Numpyでカーネル回帰

Python 統計学 機械学習
f:id:yumaloop:20190426185334p:plain:w500

　カーネル法は，非線形データ解析に対する強力な武器です．ソフトマージンSVM・ガウス過程・クラスタリングなどのアルゴリズムの基本要素として頻出します．このポストでは，カーネル法を使って回帰問題を解く手続きを，Pythonで再現してみました．

　※ なお，カーネル法に関する知識は，以下の本を参考にしています．

カーネル多変量解析―非線形データ解析の新しい展開 (シリーズ確率と情報の科学)

カーネル多変量解析―非線形データ解析の新しい展開 (シリーズ確率と情報の科学)

カーネル法入門―正定値カーネルによるデータ解析 (シリーズ 多変量データの統計科学)

カーネル法入門―正定値カーネルによるデータ解析 (シリーズ 多変量データの統計科学)


カーネル回帰とは？

カーネル関数とグラム行列

n 個のデータサンプル \mathcal{D} = \left\{ x^{(i)}, y^{(i)} \right\} \, (i=1, \cdots n) から，関数 y = f(x)を近似します．回帰モデルはカーネル関数 kとパラメータ {\alpha}_i \, (i=1 \cdots n) を用いて以下の式で表されます．

$$ \hat{y}^{(i)} = \sum_{j=1}^{n} \alpha_j k(x^{(i)}, x^{(j)}) \,\,\, i=1 \cdots n $$

推定値 \hat{y}^{(i)}と真値 y^{(i)} の間の距離を残差(residual)として計算します．データサンプルにモデルをfitさせて，残差の合計(あるいは平均)をモデルの損失関数として導出し，最適なパラメータ {\alpha}_i \, (i=1 \cdots n) を求めます．

$$ \begin{align} residual(y^{(i)}, \hat{y}^{(i)}) &= y^{(i)} - \hat{y}^{(i)} \\ &= y^{(i)} - \sum_{j=1}^{n} \alpha_j k(x^{(i)}, x^{(j)}) \end{align} $$

$$ \begin{align} L(\alpha) &= \frac{1}{n} \sum_{i=1}^{n} {residual(y^{(i)}, \hat{y}^{(i)}) }^{2} \\ &= \frac{1}{n} \sum_{i=1}^{n} { \left( y^{(i)} - \sum_{j=1}^{n} \alpha_j k(x^{(i)}, x^{(j)}) \right) }^{2} \\ &= {({\bf y} - {\bf K} {\bf \alpha})}^{\mathrm{T}} ({\bf y} - {\bf K} {\bf \alpha}) \end{align} $$

$$ where, \,\,\, {\bf K} = \begin{pmatrix} k(x^{(1)}, x^{(1)}) & \cdots & k(x^{(1)}, x^{(n)}) \\ \vdots & \ddots & \vdots \\ k(x^{(n)}, x^{(1)}) & \cdots & k(x^{(n)}, x^{(n)}) \end{pmatrix} $$

{\bf K} はカーネル関数を与えるとデータサンプルから計算させる行列で，Gram行列と呼びます．

勾配降下法でパラメータ探索

パラメータ {\alpha}_i \, (i=1 \cdots n) の探索には，ナイーブな勾配降下法を使います．係数 \gamma は学習率です.

$$ \frac{\partial L(\alpha)}{\partial {\bf \alpha}} = -2 \cdot {\bf K}^{\mathrm{T}} ({\bf y} - {\bf K} {\bf \alpha}) \\ {\alpha}_{new} = {\alpha}_{old} + \gamma \cdot \frac{\partial L(\alpha)}{\partial {\bf \alpha}} \mid_{ \alpha = {\alpha}_{old} } $$

カーネル関数としては，RBF kernel(Gaussian kernel)を使う．

k(x, x') := \exp \left( {\large - \frac{{|| x - x' ||}^2}{2 {\sigma}^{2}} } \right)



カーネル回帰をPythonで実装 (numpy only)

コードは全て下記のリポジトリにあります． github.com

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

# Kernel Function
class RBFkernel():
    def __init__(self, sigma=0.5):
        self.sigma = sigma
        
    def __call__(self, x, y):
        numerator = -1 * np.sum((x - y)**2)
        denominator = 2 * (self.sigma**2)
        return np.exp(numerator / denominator)
    
    def get_params(self):
        return self.sigma
    
    def set_params(self, sigma):
        self.sigma = sigma

# Regression Model
class KernelRegression():
    def __init__(self, kernel):
        self.kernel = kernel
        
    def fit_kernel(self, X, y, lr=0.01, nb_epoch=1000, log_freq=50):
        self.X = X
        self.y = y
        self.n = X.shape[0] # sample size
        self.alpha = np.full(self.n, 1) # param alpha: initialize
        self.gram_matrix = np.zeros((self.n, self.n))
        
        # Gradient Descent Algorithm to optimize alpha
        for epoch in range(nb_epoch):
            
            # Gram Matrix
            for i in range(self.n):
                for j in range(self.n):
                    self.gram_matrix[i][j] = self.kernel(self.X[i], self.X[j])
                    self.loss, self.loss_grad = self.mse(self.X, self.y, self.alpha, self.gram_matrix)
                    self.alpha = self.alpha - lr * self.loss_grad
                    
            if epoch % log_freq == 0:
                print("epoch: {} \t MSE of sample data: {:.4f}".format(epoch, self.loss))
                        
                        
    def mse(self, X, y, alpha, gram_matrix):
        loss = np.dot((y - np.dot(gram_matrix, alpha)), (y - np.dot(gram_matrix, alpha)))
        loss_grad = -2 * np.dot(gram_matrix.T, (y - np.dot(gram_matrix, alpha)))
        return loss, loss_grad
    
    def predict(self, X_new):
        n_new = X_new.shape[0]
        y_new = np.zeros(n_new)
        for i in range(n_new):
            for j in range(self.n):
                y_new[i] += self.alpha[j] * self.kernel(X_new[i], self.X[j])
        return y_new

# Experiment

def actual_function(x):
    return 1.7 * np.sin(2 * x) + np.cos(1.5 * x) + 0.5 * np.cos(0.5 * x) + 0.5 * x  + 0.1

sample_size = 100 # the number of data sample
var_noise = 0.7 # variance of the gaussian noise for samples

# make data sample
x_sample = np.random.rand(sample_size) * 10 - 5
y_sample = actual_function(x_sample) + np.random.normal(0, var_noise, sample_size)

# variables for plot (actual function)
x_plot = np.linspace(-5, 5, 100)
y_plot = actual_function(x_plot)

# plot figure
plt.plot(x_plot, y_plot, color="blue", linestyle="dotted", label="actual function")
plt.scatter(x_sample, y_sample, alpha=0.4, color="blue", label="data sample")
plt.title("Actual function & Data sample (N={})".format(sample_size))
plt.legend(loc="upper left")
plt.xlabel("x")
plt.ylabel("y")
plt.show()
f:id:yumaloop:20190426184220p:plain:w500 
# set kernel
sigma=0.2
kernel = RBFkernel(sigma=sigma)

# generate model
model = KernelRegression(kernel)

# fit data sample for the model
model.fit_kernel(x_sample, y_sample, lr=0.01, nb_epoch=1000, log_freq=100)
  epoch: 0      MSE of sample data: 35.2988
  epoch: 100    MSE of sample data: 30.3570
  epoch: 200    MSE of sample data: 29.4241
  epoch: 300    MSE of sample data: 28.8972
  epoch: 400    MSE of sample data: 28.5597
  epoch: 500    MSE of sample data: 28.3322
  epoch: 600    MSE of sample data: 28.1736
  epoch: 700    MSE of sample data: 28.0598
  epoch: 800    MSE of sample data: 27.9759
  epoch: 900    MSE of sample data: 27.9122

# check Gram Matrix of the model
print(model.gram_matrix)
  array([[1.00000000e+000, 3.24082380e-012, 1.86291046e-092, ...,
        3.45570112e-030, 7.50777061e-016, 6.18611768e-129],
       [3.24082380e-012, 1.00000000e+000, 5.11649994e-039, ...,
        1.78993799e-078, 1.05138357e-053, 1.15421467e-063],
       [1.86291046e-092, 5.11649994e-039, 1.00000000e+000, ...,
        6.88153992e-226, 4.47677881e-182, 8.98951607e-004],
       ...,
       [3.45570112e-030, 1.78993799e-078, 6.88153992e-226, ...,
        1.00000000e+000, 4.28581263e-003, 2.58161981e-281],
       [7.50777061e-016, 1.05138357e-053, 4.47677881e-182, ...,
        4.28581263e-003, 1.00000000e+000, 3.95135557e-232],
       [6.18611768e-129, 1.15421467e-063, 8.98951607e-004, ...,
        2.58161981e-281, 3.95135557e-232, 1.00000000e+000]])

# check loss
print(model.loss)
  12.333081499130776

# array for plot (predicted function)
x_new = np.linspace(-5, 5, 100)
y_new = model.predict(x_new)

 plot result
plt.plot(x_plot, y_plot, color="blue", linestyle="dotted", label="actual function")
plt.scatter(x_sample, y_sample, alpha=0.3, color="blue", label="data sample")
plt.plot(x_new, y_new, color="red", label="predicted function")
plt.title("Kernel Regression \n RBF kernel (sigma={}), sample size ={}".format(sigma, sample_size))
plt.legend(loc="upper left")
plt.xlabel("x")
plt.ylabel("y")
plt.show()
f:id:yumaloop:20190426185334p:plain:w500

AICの導出：平均対数尤度の摂動を近似する

統計学 数学

このポストでは，赤池情報量規準(AIC, Akaike Information Criterion)について，特にその導出過程に留意しつつ解説します．AICは，線形モデル(+ガウスノイズ)のパラメータ選択問題を（必要条件の拘束が大きいものの）発展的に解いた偉大な研究成果であり，また，様々な学習問題において本質的な"汎化"問題を考える上でも非常に示唆的です．AICの導出過程を細かく記述した文献については，論文/書籍があるもののweb上には少ない印象を受けました．そこで，なるべく式展開を詳細しつつ，AICの有名な定義式（下式）が求められるまでの過程を記しておきたいと思います．

$$ \begin{equation} A I C = -2 \sum_{i=1}^{n} ~ \log f(x_i | \hat{\theta}_{MLE}( \boldsymbol{x}^n ) ) + 2 p \end{equation} $$

  • サンプルサイズは nとする．
  • パラメータ \thetaの次元は pとする． \theta \in \Theta \in \mathbb{R}^p
  • 確率変数 X_i，そのサンプル x_iの次元は dとする． X \in \mathbb{R}^d
  • 確率変数 Y_i，そのサンプル y_iの次元は 1とする． Y \in \mathbb{R}^1

情報量規準 (シリーズ・予測と発見の科学)

情報量規準 (シリーズ・予測と発見の科学)

赤池情報量規準AIC―モデリング・予測・知識発見

赤池情報量規準AIC―モデリング・予測・知識発見

1. 確率モデルとKL情報量

未知の確率分布関数 G(x)（=「真の分布」）に従って観測された n個のデータサンプル {\boldsymbol{x}}^n := \{ x_i, \dots, x_n \} を考えます．真の分布 G(x)の近似として我々は確率モデルを F(x) を想定します．分布関数 G(x), F(x)に対応する密度関数*1をそれぞれ f(x), g(x)と定義します．

変数 X の真の分布　 ： G(x), g(x)
変数 X の確率モデル ： F(x), f(x)


このとき，モデル f(x)のよさは「真のモデル g(x)に対する確率分布としての近さ」によって評価できます．AIC(Akaike, 1973)では，分布間の近さを測る尺度として次のKL情報量(Kullback-Leibler, 1951)を採用しています．KL情報量は距離の公理のうち「対称性」以外をみたす疑距離であり， \mathbb{D}_{KL}(G ; F)の値が小さいほどモデル f(x)は g(x)に近いと考えることができます．

$$ \begin{eqnarray} \mathbb{D}_{KL}(G ; F) & = & \mathbb{E}_{G} \left[ \log \frac{G(X)}{F(X)} \right] \\ & = & \int \log \frac{g(x)}{f(x)} ~ dG(x) \\ & = & \int_{- \infty}^{\infty} g(x) \log \frac{g(x)}{f(x)} ~ dx \end{eqnarray} $$

さらに，KL情報量を分解すると，「確率モデル f に依存しない不確実性（変数 X の平均情報量）」と「確率モデル f に依存する不確実性（変数 X のモデル f による平均対数尤度）」に分けることができます．

$$ \begin{eqnarray} \mathbb{D}_{KL}(G ; F) & = & \int_{- \infty}^{\infty} g(x) \log \frac{g(x)}{f(x)} ~ dx \\ & = & \int_{- \infty}^{\infty} g(x) \log g(x) ~ dx - \int_{- \infty}^{\infty} g(x) \log f(x) ~ dx \\ & = & \mathbb{E}_{g} \left[ \log g(x) \right] - \mathbb{E}_{g} \left[ \log f(x) \right] \\ & = & - (X の平均情報量) - (X のモデル f による平均対数尤度) \end{eqnarray} $$

変数 X の平均情報量 \mathbb{E}_{g} \left[ \log g(x) \right] は，確率モデル f の選び方に依らない量であり，データの背後にある現象（変数 X の確率的構造）がもつ不確実性の下限です．すなわち，「モデル f(x)の，真のモデル g(x)に対する確率分布としての近さ」を評価する際には，変数 X の平均対数尤度 \mathbb{E}_{g} \left[ \log f(x) \right] にのみ注目すれば良いことがわかります．

平均対数尤度を最大化するモデル f(x|\theta)　＝　KL情報量 \mathbb{D}_{KL}(g ; f) を最小化するモデル f(x|\theta)


  • なお，KL情報量の詳細については，下記記事で紹介しています． yul.hatenablog.com


2. パラメトリックモデルを考える

さて，多くの確率モデル f(x)では，対象となる変数 xの他に，モデリングを拡張するための媒介変数として「パラメータ \theta」を想定します． パラメータの値を陽に指定できる確率モデル f(x|\theta)を，一般に「パラメトリックモデル」と呼びます．ここからは，確率モデルと行った場合，パラメトリックモデル f(x|\theta)のことを指す事にします．

パラメータ \thetaを中心に，問題を整理してみましょう．

ある変数 X の確率構造 g(x) を捉えるために， p 次元パラメータをもつパラメトリックモデル f(x | \theta ) : \theta \in \Theta \in \mathbb{R}^{p} を想定します．推定に用いるデータサンプル {\boldsymbol{x}}^nを固定すると，モデル f(x | \theta)は \thetaの値によって決定されます．ここではパラメータ \thetaを，最尤推定量 \hat{\theta}_{MLE} で置き換えることによって，確率モデル f(x | \hat{\theta}_{MLE}) を構築します．以下に，よく使われる用語を整理しておきます．尤度(likelihood)とよばれる量は，すべてパラメータ \thetaの関数として考えることができます．

f:id:yumaloop:20190407210252p:plain
  • データサンプル \boldsymbol{x}^n に依存する量（データから計算可能）
    • （対数尤度）　　　 \ell(\theta | \boldsymbol{x}^n) = \log f(\boldsymbol{x}^n | \theta) = \sum_{i=1}^{n} \log f(x_i | \theta)
    • （最大対数尤度）　 \underset{\theta \in \Theta}{\rm max} ~ \ell(\theta | \boldsymbol{x}^n) = \ell(\hat{\theta}_{MLE}(\boldsymbol{x}^n) | \boldsymbol{x}^n)
  • データサンプル \boldsymbol{x}^n に依存しない量（データから計算不可能）
    • （平均対数尤度）　 \mathbb{E}_{g(x)} \left[ \log f(X | \theta) \right] \propto \mathbb{D}_{KL}(g ; f)
    • （KL情報量）　　　 \mathbb{D}_{KL}(g ; f) = \int g(x) \log \frac{g(x)}{f(x)} ~ dx

「モデル選択」の問題（あるいは「バイアス-バリアンス分解」「過学習」「汎化誤差」）とは，結局のところ，「具体的なデータから計算可能な量」から「データから計算不可能な量」を推定する際に生じる"偏り"(=バイアス)をどのようにコントロールするのか，を問うているのです．さらに，モデル選択の問題に，パラメトリックモデルかつ最尤推定という仮定をおけば，これはより具体的に，「対数尤度と平均対数尤度の"ズレ"(=バイアス)を評価して適切に割り引く」ことに他なりません．

平均対数尤度は，未知の関数 g(x)で期待値をとっているためデータから計算不可能な量ですが，「サンプル数が大きい（ n \to \infty）」場合，大数の法則を用いることで，対数尤度から推定することが可能です．AICでは，この関係式をヒントに，バイアスを補正した対数尤度（=平均対数尤度の推定量）を導出します．

$$ \frac{1}{n} \sum_{i=1}^{n} \log f(x_i | \theta) ~~ \underset{p}{\to} ~~ \mathbb{E}_{g(x)} \left[ \log f(X | \theta) \right] ~~~ (n \to \infty) $$

ここまでの流れをアルゴリズム風にまとめると以下のようになります． 特に注意すべきは，手続き(a)，(b)で現れる2つの量，対数尤度と平均対数尤度です．

X_1, \dots, X_n ~ i.i.d. ~ \sim g(x) \\ if ~ X_1 = x_1, \dots, X_n = x_n ~ then, \\ ~~~~~~ (a)~Estimate~the~optimal~params. \\ ~~~~~~~~~~~~ \hat{\theta}_{MLE}(\boldsymbol{x}^n) \gets \underset{\theta \in \Theta}{\rm argmax} ~ \log f(\boldsymbol{x}^n|\theta), \\ ~~~~~~~~~~~~ where ~~~~~~~~~~~~ \boldsymbol{x}^n := \{ x_1, \dots, x_n \} ~ (data~sample) \\ ~~~~~~~~~~~~~~~~~~~~~~~~~~ f(\boldsymbol{x}^n|\theta) := \sum_{i=1}^{n} f(x_i|\theta) \\ ~ \\ ~~~~~~ (b)~Evaluate~the~distance~between~g(x)~and~f \left( x|\hat{\theta}_{MLE}(\boldsymbol{x}^n) \right)~by~g(x). \\ ~~~~~~~~~~~~ \mathbb{D}_{KL}(g ; f) = \int_{- \infty}^{\infty} g(x) \log {\large \frac{g(x)}{f(x|\hat{\theta}_{MLE}(\boldsymbol{x}^n))}} ~ dx \\ ~~~~~~~~~~~~~~~~~~~~~~~~~~~ \propto \int_{- \infty}^{\infty} g(x) - \log f \left( x|\hat{\theta}_{MLE}(\boldsymbol{x}^n) \right) dx \\ ~~~~~~~~~~~~~~~~~~~~~~~~~~~ = \mathbb{E}_{g(x)} \left[ - \log f \left( x|\hat{\theta}_{MLE}(\boldsymbol{x}^n) \right) \right] (平均対数尤度)

3. バイアスの不偏推定量を求める

我々の目標/ゴールは，「 \hat{\theta}_{MLE} におけるモデル f(x|\theta) の平均対数尤度を計算すること」です．下図の白丸はデータから計算可能な（データに依存する）量を表しており， \theta_0 は平均対数尤度を最大化するパラメータです．ただし，データ \boldsymbol{x}^n から \theta_0 を見つけることはできません．AICでは，最尤推定量 {\hat{\theta}}_{MLE} を与えた際のモデル f の対数尤度（=最大対数尤度）ではなく，最尤推定量 \hat{\theta}_{MLE} を与えた際のモデル f の平均対数尤度によって，モデル選択を行います．ここで重要な量は，下図の D で示された部分です．

f:id:yumaloop:20190407210252p:plain

モデル f(x|\theta) に対して，データサンプル \boldsymbol{x}^n を固定して， \theta = \hat{\theta}_{MLE}( \boldsymbol{x}^n) における「対数尤度と平均対数尤度の差 D」を考えます．

$$ \begin{eqnarray} D & := & \left( データサンプル \boldsymbol{x}^n の対数尤度 \right) - \left( n \cdot 変数X の平均対数尤度 \right) \\ & = & \log f(\boldsymbol{x}^n | \hat{\theta}_{MLE}(\boldsymbol{x}^n)) - n \cdot \mathbb{E}_{g} \left[ \log f(X | \hat{\theta}_{MLE}(\boldsymbol{x}^n)) \right] \end{eqnarray} $$

さらに， D はデータサンプル \boldsymbol{x}^n に依存するため，その期待値を考えます． データサンプル \boldsymbol{x}^n は密度関数 g(\boldsymbol{x}^n) := {g(x)}^n にしたがってばらつくことに注意すると，

$$ \begin{eqnarray} b(G) & := & \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ D \right] \\ & = & \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \log f(\boldsymbol{x}^n | \hat{\theta}_{MLE}(\boldsymbol{x}^n)) - n \cdot \mathbb{E}_{g} \left[ \log f(X | \hat{\theta}_{MLE}(\boldsymbol{x}^n)) \right] \right] \\ \end{eqnarray} $$

が定義されます． b(G) はバイアスと呼ばれる量です． b(G) に無理やり意味付けを与えると，「確率モデル f に対する，データサンプル \boldsymbol{x}^n の最大対数尤度 \log f(\boldsymbol{x}^n | \hat{\theta}_{MLE}) の"ばらつき"の期待値」といえます．ここで，以下の関係が成り立つ事に注意してください．

$$ \begin{eqnarray} (最大対数尤度の期待値) + (バイアス) & = & n \cdot (\hat{\theta}_{MLE}における平均対数尤度) \\ \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \log f(\boldsymbol{x}^n | \hat{\theta}_{MLE}) \right] + b(G) & = & n \cdot \mathbb{E}_{g(x)} \left[ \log f(X | \hat{\theta}_{MLE}) \right] \\ \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \log f(\boldsymbol{x}^n | \hat{\theta}_{MLE}) + D \right] & = & n \cdot \mathbb{E}_{g(x)} \left[ \log f(X | \hat{\theta}_{MLE}) \right] \end{eqnarray} $$

3.1 Dを分解する．

\theta = \hat{\theta}_{MLE} における「対数尤度と平均対数尤度の差 D」は， \theta_0 を用いて次のように分解できます．

$$ \begin{eqnarray} D & = & \log f(\boldsymbol{x}^n | \hat{\theta}_{MLE}) - n \cdot \mathbb{E}_{g} \left[ \log f(X | \hat{\theta}_{MLE}) \right] \\ & = & \log f(\boldsymbol{x}^n | \hat{\theta}_{MLE}) - \log f(\boldsymbol{x}^n | \theta_0) \\ & ~ & + \log f(\boldsymbol{x}^n | \theta_0) - n \cdot \mathbb{E}_{g(x)} \left[ \log f(X | \theta_0) \right] \\ & ~ & + n \cdot \mathbb{E}_{g(x)} \left[ \log f(X | \theta_0) \right] - n \cdot \mathbb{E}_{g(x)} \left[ \log f(X | \hat{\theta}_{MLE}) \right] \\ \end{eqnarray} $$

よって，以下のように D_1, D_2, D_3 を定義すると， D = D_1 + D_2 + D_3 が成り立ちます．

$$ \begin{eqnarray} D_1 & = & \log f(\boldsymbol{x}^n | \hat{\theta}_{MLE}) - \log f(\boldsymbol{x}^n | \theta_0) \\ D_2 & = & \log f(\boldsymbol{x}^n | \theta_0) - n \cdot \mathbb{E}_{g(x)} \left[ \log f(X | \theta_0) \right] \\ D_3 & = & n \cdot \mathbb{E}_{g(x)} \left[ \log f(X | \theta_0) \right] - n \cdot \mathbb{E}_{g(x)} \left[ \log f(X | \hat{\theta}_{MLE}) \right] \\ \end{eqnarray} $$

（１） D_1 の期待値を計算する

\theta の関数：対数尤度 \ell(\theta) = \log f(\boldsymbol{x}^n | \theta) を，最尤推定量 [\hat{\theta}_{MLE}] のまわりでTaylor展開すると，

$$ \ell(\theta) \simeq \ell(\hat{\theta}_{MLE}) + { (\theta - \hat{\theta}_{MLE}) }^{\mathrm{T}} \frac{\partial \ell(\theta)}{\partial \theta} {\mid}_{\theta = \hat{\theta}_{MLE}} + \frac{1}{2} { (\theta - \hat{\theta}_{MLE}) }^{\mathrm{T}} \frac{{ \partial}^2 \ell(\theta) }{\partial \theta \partial \theta^\mathrm{T}} {\mid}_{\theta = \hat{\theta}_{MLE}} (\theta - \hat{\theta}_{MLE}) $$

さらに， \theta = \theta_0 を代入すると，

$$ \ell(\theta_0) \simeq \ell(\hat{\theta}_{MLE}) + { (\theta_0 - \hat{\theta}_{MLE}) }^{\mathrm{T}} \frac{\partial \ell(\theta)}{\partial \theta} {\mid}_{\theta = \hat{\theta}_{MLE}} + \frac{1}{2} { (\theta_0 - \hat{\theta}_{MLE}) }^{\mathrm{T}} \frac{{ \partial}^2 \ell(\theta) }{\partial \theta \partial \theta^\mathrm{T}} {\mid}_{\theta = \hat{\theta}_{MLE}} (\theta_0 - \hat{\theta}_{MLE}) $$

ここで，

$$ \begin{eqnarray} \frac{\partial \ell(\theta)}{\partial \theta} {\mid}_{\theta = \hat{\theta}_{MLE}} & = & {\bf 0} \\ \\ \frac{1}{n} \frac{{ \partial}^2 \ell(\theta) }{\partial \theta \partial \theta^\mathrm{T}} {\mid}_{\theta = \hat{\theta}_{MLE}}
& = & \frac{1}{n} \frac{{ \partial}^2 \sum_{i=1}^{n} \log f(x_i | \theta) }{\partial \theta \partial \theta^\mathrm{T}} {\mid}_{\theta = \hat{\theta}_{MLE}} \\ & \underset{p}{\to} & \mathbb{E}_{g(x)} \left[ \frac{ {\partial}^2 \log f(X|\theta)}{\partial \theta \partial \theta^\mathrm{T}} {\mid}_{\theta = \theta_0} \right] = J(\theta_0) ~~~~~~ (n \to \infty) \end{eqnarray} $$

が成り立つから，

$$ \ell(\theta_0) \approx \ell(\hat{\theta}_{MLE}) + \frac{n}{2} { (\theta_0 - \hat{\theta}_{MLE}) }^{\mathrm{T}} J(\theta_0) (\theta_0 - \hat{\theta}_{MLE}) $$

が得られます．よって，

$$ \begin{eqnarray} \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ D_1 \right]
& = & \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \log f(\boldsymbol{x}^n | \hat{\theta}_{MLE}) - \log f(\boldsymbol{x}^n | \theta_0) \right] \\ & = & \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \ell( \hat{\theta}_{MLE} ) - \ell( \theta_0 ) \right] \\ & \approx & \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \frac{n}{2} { (\theta_0 - \hat{\theta}_{MLE}) }^{\mathrm{T}} J(\theta_0) (\theta_0 - \hat{\theta}_{MLE}) \right] \\ & = & \frac{n}{2} \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \mathrm{tr} \left\{ J(\theta_0) (\theta_0 - \hat{\theta}_{MLE}) { (\theta_0 - \hat{\theta}_{MLE}) }^{\mathrm{T}} \right\} \right] \\ & = & \frac{n}{2} \mathrm{tr} \left\{ J(\theta_0) ~ \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ (\theta_0 - \hat{\theta}_{MLE}) { (\theta_0 - \hat{\theta}_{MLE}) }^{\mathrm{T}} \right\} \right] \\ & = & \frac{n}{2} \mathrm{tr} \left\{ J(\theta_0) ~ \frac{1}{n} {J(\theta_0)}^{-1} I(\theta_0) {J(\theta_0)}^{-1} \right\} \\ & = & \frac{1}{2} \mathrm{tr} \left\{ I(\theta_0) {J(\theta_0)}^{-1} \right\} \end{eqnarray} $$

（２） D_2 の期待値を計算する

$$ \begin{eqnarray} \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ D_2 \right] & = & \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \log f(\boldsymbol{x}^n | \theta_0) - n \cdot \mathbb{E}_{g(x)} \left[ \log f(X | \theta_0) \right] \right] \\ & = & \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \log f(\boldsymbol{x}^n | \theta_0) \right] - n \cdot \mathbb{E}_{g(x)} \left[ \log f(X | \theta_0) \right] \\ & = & n \cdot \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \frac{1}{n} \sum_{i=1}^{n} \log f(x_i | \theta_0) \right] - n \cdot \mathbb{E}_{g(x)} \left[ \log f(X | \theta_0) \right] \\ & = & n \cdot 0 = 0 \end{eqnarray} $$

（３） D_3 の期待値を計算する

$$ \begin{eqnarray} \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ D_3 \right] & = & \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ n \cdot \mathbb{E}_{g(x)} \left[ \log f(X | \theta_0) \right] - n \cdot \mathbb{E}_{g(x)} \left[ \log f(X | \hat{\theta}_{MLE}) \right] \right] \\ & = & n \cdot \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \mathbb{E}_{g(x)} \left[ \log f(X | \theta_0) - \log f(X | \hat{\theta}_{MLE}) \right] \right] \\ \end{eqnarray} $$

\theta の関数： \eta(\theta) = \mathbb{E}_{g(x)} \left[ \log f(X | \theta) \right] を， \theta_0 のまわりでTaylor展開すると，

\eta(\theta) \approx \eta(\theta_0) + \sum_{i=1}^{p} (\theta_{i} - \theta_{0i}) {\large \frac{\partial \eta(\theta_0)}{\partial \theta_{i}} } + {\large \frac{1}{2} } \sum_{i=1}^{p} \sum_{j=1}^{p} (\theta_{i} - \theta_{0i})(\theta_{j} - \theta_{0j}) {\large \frac{ {\partial}^{2} \eta(\theta_0)}{\partial \theta_i \partial \theta_j} }


さらに， \theta の任意性から \theta = \hat{\theta}_{MLE} を代入すると，

\eta(\hat{\theta}_{MLE}) \approx \eta(\theta_0) + \sum_{i=1}^{p} (\hat{\theta}_{MLEi} - \theta_{0i}) {\large \frac{\partial \eta(\theta_0)}{\partial \theta_i} } + {\large \frac{1}{2} } \sum_{i=1}^{p} \sum_{j=1}^{p} (\hat{\theta}_{MLEi} - \theta_{0i})(\hat{\theta}_{MLEj} - \theta_{0j}) {\large \frac{ {\partial}^{2} \eta(\theta_0)}{\partial \theta_i \partial \theta_j} }


となります．ここで「確率モデル f(x|\theta) によって，真の分布 g(x) が表現可能である」という仮定をおきます．

$$ \exists \theta_0 \in \Theta, ~ \forall x \in \mathbb{R}^d, ~~~ f(x|\theta_0) = g(x) $$

よって， \theta の関数： \eta(\theta) = \mathbb{E}_{g(x)} \left[ \log f(X | \theta) \right] に， \theta = \theta_0 を代入すると，

$$ \mathbb{E}_{g(x)} \left[ \frac{\partial \log f(X|\theta)}{\partial \theta} \mid_{\theta_0} \right] = \mathbb{E}_{g(x)} \left[ \frac{\partial \log g(X)}{\partial \theta} \right] = \int g(x) \frac{\partial \log g(x)}{\partial \theta} ~ dx = \boldsymbol{0} $$

が成り立つので，Taylor展開の第1項は消えて，

\eta(\hat{\theta}) \approx \eta(\theta_0) - {\large \frac{1}{2}} {(\hat{\theta}_{MLE} - \theta_0)}^{\mathrm{T}} J(\theta_0) (\hat{\theta}_{MLE} - \theta_0)

$$ \mathbb{E}_{g(x)} \left[ \log f(X | \hat{\theta}_{MLE}) \right] \approx \mathbb{E}_{g(x)} \left[ \log f(X | \theta_0 ) \right] - \frac{1}{2} {(\hat{\theta}_{MLE} - \theta_0)}^{\mathrm{T}} J(\theta_0) (\hat{\theta}_{MLE} - \theta_0) $$

が成り立ちます．

$$ \begin{eqnarray} \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ D_3 \right] & = & \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ n \cdot \mathbb{E}_{g(x)} \left[ \log f(X | \theta_0) \right] - n \cdot \mathbb{E}_{g(x)} \left[ \log f(X | \hat{\theta}_{MLE}) \right] \right] \\ & = & n \cdot \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \mathbb{E}_{g(x)} \left[ \log f(X | \theta_0) \right] - \mathbb{E}_{g(x)} \left[ \log f(X | \hat{\theta}_{MLE}) \right] \right] \\ & \approx & n \cdot \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \frac{1}{2} {(\hat{\theta}_{MLE} - \theta_0)}^{\mathrm{T}} J(\theta_0) (\hat{\theta}_{MLE} - \theta_0) \right] \\ & = & \frac{n}{2} \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ {(\hat{\theta}_{MLE} - \theta_0)}^{\mathrm{T}} J(\theta_0) (\hat{\theta}_{MLE} - \theta_0) \right] \\ & = & \frac{n}{2} \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \mathrm{tr} \left\{ J(\theta_0) (\hat{\theta}_{MLE} - \theta_0) {(\hat{\theta}_{MLE} - \theta_0)}^{\mathrm{T}} \right\} \right] \\ & = & \frac{n}{2} \mathrm{tr} \left\{ J(\theta_0) ~ \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ (\hat{\theta}_{MLE} - \theta_0) {(\hat{\theta}_{MLE} - \theta_0)}^{\mathrm{T}} \right] \right\} \\ & = & \frac{n}{2} \mathrm{tr} \left\{ J(\theta_0) ~ \frac{1}{n} {J(\theta_0)}^{-1} I(\theta_0) {J(\theta_0)}^{-1} \right\} \\ & = & \frac{1}{2} \mathrm{tr} \left\{ I(\theta_0) {J(\theta_0)}^{-1} \right\} \end{eqnarray} $$


3.2 バイアスの推定量（Dの漸近推定量）

D_1, D_2, D_3 に関する計算結果をまとめると，バイアス b(G) は結局次のように近似されます．

$$ \begin{eqnarray} b(G) &= & \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ D \right] \\ &= & \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ D_1 + D_2 + D_3 \right] \\ &= & \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ D_1 \right] + \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ D_2 \right] + \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ D_3 \right] \\ &= & \frac{1}{2} \mathrm{tf} \left\{ I(\theta_0) {J(\theta_0)}^{\mathrm{-1}} \right\} + 0 + \frac{1}{2} \mathrm{tf} \left\{ I(\theta_0) {J(\theta_0)}^{\mathrm{-1}} \right\} \\ &= & \mathrm{tr} \left\{ I(\theta_0) {J(\theta_0)}^{\mathrm{-1}} \right\} \end{eqnarray} $$

3.3 2つの重要な行列 I, J

パラメータ \theta を任意の値に固定したとき，確率モデル f(X|\theta) のFisher情報量行列 I(\theta) と，平均対数尤度関数 \mathbb{E}_{g(x)} \left[ \log f(X|\theta) \right] のHesse行列 J(\theta)が定義されます． ここで， \theta = \theta_0 ( \forall x, ~ f(x|\theta) = g(x) ) における I(\theta), J(\theta) は次のように記述されます．

  • 確率モデル f(X|\theta) のFisher情報量行列 I(\theta)

$$ \begin{eqnarray} I(\theta_0) & := & \ \mathbb{E}_{g(x)} \left[ \left( \frac{\partial \log f(X | \theta)}{\partial \theta} \right) \left( \frac{\partial \log f(X | \theta)}{\partial {\theta}^{\mathrm{T}}} \right) \mid_{\theta_0} \right] \\ I(\theta_0)_{ij} & := & - \mathbb{E}_{g(x)} \left[ \left( \frac{\partial \log f(X | \theta)}{\partial \theta_i} \right) \left( \frac{\partial \log f(X | \theta)}{\partial \theta_j} \right) \mid_{\theta_0} \right], ~~~ \forall i, j \in [1, p] \end{eqnarray} $$

  • 平均対数尤度関数 \mathbb{E}_{g(x)} \left[ \log f(X|\theta) \right] のHesse行列 J(\theta)

$$ \begin{eqnarray} J(\theta_0) & := & - \mathbb{E}_{g(x)} \left[ \frac{ {\partial}^{2} \log f( X | \theta) }{\partial \theta \partial {\theta}^{\mathrm{T}}} \mid_{\theta_0} \right] \\ J(\theta_0)_{ij} & := & - \mathbb{E}_{g(x)} \left[ \frac{ {\partial}^{2} \log f( X | \theta) }{\partial \theta_i \partial \theta_j} \mid_{\theta_0} \right], ~~~ \forall i, j \in [1, p] \end{eqnarray} $$

p \times p 行列， I(\theta_0), J(\theta_o) では「微分演算」と「内積演算」の順序が異なることに注意してください．さらに， \theta_0 に対して，

$$ \forall x, ~ f(x|\theta_0) = g(x) ~~~ \Longrightarrow ~~~ I(\theta_0) = J(\theta_0) $$

が成り立ちます．

4.AICの導出

さて，バイアス b(G)の不偏推定量が求められたので，これによってAICを導出しましょう．

目標
データサンプルから求めたパラメータ \theta の最尤推定量 \hat{\theta}_{MLE} を使って求めた確率モデル f(x|{\hat{\theta}}_{MLE}) に対して，その対数尤度 \log f({x}^{n}|\theta) （=最大対数尤度）ではなく，平均対数尤度 n \cdot \mathbb{E}_{g(x)} \left[ \log f(X|{\hat{\theta}}_{MLE})\right] の値によって，評価を与える．

ここで，

$$ \exists \theta_0 \in \Theta \subset \mathbb{R}^p, \forall x, ~~~ f(x|\theta_0) = g(x) ~~~ \cdots ~~~ (仮定*) $$

という仮定をおくと，バイアス b(G)は p \times p 行列 I(\theta_0), J(\theta_0) を用いて

$$ b(G) = \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ D \right] \simeq \mathrm{tr} \left\{ I(\theta_0) {J(\theta_0)}^{\mathrm{-1}} \right\} $$

と近似できます．さらに，仮定 (*) より行列 I(\theta_0) = J(\theta_0) が成り立つから，

$$ \mathrm{tr} \left\{ I(\theta_0) {J(\theta_0)}^{\mathrm{-1}} \right\} = \mathrm{tr} \left\{ I(\theta_0) {I(\theta_0)}^{\mathrm{-1}} \right\} = \mathrm{tr} \left\{ I_p \right\} = p \\ i.e. ~~~ b(G) \simeq p $$

を得ます．よって，対数尤度からバイアス b(G) = p を補正することにより，平均対数尤度の推定量(=AIC)を求めることができます．

$$ \begin{eqnarray} (最大対数尤度の期待値) + (バイアス) & = & n \cdot (\hat{\theta}_{MLE}における平均対数尤度) \\ \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \log f(\boldsymbol{x}^n | \hat{\theta}_{MLE}) \right] + b(G) & = & n \cdot \mathbb{E}_{g(x)} \left[ \log f(X | \hat{\theta}_{MLE}) \right] \\ \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \log f(\boldsymbol{x}^n | \hat{\theta}_{MLE}) + p \right] & \simeq & \mathbb{E}_{g(x)} \left[ n \cdot \log f(X | \hat{\theta}_{MLE}) \right] \\ \mathbb{E}_{g(\boldsymbol{x}^n)} \left[ \sum_{i=1}^{n} \log f(x_i | \hat{\theta}_{MLE}) + p \right] & \simeq & \mathbb{E}_{g(x)} \left[ n \cdot \log f(X | \hat{\theta}_{MLE}) \right] \end{eqnarray} $$

上式の左辺を2倍すれば，AICの定義式が求められます．

$$ \begin{equation} A I C = -2 \sum_{i=1}^{n} \log f(x_i | \hat{\theta}_{MLE}) + 2 p \end{equation} $$

*1:離散変数の場合は密度関数は定義できません．簡単のためここでは連続変数のみを考えます．

PAC学習と計算論的学習理論(Computatinonal Learning Theory)の文献まとめ

機械学習
f:id:yumaloop:20190224225119p:plain


　PAC学習 (Probability Approximately Correct learning) とは、イギリスの理論計算機科学者 Leslie Valiant が1984年に以下の論文で初めて提唱した概念で、計算機科学の分野でそれまで研究されていた一般的な計算アルゴリズムの効率性・複雑性に対して、学習アルゴリズムに関しても同様の議論を行うために定義されたものです。

"A theory of the learnable"
Valiant, L. G. (1984). Communications of the ACM 1984 pp1134-1142.

　Valiant は、統計学の分野である「パターン認識(Pattern recognition)」や「決定理論(Decision theory)」の諸問題を、理論計算機科学の分野である計算複雑性理論(Computational Complexity Theory, CCT)と結びつけることで、学習アルゴリズムの持つ「複雑性」を定義しています。具体的に言うと、計算複雑性理論における「多項式時間で計算可能な解法が存在する問題(クラスP)」の定義と近しい形で、「実現可能な学習アルゴリズム」のクラスを定義しました。やがて、Valiantにより創始された学習アルゴリズムに関する一連の研究分野は計算論的学習理論(Computational Learning Theory, CLT)と呼ばれるようになり、今日に至ります。PAC学習の研究成果としては、例えば機械学習モデルの持つ汎化性能についての上界を与えるものなどがあり、近年ではソフトマージンSVMやDeep Learningの汎化誤差に関して、計算論的学習理論の研究者から、たくさんの関連論文が出ています。

　2019年2月現在、機械学習の隆盛下においても、計算論的学習理論やPAC学習に関する日本語の解説はあまりありませんが、「PAC learning」でGoogle検索すると、Introduction, Tutorioal, Surveyといった名前のつく英語の解説文献がそこそこ見つかります。個人的には、以下の文献がわかりやすかったです。

"Overview of the Probably Approximately Correct (PAC) Learning Framework" (David Haussler, UC Santa Cruz, July 2010)

"PAC Learnability" (Karl Stratos, TTIC, September 2016)

　このポストでは、Valiantが導入した計算論的学習理論における重要な2つの概念"true error(generalization error)", "PAC learnability"の定義を紹介し、参考論文を備忘として留めておきます。

定義1（true error or generalization error）
　学習したい"概念"クラス \mathcal{C} とそれに対応づけられた確率変数の集合 \mathcal{X} に対して、学習アルゴリズム \mathcal{A}: X \in \mathcal{X} \mapsto c(X) \in \mathcal{C} を考える。ただし、 \mathcal{X}に対して定義される確率分布を \mathcal{D} とおく。確率分布 \mathcal{D} に対して独立同分布となる m コのサンプル \left\{ x_1, \dots, x_m \right\} と、それに対応する"概念" \left\{ c(x_1), \dots, c(x_m) \right\} のペアからなる訓練集合 S := { \bigl\{ x_i, c(x_i) \bigr\} }_{i=1}^{m} によって学習を行い仮説 h_{S}: \mathcal{X} \to C を立てる。このとき、仮説 h_{S} の真の誤差(true error)あるいは汎化誤差(generalization error)を次式で定義する。

$$ error(h) := \underset{x ~ \sim~ \mathcal{D}}{Pr} \bigl( h_{S}(x) \neq c(x) \bigr) $$

定義2（PAC learnable）
　"概念"クラス C がPAC学習可能であるとは、以下の条件を満たす学習アルゴリズム \mathcal{A} が存在し、かつ学習に必要な訓練集合の大きさ m:=|S| の下限に対して m \geq poly(1/\varepsilon, 1/\delta, dim(\mathcal{X}), size(c)) という関係を満たす多項式 poly(\cdot) が存在することである。

$$ \forall \varepsilon, \delta \in [0, 1], ~~ \forall m \in \mathbb{N}, ~~ \forall c \in C, ~~ \forall \mathcal{D} ~on~ \mathcal{X}, \\ \underset{S ~ \sim~ \mathcal{D}^{m} \times C^{m}}{Pr} \Bigl( \underset{x ~ \sim~ \mathcal{D}}{Pr} \bigl( h_{S}(x) \neq c \bigr) \leq \varepsilon \Bigr) \geq 1 - \delta $$


※ PAC学習では、ある訓練集合 S に対して、高い確率で「高い予測精度のモデル」を作ることができる学習アルゴリズム \mathcal{A} を考える。"PAC Learnable"の定義は抽象的だが、確率分布によって定まる汎化誤差(true error)を念頭においており、PAC学習の分野の成果は、実際に使われている多くの確率モデル・学習アルゴリズムに対する誤差理論へ適用できる。

※ ある訓練集合 S に対して仮説と学習アルゴリズムの関係は h_{S} \gets \mathcal{A}(S) で与えられることに注意。


　ところで、「学習アルゴリズム A 」という表現は、計算機科学・計算理論の色が根強く反映されていると思います。すなわち、数理統計学(確率＆解析学)のお気持ちとしては、学習は、「確率変数の集合間の写像(関数)を、有限集合から近似する計算操作」として解釈されますが、ここでは近似すべき関数の方が強調されているように感じます。

アラン・チューリングは「計算する」とは何か？を定義し「計算できること/できないこと」に厳密な線引きを与えましたが、当然「学習する」とは何か？にも定義が必要です。計算論的学習理論では、計算の枠組みを拡張することによって、学習を同様のスコープで捉えているように思います。


論文リスト

PAC Learningおよび計算論的理論に関する論文
PAC-Baysian Theory*1に関する論文

参考サイト

以下の記事は、PACを含む計算論的学習理論を概説しており、勉強になります。

qiita.com

*1:PAC LearningとBayse推定を組み合わせた理論